구독상품안내
“가수 비 ‘완벽’ 몸매 공개” “투수 김광현 9이닝 ‘완벽’ 투구”신문에서 흔히 볼 수 있는 기사 제목이다. 여기에는 ‘결점이 없이 완전함’을 뜻하는 말로 ‘완벽’이라는 단어가 사용됐다. 그런데 완벽을 한자로 풀면 ‘완전할 완’(完)에 ‘둥근 옥 벽’(壁)으로 ‘완전한 구슬’이라는 뜻이다. ‘결점이 없다’는 뜻의 말에 왜 ‘구슬’이라는 한자어가 들어갔을까.
구슬(璧)을 완전하게(完) 갖고 돌아오겠습니다!
‘완벽’이라는 단어는 사마천의 ‘사기’(史記) 가운데 ‘인상여열전’(藺相如列傳)에 등장하는 일화에서 유래한다.
중국 춘추전국시대 조나라 혜문왕은 초나라의 보배‘화씨의 구슬’(和氏之璧)을 얻었다. 이 소식을 들은 진나라 소양왕은 혜문왕에게 화씨의 구슬을 자신에게 주면 15개의 성을 주겠다는 제안을 했다. 혜문왕은 고민에 빠졌다.
이 제안을 받아들이면 강대국인 진나라 소양왕이 구슬만 뺐고, 약속대로 성을 주지 않을 것 같기 때문이었다. 하지만 제안을 거절하면 그걸 빌미로 진나라가 전쟁을 일으킬 게 뻔했다.
혜문왕은 대장군‘염파’와 상의해 봤지만 뾰족한 수가 없었다. 그때 한 신하가 자기의 식객인‘인상여’(藺相如)라는 사람을 천거했다. 혜문왕이 인상여를 만나 의견을 묻자 그가 대답했다.
“적당한 사람이 없으면 제가 소양왕을 만나러 가겠습니다. 만약 소양왕이 약속을 지키지 않으면 ‘구슬(璧)을 완전하게(完)’ 갖고 돌아오겠습니다.”
소양왕은 인상여를 믿고 그를 진나라에 보냈다. 인상여는 소양왕에게 화씨의 구슬을 바쳤다. 예상대로 소양왕은 성을 조나라에 내줄 생각이 없었다. 인상여는 꾀를 내어 소양왕에게 말했다.
“사실인즉 그 구슬에는 흠이 있습니다. 제가 알려 드리지요.”
소양왕이 아무런 의심 없이 구슬을 건네자 인상여는 재빨리 뒤로 물러나 기둥에 등을 대고 노한 목소리로 말했다.
“저는 왕께서 성을 떼어줄 생각이 없음을 알고, 꾀를 내어 구슬을 돌려받았습니다. 만약 구슬을 강제로 다시 뺏으려 한다면, 구슬을 기둥에 부딪쳐 부숴 버리겠습니다.”
소양왕은 인상여의 기지와 용기에 감탄해 그를 국빈으로 대우해 조나라로 돌려보냈다. 조나라 혜문왕은 그의 공로를 인정해 인상여를 상대부로 임명했다.
고사에서 ‘완벽’이라는 단어의 의미는 인상여가 임무를 완수하겠다는 의미로 쓰였다. 하지만 여기에는 구슬의 기하학적 모양이 구라는 사실이 ‘결점이 없다’는 의미와 강하게 결부돼 있다.
구슬은 수학적으로 공(ball)을 말한다. 공은 둥근 표면과 그 내부를 모두 포함하는 입체 도형이다. 공에서 특히 둥근 표면만을 구(sphere)라고 하며, 구는 원을 원의 중심을 지나는 축을 따라 회전시켜 얻는다.따라서 구는 어떤 평면으로 잘라도 그 단면은 항상 원이다. 또 구를 중심을 지나는 평면으로 자르면 반지름의 길이가 구의 반지름의 길이와 같은 원이 된다.
원은 중심에서 같은 거리만큼 떨어져 있는 점들의 집합이므로 치우침이 없다. 따라서 고대 그리스 사람들은 원을 ‘완전한 도형’으로 여겼다. 이런 사상은 천체의 모양이나 공전궤도가 원이라고 생각하게 하는 데 영향을 미치기도 했다. 즉 ‘완벽’이라는 단어의 뜻은 원이 완전무결하다는 믿음에서 비롯된 셈이다.
사과와 배가 둥근 이유는?
원과 구와 공은 예로부터 수학자들에게 관심의 대상이었다. 이들 도형을 수식으로 나타내는 방식을 알아보자. 원은 평면상의 한 점에서 일정한 거리에 있는 점들의 집합이다. 이 정의를 이용하면 원의 방정식을 쉽게 유도할 수 있다.원의 중심이 C(a,b)이고 반지름의 길이가 r이라고 하면, 원이란 점 C에서 거리 r만큼 떨어져 있는 점 P(x,y)의 집합이다. 따라서 피타고라스의 정리를 이용하면 원의 방정식 (x-a)2+(y-b)2=r2을 얻을 수 있다.
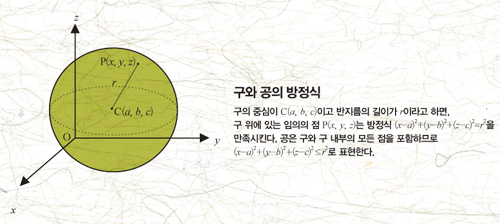
구도 정의로부터 방정식을 유도할 수 있다. 구는 공의 한가운데에서 일정한 거리에 있는 점들의 집합이다. 따라서 구의 중심이 C(a,b,c)이고, 반지름의 길이가 r이라고 하면, 피타고라스의 정리에 따라 구 위에 있는 임의의 점 P(x,y,z)는 다음과 같은 방정식을 만족시킨다.
(x-a)2+(y-b)2+(z-c)2=r2
공은 같은 표면적을 갖는 입체도형 가운데 부피가 가장 크다. 자연계에는 이 사실이 적용된 경우가 많다. 대표적인 예로 과일 대부분이 구 모양을 하고 있다. 사과나 배 같은 과일이 공 모양인 이유는 공이 표면적은 최소이면서 부피는 최대가 되므로 과일은 많은 과육을 가지면서 수분의 증발은 최소화할 수 있기 때문이다.
공의 표면인 구는 일종의 2차원 곡면으로 우리가 발을 딛고 사는 지구의 모양이기도 하다. 지구가 반지름이 약 6500km에 이르는 구라는 사실이 밝혀진 뒤, 사람들은 지구 위의 위치를 표시하는 방법을 만들기 시작했다.
그 방법 가운데 하나가 경위도좌표계다. 지구 위에 있는 한 점 P의 경도는 영국 그리니치천문대를 0°로 기준으로 삼은 본초자오선으로부터 동서방향으로 잰 각이고, 위도는 적도부터 남북방향을 향해 잰 각이다.
예를 들어 우리나라 독도는 동경(본초자오선에서 동쪽으로)이 약 132°, 북위(적도에서 북쪽으로) 약 37°인 곳에 위치한다. 이처럼 곡면 위에 기준선으로부터 떨어진 각으로 위치를 표시하는 좌표를 ‘구면좌표계’라고 한다.
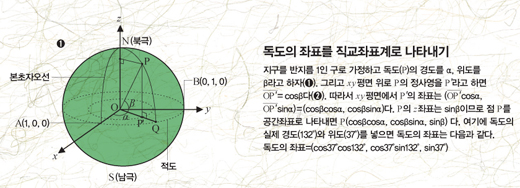
구면좌표계는 지구의 중점 O를 기준으로, 수직하는 직선 x, y, z를 축으로 하는 3차원 공간좌표계로 변환할 수도 있다. 예를 들어 지구를 반지름이 1인 구로 가정하고, 독도의 구면좌표를 P=(α,β)라고 하자. xy 평면 위로 P의 정사영을 P'라고 하면 OP'=cosβ다. 따라서 xy평면에서 P'의 좌표는 (OP'·cosα, OP'·sinα)=(cosβcosα, cosβsinα)다. 한편 P의 z좌표는 sinβ이므로 점 P를 공간좌표로 나타내면 P(cosβcosα, cosβsinα, sinβ)다. 여기에 독도의 실제 동경과 북위 좌표를 넣으면 독도의 좌표는 다음과 같다.
독도의 좌표=(cos37°cos132°, cos37°sin132°, sin37°)
이제 구의 속이 꽉 찬 형태의 입체도형인 공의 방정식을 구해보자. 우리나라 중·고등학교 교육과정에서는 구의 방정식은 다루지만 공의 방정식은 대학 이상 과정에서 다룬다. 공은 구와 구의 내부 공간 모두를 포함하므로 공을 나타낸 식은 부등식의 영역으로 다음과 같이 나타낸다. (x-a)2+(y-b)2+(z-c)2≤r2 또는 이 식을 전개해 정리한 x2+y2+z2+Ax+By+Cz+D≤0꼴로 나타내기도 한다.
구슬에 티가 있으면 ‘하옥’(瑕玉)
구슬이 구의 형태를 지녀 ‘완벽’의 대명사가 된 것과 반대로, 구슬이 흠이 있음을 나타내는 단어에 사용될 경우도 있다. 중국 전한의 회남왕인 유안이 편찬한 철학서 ‘회남자’(淮南子)에는 다음과 같은 글이 실려 있다.
“쥐구멍을 수리하려니 마을 문짝들이 부서지고, 여드름을 문지르니 종기와 등창이 일어난다. 마치 구슬에 흠이 있는 ‘하옥’(瑕玉)과 같아서 그대로 두면 온전하나 없애려면 망가지는 것과 같다.”
여기에 사용된 ‘하옥’이라는 말을 한자로 풀면 ‘티 하’(瑕), ‘구슬 옥’(玉)으로 ‘흠이 있는 옥’이라는 뜻이다. 보통 하옥은 우리말로 ‘옥에 티’라고 표현하며 거의 완벽하지만 아주 티끌만 한 결점이 남아 있다는 뜻으로 쓰인다. 회남자에는 다음과 같은 이야기도 실려 있다.
“반점이 섞여 있는 표범 가죽은 순수한 여우 가죽만 못하다. ‘구슬에 티’(瑕玉)가 있다면 보배라고 할 수 없다. 이는 지극히 순수하기가 어렵다는 것을 나타낸 말이다.”
여기서 보듯 하옥의 원래 의미는 그냥 내버려 두면 좋을 걸 쓸데없는 짓을 해서 화를 자초한다는 뜻이다. 이 밖에 구슬과 관련된 또 다른 고사성어로 ‘옥석혼효(玉石混淆)’라는 말이 있다. ‘옥과 돌이 뒤섞여 있다’는 뜻으로 개탄스러운 세태를 비유하는 말이다.
편집자주
이번 호부터 고사성어에 얽힌 옛 이야기를 수학으로 풀어보는 ‘고사성어 수학교실’ 연재를 시작한다. 한자와 수학의 재미를 한꺼번에 느껴보자.
이광연 교수는 성균관대 수학과를 졸업하고 동대학원에서 석사와 박사학위를 받았다. 그뒤 미국 와이오밍주립대에서 박사후연구원을, 아이오와대에서 방문교수를 지냈다. 현재 한서대 수학과 교수로 재직 중이며, ‘웃기는 수학이지 뭐야’ ‘신화 속 수학이야기’ ‘수학 블로그’ 같은 책을 펴냈다.
