구독상품안내
과학영재학교와 과학고 입시에서 창의적 문제해결력 검사의 비중이 커지고 문제 유형 또한 바뀌고 있다. 출제가능성이 높은 예상문제를 풀어봄으로써 실전감각을 길러두자.
<수학>
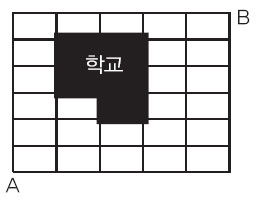1. A에서 출발해 B까지 최단거리로 가는데, 한 칸을 움직이는데 걸리는 시간은 1시간이라고 한다.
1) 학교를 지나지 않고 B까지 가는 방법의 개수는?
2) 학교에서 1시간 이상 머무르는 경우의 개수는?
예시답안
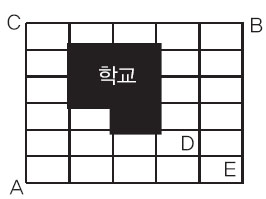1) 그림에서 A에서 B까지 이동하려면 C, D, E 중 한 점을 반드시 거쳐야 한다. 서로 중복되는 경우가 없으므로 경우의 수를 각각 구해 더하면 전체 경우의 수가 나온다.
① C를 거치는 경우 : A~C까지 1가지, C~B까지 1가지이므로 총 1가지다.
② D를 거치는 경우 : A~D까지 5가지, D~B까지 6가지이므로 총 5×6=30가지다.
③ E를 거치는 경우 : A~E까지 1가지, E~B까지 1가지이므로 총 1가지다.
그러므로 학교를 지나지 않고 B까지 가는 방법은 총 32가지다.
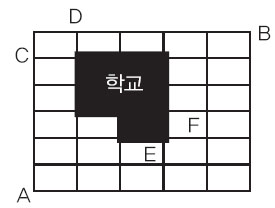2) 학교에서 1시간 이상 머무르는 경우를 직접 구하기 힘들기 때문에 여사건의 경우의 수를 이용한다. 먼저 전체 경우의 수는 총 11번 움직이는데 위로 6번 오른쪽으로 5번 움직이므로 11!/5!6!가지다. 여기서 학교를 지나지 않는 경우와 학교를 지나지만 1시간 이내로 머무르는 경우를 뺀다. 먼저 학교를 지나지 않는 경우는 1)에서 구한 것처럼 32가지다.
그림에서 학교를 지나면서 1시간 이내로 머무르는 경우는 C에서 학교를 거쳐 D로 가는 경우와 E에서 학교를 거쳐 F로 가는 경우뿐이다. 이를 이용해 학교에서 1시간 이내로 머무르는 경우의 수를 구해보자.
① C~학교~D를 거치는 경우 : A~C까지 1가지, C~D까지 1가지, D~B까지 1가지이므로 총 1가지다.
② E~학교~F를 거치는 경우 : A~E까지 4가지, E~F까지 1가지, F~B까지 5가지이므로 총 4×5=20가지다.
두 가지 경우를 모두 합하면 총 21가지다. 그러므로 A에서 B까지 가는 모든 경우의 수 462가지에서 학교를 거치지 않는 경우와 학교에서 1시간 이내로 머무르는 경우를 제외하면 409가지다.
2. 함수 f:R→R이 주어진 조건을 만족할 때 다음 물음에 답하라.
1) f(995)의 값을 구하라.
2) f(84)의 값을 구하라.
1) 995가 1000미만이므로 f(995)는 f(f(1000))과 같다. f(1000)은 997이므로 f(f(1000))=f(997)이다. 다시 997은 1000미만이므로 f(997)=f(f(1002))이고 f(1002)는 999이므로 f(f(1002))=f(999)이다. 999가 여전히 1000미만이므로 f(999)=f(f(1004))이고 f(1004)는 1001이므로 f(f(1004))=f(1001)이다. f(1001)은 998이므로 답은 998이다.
2) 84는 5씩 계속 더해 나갔을 때 1004에서 처음으로 1000을 넘는다. 이때 5를 더하는 회수는 184번이므로 f(84)=f(…f(1004)…)에서 f가 185번 쓰인다. 이 값을 계산하기 위해 f(f(f(f(1004))))를 계산하면 다음과 같다.
f(f(f(f(1004))))=f(f(f(1001)))=f(f(998))=f(f(f(1003)))=f(f(1000))=f(997)
=f(f(1002))=f(999)=f(f(1004))
즉 f(f(…f(1004)…))와 같은 형태의 수에서 f가 4번 이상 쓰이면 이중 2개를 지워도 같은 값을 갖는다. 이를 앞 식에 이용하면 f가 185개이므로 f가 4개 이하일 때까지 2개씩 지워나가면 3개가 남고 f(84)=f(f(f(1004)))이다. f(1004)는 1001이므로 f(84)=f(f(1001))이고 f(1001)은 998이므로 f(84)=f(998)이다. 998은 1000미만이므로 f(84)=f(998)=f(f(1003))이고 f(1003)=1000이므로 f(84)=f(1000)이며 f(1000)은 997이다. 따라서 f(84)=997이다.
<과학>
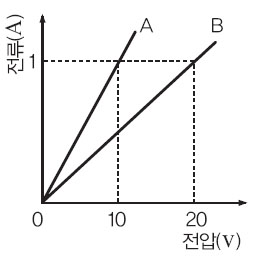1. 다음 그래프는 전구 A와 B에 각각 전원장치를 연결하고 전압을 변화시킬 때, 각각의 전구에 흐르는 전류의 세기를 나타낸 것이다.
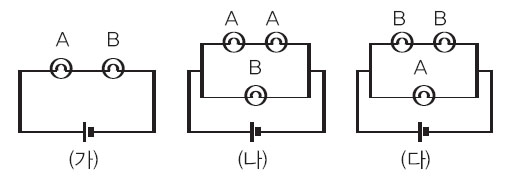
1) 그림 (가)~(다)는 전구 A와 B를 사용해 구성한 회로다. 전체 밝기가 가장 밝은 종류부터 차례대로 말하라(단 각 회로에 걸리는 전압은 같다.).
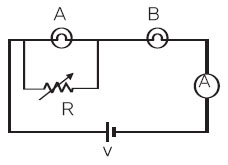2) 오른쪽 그림의 회로는 1)의 회로 (가)에 가변저항 R을 연결한 것이다. R의 저항값을 감소시킬 때 다음 값을 설명하라.
① A에 걸리는 전압 ② 전구 A와 B의 밝기
③ 전류계에 흐르는 전류의 세기
1) 전구의 밝기는 소비전력으로 결정되고 회로 내 각 전구의 소비전력 총합은 전체 회로에서 소비하는 전력 크기와 같다. 이때 전체 회로에서 소비하는 총 전력 PT=ITxVT= V2T/R 이므로 합성저항이 가장 작은 회로에서 전체 밝기가 가장 밝다.
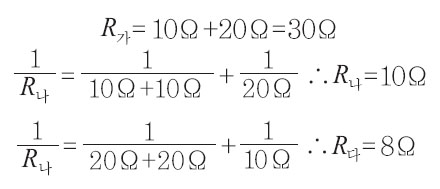
전압의 크기에 따른 전류의 세기를 측정하면 전구 A의 저항 크기 PA=10Ω이고 전구 B의 저항 크기 R B =20Ω이므로 각 회로의 합성저항은 다음과 같다.
따라서 합성저항의 크기가 가장 작은 회로 (다)가 가장 밝고 (나), (가)의 순서로 밝기가 어둡다.
2) 가변저항 R과 전구 A의 합성저항 R t = 10R/(R+10) (∴병렬 연결)이고 전구 B를 포함하는 전체 저항 PT= R t +20이다. 따라서 가변저항 R이 감소할수록 Rt는 점점 줄어들어 0Ω에 가까워지고, RT 또한 점점 감소해 20Ω에 가까워진다.
① 직렬 연결된 두 저항에 걸리는 전압은 각 저항 의 크기에 비례하는데, 가변저항이 감소할수록 전구 B에 대한 R t 의 크기가 0에 가까워지므로 R t 에 걸리는 전압 또한 점점 작아진다. 이때 R t 를 구성하는 가변저항 R과 전구 A는 병렬 연결됐으므로 두 저항에 걸린 전압은 각각 R t 에 걸린 전압과 같다. 따라서 전구 A에 걸린 전압 또한 점점 감소한다.
② 전구의 밝기는 소비전력에 비례하고, 소비전력의 정의와 옴의 법칙을 따르면 전력 P=V2/R 이므로 전압이 점점 감소하는 전구 A의 밝기는 점점 어두워진다. 또 부분합성 저항 RT에 대한 전구 B의 저항 크기비는 증가하므로 전구 B에 걸리는 전압은 점점 증가하며 밝기 또한 점점 밝아진다.
③ 회로에서 전류계는 전체 회로에 흐르는 전류를 측정할 수 있는 위치이고 전압이 일정할 때 전류계에서 측정된 전체 전류의 세기는 합성저항의 크기에 반비례한다. 또 가변저항이 감소함에 따라 회로 전체의 합성저항 RT는 점점 감소한다. 따라서 가변저항이 감소함에 따라 전류계에서 측정된 전류의 세기는 점점 증가한다.
2. 비휘발성, 비전해질 수용액 A와 B를 그림 (가)와 같이 밀폐시켜 놓았더니 그림 (나)와 같이 수면의 변화가 생긴 뒤 더 이상 변화가 없었다.
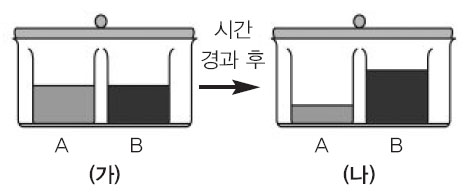
1) 그림 (가)에서 각 용액의 증기압력, 끓는점, 어는점을 각각 비교해 설명하라.
2) 그림 (나)에서 각 용액의 증기압력, 끓는점, 어는점을 각각 비교해 설명하라.
3) 만약 용액 A와 용액 B의 용질을 각각 1g씩 사용하고 물을 100g 사용했다면 분자량은 누가 더 큰지 설명하라.
예시답안
1) 시간이 경과한 뒤 실험 결과로 볼 때 A가 저농도이고 B는 고농도이다. A는 저농도이므로 물입자의 기화를 방해하는 용질입자가 더 적다. 그러므로 증기압력은 A가 B보다 더 크다. 농도가 진할수록 끓는점은 더 증가하고 어는점은 더 감소하므로 A의 끓는점이 B보다 낮고 어는점은 B보다 높다.
2) 그림 (나)에서는 수면의 높이에 더 이상 변화가 없다고 했으므로 두 물질의 농도는 같다. 그러므로 용액 A와 B의 증기압력, 끓는점, 어는점이 서로 모두 같다.
3) 용매와 용질을 같은 양 사용했을 때 용액 A가 저농도이므로 A용질 1g의 몰수가 B용질 1g의 몰수보다 작다. 몰수 = 이므로 몰수가 작으면 분자량이 크다. 그러므로 A용질의 분자량이 B용질보다 크다.
3. 인간은 1번부터 22번까지 염색체를 쌍으로 갖고 추가로 한 쌍의 성염색체를 가지므로 총 염색체 수는 46개다. 이때 성염색체가 XX이면 여성이고 XY이면 남성이다. 다음 물음에 답하라.
1) 만약 ABO 유전자가 X 염색체 내에 있다면 남자가 가질 수 없는 혈액형은 무엇인가?
2) ABO 유전자가 X 성염색체에 있다는 같은 가정 아래 B형 남자와 A형 여자가 결혼해 얻는 아들과 딸의 혈액형은 무엇인가?
3) 인간의 유전자를 조사한 결과 어떤 유전자는 여러 염색체에 중복해 존재한다. 이런 유전자를 중복 유전자라 한다. 유전자 ABO가 성염색체가 아닌 다른 두 염색체에 존재하는 중복 유전자일 때 혈액형 O, A, B, AB형이 될 수 있는 유전자형의 경우의 수를 각각 구하라.
예시답안
1) 유전자가 X 성염색체 내에 있다고 가정했으므로 여자는 A, B, AB, O형 네 가지 혈액형을 모두 갖는다. 하지만 남자는 X 염색체를 하나만 가지므로 A, B, O형은 갖고 AB형은 가질 수 없다.
2) 아들의 경우 아버지는 기여하지 못하므로 아들의 혈액형은 A형이나 O형이다. 딸인 경우는 B형 남자는 우성 B인자만을, 여자는 A 또는 O의 인자를 전달하므로 딸의 혈액형은 AB형 또는 B형이다.
3) 중복 유전자란 하나의 형질을 나타낼 때 둘 이상의 유전자가 서로 협력해 동일한 방향으로 작용하는 유전자다. 서로 다른 두 염색체에 유전자가 중복해 존재하므로 ABO 혈액형을 나타내는 유전자 조합은 네 개의 유전자에서 나타나는 형질이다. 네 개의 유전자가 발현돼 나타나는 유전자 조합은 3×3×3×3=81가지다.
이 중에서 O 유전자는 열성이므로 O형이 나오는 경우는 1가지 즉 OOOO 유전자형이다. A형은 네 개의 유전자 자리에 A 또는 O의 유전자가 들어가야 하므로 2×2×2×2-1(O형)=15가지다. B형도 마찬가지로 15가지다. 따라서 AB형은 81-(15+15+1)=50가지의 유전자 조합이 가능하다.
과제
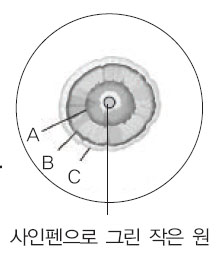그림은 거름종이에 사인펜으로 작은 원을 그린 뒤 원 중앙에 에탄올을 떨어뜨렸을 때 색소 성분 A~C가 분리된 모습을 나타낸 것이다.
1) 실험에서 고정상과 이동상을 각각 말하라.
2) 이동상과의 인력이 가장 큰 물질과 고정상과의 흡착력이 가장 큰 물질을 각각 써라.
3) 실험을 그림처럼 했을 때 그 모양을 그려라.
<수학>
1. A에서 출발해 B까지 최단거리로 가는데, 한 칸을 움직이는데 걸리는 시간은 1시간이라고 한다.1) 학교를 지나지 않고 B까지 가는 방법의 개수는?
2) 학교에서 1시간 이상 머무르는 경우의 개수는?
예시답안
1) 그림에서 A에서 B까지 이동하려면 C, D, E 중 한 점을 반드시 거쳐야 한다. 서로 중복되는 경우가 없으므로 경우의 수를 각각 구해 더하면 전체 경우의 수가 나온다.① C를 거치는 경우 : A~C까지 1가지, C~B까지 1가지이므로 총 1가지다.
② D를 거치는 경우 : A~D까지 5가지, D~B까지 6가지이므로 총 5×6=30가지다.
③ E를 거치는 경우 : A~E까지 1가지, E~B까지 1가지이므로 총 1가지다.
그러므로 학교를 지나지 않고 B까지 가는 방법은 총 32가지다.
2) 학교에서 1시간 이상 머무르는 경우를 직접 구하기 힘들기 때문에 여사건의 경우의 수를 이용한다. 먼저 전체 경우의 수는 총 11번 움직이는데 위로 6번 오른쪽으로 5번 움직이므로 11!/5!6!가지다. 여기서 학교를 지나지 않는 경우와 학교를 지나지만 1시간 이내로 머무르는 경우를 뺀다. 먼저 학교를 지나지 않는 경우는 1)에서 구한 것처럼 32가지다. 그림에서 학교를 지나면서 1시간 이내로 머무르는 경우는 C에서 학교를 거쳐 D로 가는 경우와 E에서 학교를 거쳐 F로 가는 경우뿐이다. 이를 이용해 학교에서 1시간 이내로 머무르는 경우의 수를 구해보자.
① C~학교~D를 거치는 경우 : A~C까지 1가지, C~D까지 1가지, D~B까지 1가지이므로 총 1가지다.
② E~학교~F를 거치는 경우 : A~E까지 4가지, E~F까지 1가지, F~B까지 5가지이므로 총 4×5=20가지다.
두 가지 경우를 모두 합하면 총 21가지다. 그러므로 A에서 B까지 가는 모든 경우의 수 462가지에서 학교를 거치지 않는 경우와 학교에서 1시간 이내로 머무르는 경우를 제외하면 409가지다.
2. 함수 f:R→R이 주어진 조건을 만족할 때 다음 물음에 답하라.
1) f(995)의 값을 구하라.
2) f(84)의 값을 구하라.
1) 995가 1000미만이므로 f(995)는 f(f(1000))과 같다. f(1000)은 997이므로 f(f(1000))=f(997)이다. 다시 997은 1000미만이므로 f(997)=f(f(1002))이고 f(1002)는 999이므로 f(f(1002))=f(999)이다. 999가 여전히 1000미만이므로 f(999)=f(f(1004))이고 f(1004)는 1001이므로 f(f(1004))=f(1001)이다. f(1001)은 998이므로 답은 998이다.
2) 84는 5씩 계속 더해 나갔을 때 1004에서 처음으로 1000을 넘는다. 이때 5를 더하는 회수는 184번이므로 f(84)=f(…f(1004)…)에서 f가 185번 쓰인다. 이 값을 계산하기 위해 f(f(f(f(1004))))를 계산하면 다음과 같다.
f(f(f(f(1004))))=f(f(f(1001)))=f(f(998))=f(f(f(1003)))=f(f(1000))=f(997)
=f(f(1002))=f(999)=f(f(1004))
즉 f(f(…f(1004)…))와 같은 형태의 수에서 f가 4번 이상 쓰이면 이중 2개를 지워도 같은 값을 갖는다. 이를 앞 식에 이용하면 f가 185개이므로 f가 4개 이하일 때까지 2개씩 지워나가면 3개가 남고 f(84)=f(f(f(1004)))이다. f(1004)는 1001이므로 f(84)=f(f(1001))이고 f(1001)은 998이므로 f(84)=f(998)이다. 998은 1000미만이므로 f(84)=f(998)=f(f(1003))이고 f(1003)=1000이므로 f(84)=f(1000)이며 f(1000)은 997이다. 따라서 f(84)=997이다.
<과학>
1. 다음 그래프는 전구 A와 B에 각각 전원장치를 연결하고 전압을 변화시킬 때, 각각의 전구에 흐르는 전류의 세기를 나타낸 것이다. 1) 그림 (가)~(다)는 전구 A와 B를 사용해 구성한 회로다. 전체 밝기가 가장 밝은 종류부터 차례대로 말하라(단 각 회로에 걸리는 전압은 같다.).
2) 오른쪽 그림의 회로는 1)의 회로 (가)에 가변저항 R을 연결한 것이다. R의 저항값을 감소시킬 때 다음 값을 설명하라.① A에 걸리는 전압 ② 전구 A와 B의 밝기
③ 전류계에 흐르는 전류의 세기
1) 전구의 밝기는 소비전력으로 결정되고 회로 내 각 전구의 소비전력 총합은 전체 회로에서 소비하는 전력 크기와 같다. 이때 전체 회로에서 소비하는 총 전력 PT=ITxVT= V2T/R 이므로 합성저항이 가장 작은 회로에서 전체 밝기가 가장 밝다.
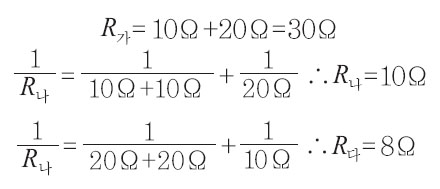
전압의 크기에 따른 전류의 세기를 측정하면 전구 A의 저항 크기 PA=10Ω이고 전구 B의 저항 크기 R B =20Ω이므로 각 회로의 합성저항은 다음과 같다.
따라서 합성저항의 크기가 가장 작은 회로 (다)가 가장 밝고 (나), (가)의 순서로 밝기가 어둡다.
2) 가변저항 R과 전구 A의 합성저항 R t = 10R/(R+10) (∴병렬 연결)이고 전구 B를 포함하는 전체 저항 PT= R t +20이다. 따라서 가변저항 R이 감소할수록 Rt는 점점 줄어들어 0Ω에 가까워지고, RT 또한 점점 감소해 20Ω에 가까워진다.
① 직렬 연결된 두 저항에 걸리는 전압은 각 저항 의 크기에 비례하는데, 가변저항이 감소할수록 전구 B에 대한 R t 의 크기가 0에 가까워지므로 R t 에 걸리는 전압 또한 점점 작아진다. 이때 R t 를 구성하는 가변저항 R과 전구 A는 병렬 연결됐으므로 두 저항에 걸린 전압은 각각 R t 에 걸린 전압과 같다. 따라서 전구 A에 걸린 전압 또한 점점 감소한다.
② 전구의 밝기는 소비전력에 비례하고, 소비전력의 정의와 옴의 법칙을 따르면 전력 P=V2/R 이므로 전압이 점점 감소하는 전구 A의 밝기는 점점 어두워진다. 또 부분합성 저항 RT에 대한 전구 B의 저항 크기비는 증가하므로 전구 B에 걸리는 전압은 점점 증가하며 밝기 또한 점점 밝아진다.
③ 회로에서 전류계는 전체 회로에 흐르는 전류를 측정할 수 있는 위치이고 전압이 일정할 때 전류계에서 측정된 전체 전류의 세기는 합성저항의 크기에 반비례한다. 또 가변저항이 감소함에 따라 회로 전체의 합성저항 RT는 점점 감소한다. 따라서 가변저항이 감소함에 따라 전류계에서 측정된 전류의 세기는 점점 증가한다.
2. 비휘발성, 비전해질 수용액 A와 B를 그림 (가)와 같이 밀폐시켜 놓았더니 그림 (나)와 같이 수면의 변화가 생긴 뒤 더 이상 변화가 없었다.
1) 그림 (가)에서 각 용액의 증기압력, 끓는점, 어는점을 각각 비교해 설명하라.
2) 그림 (나)에서 각 용액의 증기압력, 끓는점, 어는점을 각각 비교해 설명하라.
3) 만약 용액 A와 용액 B의 용질을 각각 1g씩 사용하고 물을 100g 사용했다면 분자량은 누가 더 큰지 설명하라.
예시답안
1) 시간이 경과한 뒤 실험 결과로 볼 때 A가 저농도이고 B는 고농도이다. A는 저농도이므로 물입자의 기화를 방해하는 용질입자가 더 적다. 그러므로 증기압력은 A가 B보다 더 크다. 농도가 진할수록 끓는점은 더 증가하고 어는점은 더 감소하므로 A의 끓는점이 B보다 낮고 어는점은 B보다 높다.
2) 그림 (나)에서는 수면의 높이에 더 이상 변화가 없다고 했으므로 두 물질의 농도는 같다. 그러므로 용액 A와 B의 증기압력, 끓는점, 어는점이 서로 모두 같다.
3) 용매와 용질을 같은 양 사용했을 때 용액 A가 저농도이므로 A용질 1g의 몰수가 B용질 1g의 몰수보다 작다. 몰수 = 이므로 몰수가 작으면 분자량이 크다. 그러므로 A용질의 분자량이 B용질보다 크다.
3. 인간은 1번부터 22번까지 염색체를 쌍으로 갖고 추가로 한 쌍의 성염색체를 가지므로 총 염색체 수는 46개다. 이때 성염색체가 XX이면 여성이고 XY이면 남성이다. 다음 물음에 답하라.
1) 만약 ABO 유전자가 X 염색체 내에 있다면 남자가 가질 수 없는 혈액형은 무엇인가?
2) ABO 유전자가 X 성염색체에 있다는 같은 가정 아래 B형 남자와 A형 여자가 결혼해 얻는 아들과 딸의 혈액형은 무엇인가?
3) 인간의 유전자를 조사한 결과 어떤 유전자는 여러 염색체에 중복해 존재한다. 이런 유전자를 중복 유전자라 한다. 유전자 ABO가 성염색체가 아닌 다른 두 염색체에 존재하는 중복 유전자일 때 혈액형 O, A, B, AB형이 될 수 있는 유전자형의 경우의 수를 각각 구하라.
예시답안
1) 유전자가 X 성염색체 내에 있다고 가정했으므로 여자는 A, B, AB, O형 네 가지 혈액형을 모두 갖는다. 하지만 남자는 X 염색체를 하나만 가지므로 A, B, O형은 갖고 AB형은 가질 수 없다.
2) 아들의 경우 아버지는 기여하지 못하므로 아들의 혈액형은 A형이나 O형이다. 딸인 경우는 B형 남자는 우성 B인자만을, 여자는 A 또는 O의 인자를 전달하므로 딸의 혈액형은 AB형 또는 B형이다.
3) 중복 유전자란 하나의 형질을 나타낼 때 둘 이상의 유전자가 서로 협력해 동일한 방향으로 작용하는 유전자다. 서로 다른 두 염색체에 유전자가 중복해 존재하므로 ABO 혈액형을 나타내는 유전자 조합은 네 개의 유전자에서 나타나는 형질이다. 네 개의 유전자가 발현돼 나타나는 유전자 조합은 3×3×3×3=81가지다.
이 중에서 O 유전자는 열성이므로 O형이 나오는 경우는 1가지 즉 OOOO 유전자형이다. A형은 네 개의 유전자 자리에 A 또는 O의 유전자가 들어가야 하므로 2×2×2×2-1(O형)=15가지다. B형도 마찬가지로 15가지다. 따라서 AB형은 81-(15+15+1)=50가지의 유전자 조합이 가능하다.
과제
그림은 거름종이에 사인펜으로 작은 원을 그린 뒤 원 중앙에 에탄올을 떨어뜨렸을 때 색소 성분 A~C가 분리된 모습을 나타낸 것이다.1) 실험에서 고정상과 이동상을 각각 말하라.
2) 이동상과의 인력이 가장 큰 물질과 고정상과의 흡착력이 가장 큰 물질을 각각 써라.
3) 실험을 그림처럼 했을 때 그 모양을 그려라. 
