d라이브러리

화학나라 초원에는 토끼가 산다. 드넓은 초원에 말뚝 하나가 서 있고 작은 토끼 한 마리가 튼튼한 고무줄에 묶여 있다. 고무줄의 길이는 1km 정도로 아주 길고 말뚝 위에 토끼가 좋아하는 당근이 있다. 토끼는 당근이 있는 말뚝 쪽으로 가려하지만 말뚝에 도착해도 높이 때문에 당근을 먹을 수 없다.

토끼는 그래도 미련을 버리지 못하고 말뚝 주위를 맴돌며 배가 고프면 주위의 풀을 뜯어 먹는다. 말뚝 주위의 풀을 다 먹어 버리면 토끼는 좀 더 멀리 가려 하겠지만 그럴수록 고무줄이 목을 죌 테니 아주 멀리 가지는 못한다.

몇 달이 지난 뒤 비행기를 타고 상공에서 말뚝 주위를 보면, 말뚝을 중심으로 반지름이 고무줄의 길이 정도인 동그란 원을 볼 수 있다. 토끼가 풀을 뜯어 먹은 흔적이다.고무줄 길이보다 더 먼 곳의 풀은 간간히 뜯겨 있고 말뚝에 가까이 갈수록 흔적이 진하다.

풀이 뜯긴 흔적을 보면 토끼가 어디에 오랫동안 있었는지 알 수 있다. 하지만 토끼가 지금 어디에서 어느 방향으로 얼마나 빨리 뛰어 다니고 있는지는 알 수 없다. 토끼를 자세히 보려고 비행기의 높이를 낮추면 토끼는 놀라 그 자리에 조용히 죽은 척하거나 땅을 파고 들어가 숨어버릴지도 모른다.

확률로만 알 수 있는 전자 운동

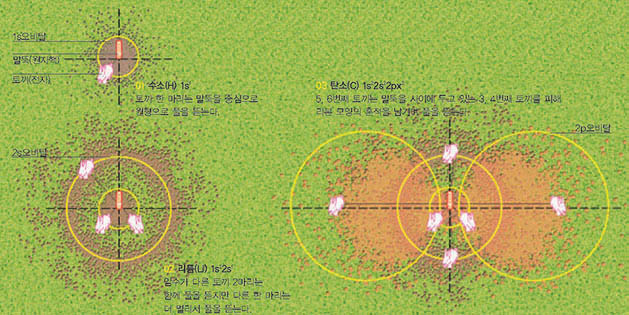
수소(H) 원자를 이루는 전자는 화학나라 토끼와 같다. 음전하인 전자(토끼)는 양전하의 양성자(말뚝 위의 당근)를 좋아하기 때문에 원자 중심에 있는 양성자 주위를 맴돈다. 고무줄에 묶인 토끼처럼 멀리 가는 일은 자주 일어나지 않는다. 게다가 우리는 전자의 움직임을 볼 수 없다. 다만 전자가 양성자를 중심으로 어디에 얼마나 자주 있는지만 알수 있다.

전자가 양성자를 중심으로 90%정도 머무르는 공간을 나타낸 분포도를 ‘오비탈’(orbital)이라고한다. ‘ 궤도’를 뜻하는 ‘orbit’에서 온 말로 토끼가 움직인 길을 알 수 없듯이 전자가 움직인 궤도를 알 수 없기 때문에 붙인 이름이다. 특히 구형 오비탈을 s오비탈이라고 부른다.

이제 토끼를 두 마리 묶어 보자. 처음 토끼가 수컷이면, 암컷 토끼를 데려와 같은 길이의 고무줄로 묶는다. 그러면 둘은 행복하게 풀을 뜯을 것이고 그 흔적도 한 마리만 있을 때와 다를 바가 없다. 마찬가지로 헬륨(He)의 경우 전자 2개가 s오비탈에 어려움 없이 있을 수 있다. 이처럼 오비탈 하나에는 전자 2개만 들어갈 수 있는데, 이를‘파울리의 배타 원리’라고 한다.

하지만 여기에 세 번째 토끼를 묶어 두면 같은 성별의 토끼끼리 싸울 게 분명하다. 어떻게 하면 세 마리 토끼가 매번 싸우지 않고 지내게 할 수 있을까. 세 번째 토끼를 묶는 고무줄의 길이를 더 길게 하면 된다. 그러면 세 번째 토끼는 당근이 먹고 싶어서 말뚝 쪽으로 가겠지만 두 마리가 올 수 없는 영역에서 주로 풀을 뜯을 것이다. 즉 전자가 3개 있는 리튬(Li)은 전자 하나가 1s오비탈 바깥쪽에 있다.

전자 1개 또는 2개가 만드는 오비탈을 1s오비탈, 세 번째 전자가 만드는 오비탈을 2s오비탈이라고 한다. 전자가 어떤 오비탈에 몇 개 있는지는 위첨자로 표시한다. 수소는 1${s}^{1}$, 헬륨은 1${s}^{2}$, 리튬은 1${s}^{2}$2${s}^{1}$, 그리고 베릴륨(Be)은 1${s}^{2}$2${s}^{2}$로 표시하는 식이다.

오비탈 하나에 전자 2개 들어가

토끼 수를 늘려 다섯 마리를 묶어 두면 어떻게 될까. 2s오비탈에 있는 3번째, 4번째 토끼(전자)는 넓은 면적에서 풀을 뜯기 때문에 자기가 먹고 있는 풀만 건드리지 않으면 크게 문제될 게 없다. 따라서 고무줄 길이를 약간만 늘여도 된다. 그러면 5번째 토끼는 말뚝을 사이에 두고 반대편에서 풀을 뜯는 3번째와 4번째 토끼를 피해 리본 모양의 흔적을 남긴다.

원자 세계에서 5번째 전자가 만드는 리본 모양의 오비탈을 p오비탈이라고 한다. 원자 세계는 3차원 공간이므로 2p오비탈은 x, y, z축으로 3개(2px, 2py, 2pz)가 있다.

이제 여기에 전자를 채워보자. 각 오비탈에는 암수 토끼 두 마리, 즉 전자 2개가 존재할 수 있다. 따라서 원자번호 5번인 붕소(B)에서 원자번호 10번인 네온(Ne)까지 전자 배치는 다음과 같다.

B(붕소, 5) : 1${s}^{2}$2${s}^{2}$2${px}^{1}$
C(탄소, 6) : 1${s}^{2}$2${s}^{2}$2${px}^{2}$
N(질소, 7) : 1${s}^{2}$2${s}^{2}$2${px}^{2}$2${py}^{1}$
O(산소, 8) : 1${s}^{2}$2${s}^{2}$2${px}^{2}$2${py}^{2}$
F(불소, 9) : 1${s}^{2}$2${s}^{2}$2${px}^{2}$2${py}^{2}$2${pz}^{1}$
Ne(네온, 10) : 1${s}^{2}$2${s}^{2}$2${px}^{2}$2${py}^{2}$2${pz}^{2}$


토끼 10마리가 풀을 뜯고 있는 곳에 11번째 토끼를 묶으려면, 고무줄의 길이를 많이 늘여서 3s오비탈을 만들어야 한다. 마찬가지로 토끼 2마리가 3s오비탈을 만들면 13번째 토끼부터는 3p오비탈을 만든다. 이런 식으로 18번째 토끼(전자)가 만드는 오비탈을 표시할 수 있다.

예를 들어 원자번호 18번인 아르곤(Ar)인 경우에 전자 배치는 1${s}^{2}$2${s}^{2}$2${px}^{2}$2${py}^{2}$2${pz}^{2}$3${s}^{2}$3${px}^{2}$3${py}^{2}$3${pz}^{2}$이다. 너무 복잡하니까 네온의 전자 배치인 1${s}^{2}$2${s}^{2}$2${px}^{2}$2${py}^{2}$2${pz}^{2}$까지 [Ne]로 표시해 [Ne]3${s}^{2}$3${px}^{2}$3${py}^{2}$3${pz}^{2}$로 간단하게 쓴다.

예를 들면 원자번호 14번인 규소(Si)는 원자번호 10번인 네온보다 전자가 4개 더 많기 때문에 [Ne]3${s}^{2}$3${px}^{2}$로 표시한다. 원자번호 19번인 칼륨(K)의 전자 배치는 [Ne]3${s}^{2}$3${px}^{2}$3${py}^{2}$3${pz}^{2}$4${s}^{1}$이지만 아르곤의 전자 배치를 사용해 [Ar]4${s}^{1}$으로 나타낸다. 마찬가지로 원자번호 20인 칼슘(Ca)의 전자 배치는 [Ar]4${s}^{2}$다.

원소 성질 결정하는 최외각전자

수소(1${s}^{1}$ ), 리튬([H]2${s}^{2}$ ), 나트륨([Ne]3${s}^{1}$ ), 칼륨([Ar]4${s}^{1}$ )의 전자 배치를 살펴보면 공통점이 있다. 맨 마지막 토끼(전자)가 s오비탈에 혼자 존재한다는 점이다. 전자 1개가 s오비탈에 존재하는 다른 원소로는 루비듐(Rb),세슘(Cs), 프랑슘(Fr)이 있는데 이들 원소는 화학적 성질이 아주 비슷하다(수소는 예외).

마찬가지로 s오비탈에 전자 2개가 존재하는 베릴륨, 마그네슘(Mg), 칼륨은 서로 화학적 성질이 비슷하며(헬륨은 예외) 그 성질은 s오비탈에 전자 1개가 존재하는 원소와 다르다.

확률적 개념인 오비탈은 화학나라 전체의 규칙을 정하는 기준이 된다. 자연계에는 서로 다른 109개의 원소가 존재하는데 이들 원소의 화학적 성질은 마지막 오비탈에 존재하는 전자(최외각 전자)의 개수에 크게 좌우된다. 마지막 오비탈이 무엇인지 그리고 그곳에 전자 몇 개가 있는지 알면 비슷한 화학적 성질을 가진 원소끼리 모둠을 만들 수 있다. 화학나라 토끼는 아무런 규칙 없이 들판에 뛰어다니는 것이 아니었다.