d라이브러리

지난해 말 조사에 따르면 한국의 교통사고 발생률은 경제협력개발기구(OECD) 회원국 중 가장 높다고 한다. 반면 승차 중 사망 비율은 가장 낮아 교통사고 치사율은 비교적 낮은 편이라고 하니 그나마 다행한 일이다.

교통사고에서 물리적으로 가장 위험한 상황은 두 차가 정면으로 충돌하는 경우다. 차와 차가 정면충돌할 때는 반발계수가 거의 0에 가까워 이른바 완전비탄성 충돌을 하기 때문에 자동차의 운동에너지 대부분이 자동차를 파손시키는데 사용된다. 완전비탄성 충돌은 진흙덩어리나 껌처럼 충돌 뒤 두 물체가 달라붙는 경우를 말한다. 당연히 이런 사고는 양쪽 운전자 모두에게 치명적이다.

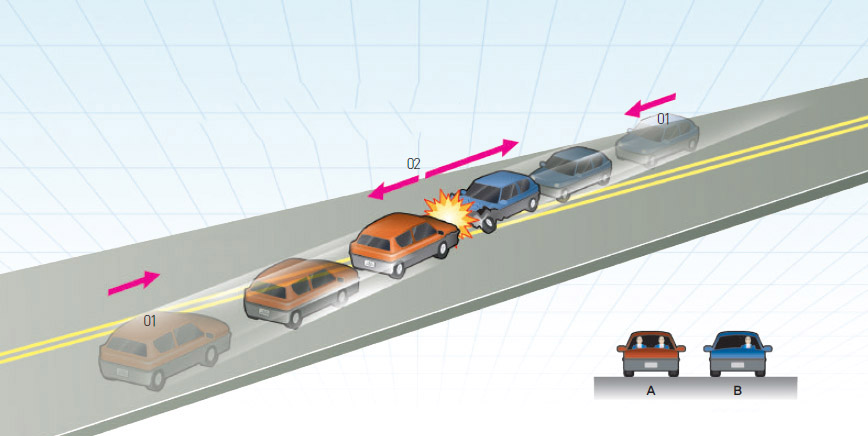
그런데 교통사고 통계자료를 살펴보면 흥미로운 사실이 눈에 띈다. 정면충돌한 경우 운전자 혼자 차에 탔을 때보다 보조석에 사람이 있을 때 운전자의 치사율이 낮다는 것이다. 이유가 뭘까.


총을 어깨에 붙이고 쏘는 이유

상황을 간단히 만들어 생각해 보자. 직선 위에서 똑같은 자동차 2대가 정면으로 부딪쳐 완전비탄성 충돌을 했다. 두 자동차가 충돌하면서 주고받는 힘이 매우 커서 도로와의 마찰력은 무시할 수 있다고 하자.

그러면 두 자동차에 작용하는 힘은 충돌할 때 주고받는 작용-반작용의 힘 한쌍뿐이다. 이 힘은 크기가 같고 방향이 반대이므로 상쇄돼 결국 자동차에 작용하는 알짜힘은 0이다. 이렇게 한 물리계에 작용하는 알짜힘이 0이면 보존되는 양이 있다. 바로 운동량이다.

예를 들어 매끄러운 책상 위에 100원짜리 동전 여러 개를 일렬로 붙여놓는다고 하자. 동전 1개를 이 동전들이 늘어선 방향으로 세게 튕겨 보내면 끝에 있는100원짜리 동전 1개가 바깥으로 튕겨 나간다. 단 세게 튕기는 목적은 동전과 바닥 사이의 마찰력을 무시하기 위해서다.

이런 결과가 나오는 이유는 운동량이 보존되기 때문이다. 일렬로 붙여놓은 동전에 작용하는 알짜힘은 동전끼리 부딪칠 때 전달되는 작용-반작용의 힘이어서 동전 1개를 튕기면 1개가 같은 속도로 튀어나오는 것이다. 만약 일렬로 붙여놓은 동전은 그대로 두고 튕겨 보내는 동전을 2개로 늘리면 어떻게 될까? 운동량 보존 법칙에 따라 끝에 있는 100원짜리 동전 2개가 튕겨 나간다.
 

총을 쏠 때 어깨에 바짝 붙이지 않으면 총알이 발사될 때 총이 몸에 부딪치는 현상도 같은 원리다. 총알이 튀어나갈 때 작용하는 힘은 화약에서 나온다. 총알을 밀어내는 힘이 있으면 반대로 총이 밀려나는 힘도 생긴다. 이 힘 역시 작용-반작용 쌍이므로 총알이 발사될 때 총이 반대방향으로 밀려나 운동량의 합이 0이 되는 것이다. 물론 총이 더 무겁기 때문에 총이 밀려나는 속도는 총알의 속도보다 작다.
이제 자동차 보조석에 사람이 있을 때 치사율이 낮은 이유를 따져 보자.


보조석에 애인을 태우자

운전자를 포함한 자동차 A의 질량 ${m}_{1}$과 자동차 B의 질량 ${m}_{2}$가 모두 1400kg이고, 처음 속도는 시속 90km라고 하자(${v}_{1i}=-{v}_{2 i}=25m/s$). 충돌하는 동안 자동차 A, B가 서로 힘을 가하기 때문에 속도 변화 $Δv$가 생긴다. 그러면 결국 운전자의 치사율은 $Δv$의 크기에 의존하게 된다. 자동차 A와 B가 정면충돌할 때 생긴 속도 변화 $Δ{v}_{1}$과 $Δ{v}_{2}$는 얼마일까?

운동량이 보존되므로 충돌한 뒤 자동차 A, B의 속도를 각각 ${v}_{1f}$, ${v}_{2f}$ 라고 하면 ${m}_{1}{v}_{1}+{m}_{2}{v}_{2}={m}_{1}{v}_{1f} +{m}_{2}{v}_{2f}$다. 완전비탄성 충돌로 충돌 후 두 차가 들러붙어 버리고, 이때 차의 속도를 $V$라고 하면 ${m}_{1}{v}_{1}+{m}_{2}{v}_{2i}=({m}_{1}+{m}_{2})V$다. 따라서

$V = \frac{{m}_{1}{v}_{1i}+{m}_{2}{v}_{2i}} {{m}_{1}+{m}_{2}}$

가 된다. 이 식에 주어진 값을 대입하면 $V=0$이 나온다. 두 자동차의 속도 변화를 계산하면 자동차 A의 경우 $Δ{v}_{1}=V-{v}_{1i} =0-25=-25(m/s)$이고, 자동차 B의경우 $Δ{v}_{2}=V-{v}_{2i} =0-(-25)=25(m/s)$다. 즉 질량이 같은 자동차 2대가 크기가 같고 방향이 반대인 속도로 정면충돌하면 두 차의 속도 변화는 같다.

그렇다면 자동차 A의 보조석에 80kg인 사람이 탔을 때 속도 변화는 어떻게 될까? 이 경우 질량 ${m}_{1}$=1480kg이 되므로 앞의 식에 따라 계산해보면 $V$=0.69(m/s)가 되고, $Δ{v}_{1}$=-24.3(m/s), $Δ{v}_{2}$=25.7(m/s)가 나온다. 즉 보조석에 사람이 타고 있으면 $Δ{v}_{1}$의 크기가 작아진다. 운전자가 사망할 확률은 $Δ{v}_{1}$에 의존하므로 결국 운전자 A의 치사율은 줄어드는 것이다.

사실 정면충돌 통계자료에 $Δv$의 값이 들어있지는 않다. 하지만 $Δv$로 차의 질량과 충돌 사이의 관계를 알 수 있다. 미국의 연구자들이 계산한 결과 운전자 A의 치사위험률 ${r}_{1}$은

${r}_{1} = c{(\frac{{m}_{2}}{{m}_{1}}})^{1.79}$

로 나타난다는 사실이 밝혀졌다(단 c는 상수).

이 식에 따르면 보조석에 사람이 없을 때 운전자 A의 치사위험률은

${r}_{1} = c{(\frac{1400kg}{1400kg})}^{1.79} = c$

이다. 반면 보조석에 사람이 있을 때 운전자 A의 치사 위험률은

${r}_{1}' = c{(\frac{1400kg}{1400kg+80kg})}^{1.79} = 0.905c ≈ 0.91{r}_{1}$

이다. 따라서 운전자 A의 치사위험률은 보조석에 사람이 있을 때 약 9% 줄어든다. 거꾸로 운전자 B의 치사위험률은 그만큼 늘어난다.

한편 운전자의 치사위험률을 나타낸 식에서는 치사위험률이 속도 변화 $Δv$와 관련 없는 것처럼 보인다. 하지만 질량의 비율인 ${m}_{2}/{m}_{1}$은 속도 변화로 바꿔 쓸 수 있다. ${m}_{1} ( {v}_{1f} -{v}_{1i} )=-{m}_{2} ( {v}_{2f} -{v}_{2i} )$ 이고 여기서 ${v}_{1f} -{v}_{1i}=Δ{v}_{1}, {v}_{2f} -{v}_{2i}=Δ{v}_{2}$라고 하면, $\frac{{m}_{2}}{{m}_{1}}$=$\frac {{Δv}_{1i}}{{Δv}_{2}}$ 가 된다. 결국 운전자의 치사위험률은 속도 변화에 의존한다.



무거운 차가 안전한 차

몇 년 전 유행했던 농담 중에‘자동차 티코와 그랜저가 부딪치면 어떻게 될까’라는 얘기가 있었다. 실제로 차량 무게만 놓고 보면 물리적으로 그랜저가 훨씬 안전하다. 운동량이 보존돼 충돌 전후 속도 변화가 질량에 반비례하기 때문이다.

따라서 사람이 많이 탄 차가 사람이 적게 탄 차보다 충돌한 뒤 속도 변화량이 적어 덜 다칠 수 있고, 소형차보다는 질량이 큰 중형차가, 중형차보다는 대형차가 충돌한 뒤 더 안전하다.

간혹 차체가 튼튼하기 때문에 안전하다고 광고하는 경우가 있는데, 충돌했을 때 차체가 찌그러지는 정도는 줄어들겠지만 속도 변화가 줄어드는 것은 아니니 현혹 되지 않기를.

교통선진국인 영국에서는 노면을 사선으로 표시해 도로가 시각적으로 좁다고 느끼게 만들어 운전자가 속도를 줄이도록 유도한다고 한다. 최근 미국에서도 시카고시 당국이 교통사고를 줄이기 위해 커브길에 촘촘히 줄을 긋는 방안을 도입할 계획이라고 밝혔다. 하지만 무엇보다도 중요한 점은 규정 속도를 지키며 안전하게 운전해야 한다는 것이다.