d라이브러리

Q

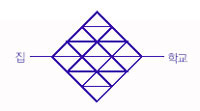
오른쪽 그림은 집에서 학교까지 가는 길을 나타낸 것이다.
집 쪽으로 가는 일 없이 학교를 향해 가는 방법은 몇 가지일까?
 

A

요즘은 좀 덜하지만, 초창기 대학수학능력시험(이하 수능)에는 퍼즐에 가까운 수학 문제가 많이 출제됐다. 대표적인 문제가 격자 모양에서 최단거리로 가는 경로의 수를 세는 것이었다. 이런 문제는 순열과 조합을 이용하면 어렵지 않게 풀린다. 그런데 수능에는 수식만으로 풀기에는 까다로운 문제가 많았다.

이 경우 가장 간단한 방법은 경로를 직접 세어보는 것이다. 경로를 하나씩 찾아가며 세는 것이 아니라 각 분기점마다 경로의 수를 쓰면 문제는 쉽게 풀린다. 순열과 조합으로 계산하는 것보다 훨씬 빠르고 실수할 염려도 적다.

처음에 집을 출발해 첫 번째 갈림길에 도착하는 경우의 수는 당연히 1이다. 여기서 세 갈래 길이 있는데, 다음 갈림길에 도착하는 경우의 수는 각각 1, 3, 1이다(그림 1). 이런 식으로 수를 써넣으면 63이라는 답이 나온다(그림 2).
 

필자가 고등학생 때 이 풀이를 친구들에게 얘기했더니 대부분의 반응이 “그런 짓 왜 해? 그냥 계산하면 되는데?”였다. 실제로 수능 이전에는 거의 모든 문제가 순열과 조합만으로 쉽게 풀리는 것들이었으니 그리 이상한 반응도 아니었다. 교과서는 물론 참고서도 이런 방식을 소개하고 있지 않았다. 그러다 보니 이런 방식의 풀이를 아는 사람이 거의 없어서 수능 초창기에 필자가 ‘잘난 척’ 하는 데 잘 써먹었다.

그런데 이제는 순열과 조합을 이용하는 것보다 위 방법으로 푸는 게 훨씬 일반적인 방법이 됐다. 또 그에 맞게 문제들은 더욱 복잡해졌고. 격세지감이라고나 할까.