d라이브러리

놀이터에서 그네를 타는 어린이는“더 높이 밀어주세요!”하고 조른다. 우리는 어떻게 하면 그네를 더 높이 올라가게 할 수 있는지 경험으로 알고 있다. 그네를 한 번 밀어서 흔든 뒤 그네가 뒤로 왔다가 되돌아가려는 바로 그 순간 밀어준다. 그리고 그네가 멀어졌다가 다시 돌아와 머물렀다가 떠나려는 순간 또 밀어준다. 이렇게 반복하면 그네를 점점 더 높이 올려 보낼 수 있고, 어린이들이 흥분해서 외치는 목소리도 높아진다.

이런 현상은 그네뿐만 아니라 생활에서도 많이 나타난다. 예를 들면 가수 김종서 씨가 KBS 2TV 프로그램‘스펀지’에서 목소리로 와인잔을 깨뜨린 것, 1940년 미국 시애틀 근처 타코마에서 강풍이 불었을 때 다리가 점점 크게 흔들리다가 무너진 것(사진), 1985년 멕시코시티 근처에서 지진이 일어났을 때 20층 높이의 건물만 무너진 것, 다이빙 선수가 다이빙 보드의 진동을 이용해 높이 뛰어오르는 것에도 같은 원리가 작용한다. 이런 현상을 어떻게 설명할 수 있을까.

‘탁!’ 치면 부르르 떤다 !

용수철을 가만히 잡아당기거나 누르면 변형시킨 반대 방향으로 변형된 길이에 비례하는 힘이 작용한다. 식으로는 F=-kx로 쓸 수 있다. 마이너스 부호는 힘의 방향과 늘어난 방향이 반대라는 것을 뜻하고, k는 용수철 상수라고 부르는 양이다.

이 경우 물체의 위치는 x(t)=xsin(wt)로 나타낼 수 있다. 이런 운동의 형태를 단순조화운동이라고 부르고, 이때 w는 각진동수라고 부르는 양이다($w = \sqrt{\frac{k}{m}}$로, 각진동수를 2π로 나누면 1초에 몇 번 진동하는가를 나타 내는 진동수를 얻는다). 즉 용수철이 진동하는 진동수는 관성을 나타내는 용수철의 질량과 탄성을 나타내는 용수철 상수로 표현할 수 있다. 줄에 돌을 매달아 놓은 진자(또는 그네)도 움직이는 각도가 작으면 단순조화운동을 한다. 이때 길이가ℓ인 줄의 각진동수(w)는 $\sqrt{\frac{l}{g}}$다. 여기서 g는 중력가속도(9.8$m/{s}^{2}$)이다.

가시광선 같은 빛에는 전기장과 자기장이 진동하며 앞으로 진행한다. 그래서 빛을 전자기파동이라고 한다. 이처럼 세상에는 진동하는 물체들이 많다. 다른 예를 들어보자. 고체를 살펴보면 고체 안의 원자핵은 일정한 간격으로 배열해 있고, 그 주위에 많은 전자들이 돌아다닌다. 전자들은 전하를 띠고 있으므로 전기적인 힘으로 서로 잡아당기거나 밀고 있다.

입자들이 매우 많아 그 힘을 일일이 계산하기 어렵지만 전체적으로 보면 전자들의 전기적인 힘에 의해 원자핵이 규칙적으로 배열되고, 그 사이에는 마치 용수철이 매달린 것 같은 힘이 작용한다. 따라서 어떤 물체를 당기면 줄어들려고 하고, 누르면 다시 튀어나오는 것이다. 모든 물체는‘탁!’하고 치면 부르르 떤다. 뒤집어 말하면 용수철 탄성력의 근원은 전기적인 힘이다.

물체는 외부에서 충격을 주면 진동한다. 그때 진동수 $f = (2πw)$는 질량과 같이 관성을 나타내는 양, 줄의 장력과 같이 탄성을 나타내는 양에 의해서만 결정된다($f = 2π\sqrt{\frac{k}{m}}$ ). 이를 물체의 고유진동수라고 한다. 물체를 잡아당겼다가 놓으면 이 고유진동수로 진동한다.

물체를 고유진동수와 다른 진동수로 흔들어주면 어떻게 될까. 앞에서 말한 그네를 살펴보자. 눈을 감은 상태에서 그네가 어디 있는지 모르지만 규칙적으로 그네를 밀어준다고 하자. 그러면 그네가 다가올 때 밀어 그네의 속도가 줄어들 수도 있고, 그네가 앞으로 갈 때 밀어 줘 그네의 속도를 더 빠르게 만들 수도 있다. 그네의 진동수와 외부에서 밀어주는 진동수가 다르면 어떤 때는 더 크게 진동할 수도, 다른 때에는 더 작게 진동 할 수도 있다. 시간이 흐르면 그네가 고유진동수로 진동하려는 경향은 결국 사라진다. 그리고 외부에서 진동 시키는 것과 같은 진동수로 움직이는 진동만 남는다. 물론 그 진동의 크기인 진폭은 고유진동수로 진동할 때 보다 일반적으로 작아진다. 이처럼 외부에서 억지로 진동시키는 것을 강제진동이라고 한다.

이제 외부에서 억지로 진동수를 변화시키면서 물체를 진동시켜 보자. 역시 시간이 지나면 외부에서 진동 시키는 진동수대로 진동한다. 하지만 외부진동수가 고유진동수에 가까워지면 그네를 높이 밀어 올릴 때처럼 그네가 앞으로 가려고 할 때 밀어주는 것과 같다. 이 경우 진동하는 진폭이 점점 커진다. 저항이 없으면 이론적으로 진폭이 무한히 커지겠지만 그런 경우는 없다. 하지만 저항이 있더라도 진폭은 매우 커진다. 외부 진동수가 물체의 고유진동수와 비슷해질 때 진동의 폭이 커지는 현상을 공명이라고 한다.

목욕탕 욕조에 누운 뒤 다리를 구부렸다가 몸을 펴면서 등을 욕조의 한 끝으로 밀면 파도가 생긴다. 이 동작을 적당한 진동수로 반복하면 파도는 점점 더 커지다가 욕조 밖으로 넘어간다. 이것도 공명현상이다. 물론 실험하다가 어머니에게 야단맞을 수도 있지만 말이다.

다이빙선수는 공명전문가

와인잔에도 고유진동수가 있다. 그네나 용수철과 달리 와인잔은 곡선 모양 때문에 다양한 형태의 진동이 생길 수 있다. 그 중 한 진동형태는 와인잔의 대칭축을 중심으로 멀어졌다 가까워졌다 하는 진동이다.

물체의 진동수는 물체의 모양에 따라 다르기 때문에 와인잔의 축을 따라 내려오면서 단면을 볼 때 반지름이 다른 부분은 각각 다른 고유진동수를 가지고 있어 고유진동수가 여러 개 생긴다. 이 진동수 중 일부는 소프라노 성악가 목소리의 진동수와 비슷하다(대략 3000~8000Hz). 와인잔이 소프라노 목소리와 공명을 일으키면 잔이 중심축에 대해 벌름거리는 진동이 점점 커지다가 와인잔의 탄성한계를 넘어서면 잔이 깨지게 된다.

비행기 엔지니어들은 날개의 고유진동수를 엔진의 진동수와 다르게 만들기 위해 노력한다. 그렇지 않으면 날개가 엔진 소리와 공명이 일어나 날개가 크게 펄럭거려 상할 수 있고, 심하면 날개가 부러질 수도 있다.

1985년 멕시코시티에서 400km 정도 떨어진 멕시코 서해안에서 지진이 발생해 지진파가 도시까지 밀려왔다. 멀리서 지진이 일어났으므로 지진파의 진폭은 그리 크지 않았다. 이 지진파의 진동수는 약 2초에 한 번이었다. 그런데 높은 건물도 아니고, 낮은 건물도 아닌 20층 안팎의 중간 높이(약 60m) 건물들의 고유진동수가 지진파의 진동수와 비슷했다. 땅이 부드러워 공명이 일어나면서 중간 높이의 건물들은 크게 요동치다가 무너졌다. 그런데 놀랍게도 높은 건물이나 낮은 건물은 멀쩡했다.

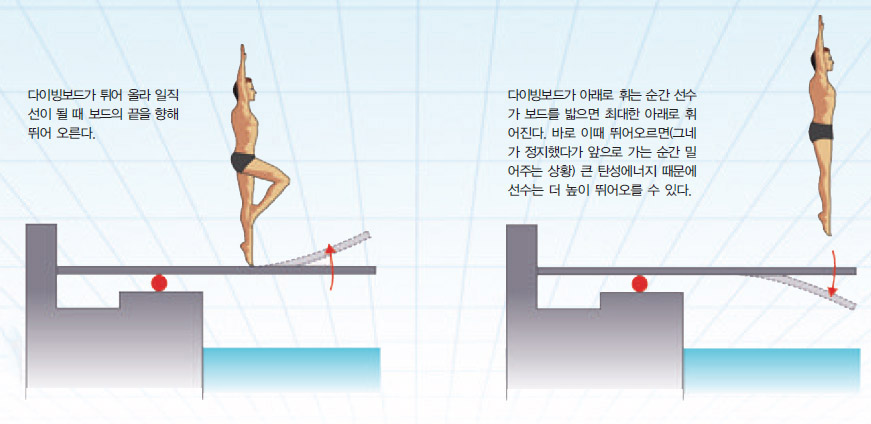
다이빙 선수는 다이빙보드의 탄성을 최대한 이용해 높이 뛰어오르려고 한다. 다이빙보드는 끝에서 약 1/3 되는 지점이 받침점으로 고정돼 있다. 다이빙 선수는 달려가면서 뛰어오르기 전까지 보드를 따라 빠르게 세 걸음을 밟는다. 이때 받침점을 지나면 고정되지 않은 보드의 끝은 아래로 회전한다. 그러면 보드가 튀어 올라 일직선이 될 때 고정되지 않은 보드의 끝을 향해 뛰어 오른다. 유능한 선수는 보드가 2.5번 진동하는 순간 끝점에 다다르도록 훈련한다.

이렇게 하면 다이빙하기 직전 보드를 밟는 순간 보드는 아래쪽으로 가장 큰 속력으로 움직인다. 이때 다이빙 선수가 보드를 밟으면 그네가 정지했다가 앞으로 가는 순간 밀어주는 것처럼 다이빙 보드를 더 누르게 돼 다이빙보드는 최대한 아래로 휘어진다. 그리고 뛰어오르면 다이빙보드의 큰 탄성에너지 때문에 다이빙 선수는 더 높이 뛰어오를 수 있다. 초보선수는 이것을 흉내내지만 대부분 뛰어오르는데 실패한다. 심지어 보드에 부딪치고 떨어지는 경우도 있다.
 

파도소리 만드는 소라껍데기

소라껍데기를 귀에 대면 파도소리 같은 소리가 들린다. 소라가 바다에서 왔기 때문에 바다가 그리워서 내는 소리라고 한다면 멋있게 들릴지 모르지만 과학적으로는 말이 안 되는 이야기다. 소라껍데기는 속이 비어있고 구불구불 꼬여 있으며 속으로 들어갈수록 좁아지는 매우 복잡한 형태를 띠고 있다. 와인잔보다 훨씬 복잡한 모양을 갖고 있는 셈이다. 속이 빈 통은 통 단면의 가로나 세로의 길이에 따라 진동할 수 있는 고유 진동수가 결정된다. 이런 빈 통을 흔히 헬름홀츠 공명기라고 부른다. 소라 껍데기도 이런 공명기이고, 그 모양이 복잡하기 때문에 공명을 일으킬 수 있는 고유진동수가 많다.

이 소라껍데기에 주위의 소리가 들어오면 공명이 일어나는데 여러 진동수의 소리가 모두 공명을 일으키면 소위 백색잡음(모든 종류의 진동수가 골고루 들어있는 잡음)이 들린다. 이 소리가 바로 바람이나 파도소리 같은 진동수 분포를 이루기 때문에 우리는 파도소리가 들린다고 느끼는 것이다.