d라이브러리

Q

어느 회사에 그래픽 디자이너로 근무 중인 유뚱뚱 씨는 최근 살을 빼겠다는 계획을 세웠다. 이것저것 알아보다 ‘동아생식’이란 회사의 생식 다이어트를 하기로 결정했다. 이 다이어트는 15가지 생식 재료를 매일 세 끼씩 닷새 동안 골고루 섭취하는 것으로 총 7회에 걸쳐 35일 동안 진행되는 프로그램이었다. 어떤 두 재료도 같이 먹는 날이 35일 중 2번 이상 나타나지 않도록 하려면 어떻게 일정을 짜야할까?

A

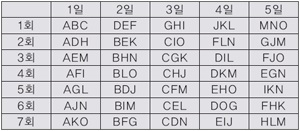
15가지 생식 재료를 A~O로 나타내자. 이제 아래 표와 같이 프로그램을 짜면 5일마다 15가지 재료가 모두 사용되면서, AB, AC, AD, …, NO의 모든 쌍이 꼭 한 번만 나타난다.

이 퍼즐은 영국의 수학자 토마스 페닝턴 커크먼이 1850년 대중 잡지 ‘신사 숙녀의 일지’(Ladies and Gentlemen’s Diary)에 출제했던 것이다. 원래 문제는 15명의 여학생에 대한 것으로, 3명씩 나란히 걸어갈 때 일주일 동안 다른 여학생과 2번 이상 나란히 걷는 일이 없도록 조를 짤 수 있겠냐는 것이었다.
 

커크먼의 여학생 문제는 퍼즐치고는 어려운 편이어서 잡지 독자 가운데 해답을 제시한 사람은 아무도 없었고, 커크먼 본인이 7가지 해답을 모두 제시했다. 이후 많은 수학자들이 이 문제를 연구했고, 몇 년 뒤 ‘스타이너의 삼중 체계’로 일반화됐다. 그리고 이런 구조를 연구하는 분야는 조합론의 큰 주제 가운데 하나인 ‘디자인 이론’으로 발전했다.

커크먼의 문제에서 여학생 수를 더 늘리고 어떤 두 학생과도 꼭 한 번만 나란히 걷도록 제한한 경우는 ‘커크먼의 삼중 체계’로 불린다. 커크먼의 삼중 체계 문제는 한참 동안 풀리지 않고 있다가 문제가 제시된 지 100년도 더 지난 1971년에야 라이-차우두리와 윌슨에 의해 필요충분조건이 증명됐다.

커크먼의 문제는 몇 줄로 나란히 설 것인지의 경우로 바뀌어서도 연구되고 있다. ‘사교 골프 문제’가 그것이다. 주말마다 4명씩 8조로 경기하는 32명의 골퍼들이 같은 조에서 2번 이상 만나는 일이 없도록 하면서 최대한 많은 게임을 하려면 어떻게 일정을 짜야 하겠느냐는 문제로 처음 소개되는 바람에 이런 이름이 붙었다. 현재 가장 좋은 풀이는 9주에 걸쳐 일정을 짜는 것이다. 혹시 10주 이상의 일정을 구성했거나 10주 이상은 불가능하다는 증명에 성공하신 분은 관리자인 워위크 하비(Warwick Harvey)에게 이메일(wharvey @cs.monash.edu.au)을 보내시라.

참, 유 씨는 35일 동안의 괴로움을 잘 견뎌 체중 감량에는 성공했지만, 프로그램이 끝나고 얼마 지나지 않아 스트레스 때문에 다시 살이 찌고 말았다. 하긴 ‘뽀삽질’이 보통 스트레스인가.