d라이브러리

수학에서 골치아픈 문제 중 하나가 부정방정식이다. 방정식보다 미지수의 개수가 많은데 어떻게 풀어야 하나. 또 부정방정식마다 풀이법도 각양각색이다. 동양산학의 원조 구장산술에서는 놀랍게도 부정방정식을 간단한 비례관계로 풀었다.
 

이번 달에 함께 살펴볼 ‘구장산술’의 두번째 장은 ‘속미’(粟米)다. ‘속’은 조, ‘미’는 쌀이니 고대 중국사회의 주무대인 황하유역의 가장 대표적인 두 곡식을 제목으로 삼은 셈인데, 속미 장에는 농산물을 비롯한 여러 종류의 상품을 거래하는 일과 관련된 문제들이 들어있다.

농산물이 아닌 상품은 주로 실, 깃털, 화살대 등인 점을 보면, 활을 제조하기 위한 군수물자 조달과 관계가 있지 않는가 하는 의심이 들기도 한다. 아무튼 이 문제들은 내용적인 측면에서 물물교환과 화폐경제가 공존하던 당시의 시장 모습을 잘 보여준다. 우리가 관심을 갖는 수학적인 측면에서 보면 크게 교환비율과 ‘부정방정식’(indeterminate equations)이 주축을 이루고 있다.

교환비율 문제는 매우 초보적인 비례 계산에 지나지 않으므로 여기서 구태여 장황하게 소개할 필요는 없겠다. 속미 장에 나오는 교환비율 문제 한가지만 예를 들어보자. 문제는 ‘지금 콩 2말이 있는데, 메주로 바꾸려고 한다. 얼마나 얻겠는가?’다. 이에 대한 답은 당시 속미 교환비율에서 콩과 메주의 교환비율이 5 대 7이라는 사실만 알면 쉽게 구할 수 있다. 메주의 양을 x라고 하면 2 : x = 5 : 7이라는 비례식을 만족하므로 메주의 양은
χ =$\frac{24}{5}$ = 2.8(말)
이 된다.

당시의 시장상황에서는 이런 교환비율 문제야말로 가장 일상적으로 행해지던 계산이었다. 하지만 우리의 관심은 이보다 부정방정식에 자연히 집약될 수밖에 없다.

방정식보다 미지수가 많은 문제

서양수학사에서 부정방정식은 기원 후 250년경 알렉산드리아에서 활동했다는 디오판투스(Diophantus of Alexandria)의 ‘산학’(Arithmetica)에서 다뤄진 것을 기원으로 삼고 있다. 이 때문에 부정방정식을 흔히 ‘디오판투스 방정식’(Diophantine equations)이라고 부르기도 한다. 디오판투스의 산학은 원래 13권인데, 이 가운데 오늘날 6권만이 남아있다. 그가 고차방정식의 유리수해까지 구하려고 애쓴 것을 보면, 참으로 대단한 천재였다는 느낌이 든다.

부정방정식은 주어진 방정식보다 미지수의 수가 많아 특정 조건이 주어져야 해결할 수 있는 방정식이다. 물론 부정방정식에 따라 해가 유한개나 무한개, 또는 아예 없을 수도 있다. 예를 들면 방정식 χ² + y² = z²을 만족하는 χ, y, z의 정수, 즉 피타고라스의 수를 구하는 문제가 부정방정식 문제다. 부정방정식의 특징은 통일적인 접근이 곤란하고 개개의 문제에 대해 특수한 해법이 존재한다는 점이다.

고교과정에 등장하는 부정방정식 문제에는 실수 조건이나 정수 조건이 주어진다. 이 가운데 대표격이라면 아무래도 미지수가 2개인 1차 방정식에서 정수해를 구하는 문제가 아닐까 싶다. 이들은 대개 aχ + by = c의 꼴로 주어지는데, 이때 c가 a, b의 최대공약수의 배수이어야만 정수해를 가진다. 자고로 ‘백문이불여일견’(百聞而不如一見)이랬으니, 예제 하나를 들어보자.
문제는 3χ + 9y = 45를 만족시키는 자연수 χ, y를 구하라는 것이다.

이를 풀기 위해 먼저 주어진 식의 양변을 3과 9의 최대공약수인 3으로 나누면, χ + 3y = 15가 된다. 그리고 이것을 x와 y에 대해 정돈하면,

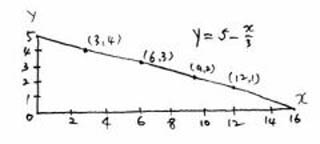
χ = 15 - 3y 이고 y = 5 - $\frac{χ}{3}$
이다. 이들의 범위는 각각 0 <; x <; 15이고 0 <; y <; 5로 드러난다. 이때 y의 범위를 만족시키는 자연수가 1, 2, 3, 4라는 점에 주목해 이에 대응되는 χ값을 알아보면, 결국 다음과 같은 네쌍의 자연수를 얻게 된다. 정답은 y = 1일 때 x = 12, y = 2일 때 x = 9, y = 3일 때 χ = 6, 그리고 y = 4 일 때 χ = 3이다.

그런데 이 문제는 그래프에서 볼 수 있듯이,
y = 5 - $\frac{χ}{3}$
라는 직선 상에 놓여있는 제1사분면의 점 (χ, y)를 찾아보라는 문제로 이해해도 좋겠다.

기율술 대 반기율술

그러면 이제 속미 장의 부정방정식 문제를 직접 살펴보자. 속미 장에는 부정방정식 문제가 모두 아홉개가 들어있다. 이들은 이른바 ‘기율술’(其率術)과 ‘반기율술’(反其率術)이라는 두가지 종류의 산술과 관련된 예제로 분류된다.

기율술은 상급품과 하급품의 단가가 서로 인접한 두 자연수일 때, 각각의 수량과 단가를 구하려는 것이고, 반기율술은 화폐 1단위당 살 수 있는 상급품과 하급품의 수량이 인접한 두 자연수일 때, 각각의 수량과 단가를 알아보려는 것이다. 속미 장에는 기율술 문제가 여섯이고 반기율술 문제가 셋이다. 두 종류의 문제들이 실제로는 거의 대동소이하지만, 어느 한쪽을 젖혀놓았을 때 발생할지 모를 오해의 소지를 피하기 위해 양쪽에서 각각 한개씩 골라 두개만 검토하겠다. 먼저 기율술의 예제부터 살펴보자.

문제 지금 1천1백20전을 내서 실 1섬 2균 18근을 샀다. 상급품과 하급품의 단가가 근당 1전씩 차이가 나는 자연수라면, 각각의 단가와 근수는 얼마인가?
답 단가가 1근에 6전인 상급품은 1섬 10근을, 단가가 1근에 5전인 하급품은 2균 8근을 샀다.

이 문제에서도 드러나듯이 과거의 도량형 단위가 현대인에게는 번잡스럽고 낯설게 느껴지는 것이 사실이다. 그러나 1섬=4균, 1균=30근이라는 점만 알고 나면, 환산하는데 별 어려움은 없다. 즉 문제에서 1섬 2균 18근은 1×4×30 + 2 ×30 + 18 = 198근이다.

그러니 상급품의 근수를 x, 단가를 a라고 하면, 하급품의 근수는 198 - x이고 단가는 a - 1이 된다. 상급품과 하급품 각각의 근수와 단가를 곱하면 각각을 사는데 든 돈이 나오는데, 이들을 합하면 결국 문제에서 주어진 1천1백20전이 된다.

이런 사실을 식으로 표현하면 1120 = xa + (198 - x)(a-1)이고 이를 정리하면 1120 = x + 198(a - 1)이라는 식이 성립된다. 방정식은 하나요 미지수는 둘이니 바로 부정방정식이다. 이것을 풀기 위해서는 문제 속에서 특정한 조건을 찾아내야 한다.

바로 x 와 a는 각각 0 <; x <; 198, a >; 1이라는 조건을 만족시켜야 한다. 이를 이용해 부정방정식을 푼다. a가 1보다 큰 자연수이므로 a를 2부터 식 1120 = x + 198 (a - 1)에 넣어보면 x가 0과 198 사이인 값이 나오게 되는 경우를 찾을 수 있다. 결국 a = 6, x = 130으로 밝혀진다.

이 방법이 번잡하다고 생각하는 사람은 다른 방법을 생각해볼 수 있다. 위에서 정리된 식 1120 = x + 198 (a - 1)을 x에 대해 풀면 x = 1318 - 198a가 된다. 이때 x는 0 <; x <; 198이라는 조건을 만족해야 한다.

따라서 1318 - 198a >; 0이고 1318 - 198a <; 198이다. 이 관계를 정리하면 a<; 6.67이고 a >; 5.66이므로, 이를 만족하는 정수 a는 6이 된다. 또한 x = 130이다. 다시 말하면 상급품의 단가가 1근에 6전이고 근수는 1백30근, 즉 1섬 10근이다.

물론 하급품의 단가는 1근에 5전이고 근수는 68근, 즉 2균 8근에 해당된다.

단서는 서로 인접한 두 자연수

이번에는 반기율술의 예제로 넘어가 보자.

문제 지금 6백20전을 내서 깃털 2천1백개를 샀다. 상급품보다 하급품을 1전에 1개씩 더 준다면, 각각의 값과 수량은 얼마인가?
답 3개에 1전인 상급품은 1천1백40개를, 4개에 1전인 하급품은 9백60개를 샀다.

상급품을 사는데 지출한 금액을 x, 1전으로 살 수 있는 상급품의 수량을 a 개라고 하면, 하급품을 사는데 지출한 금액은 620 - x, 1전으로 살 수 있는 하급품의 수량은 a + 1개가 된다. 상급품과 하급품을 사는데 든 돈과, 1전으로 살 수 있는 수량을 각각 곱하면 각각의 제품을 산 수량이 나오는데, 이들을 더하면 결국 문제에서 주어진 깃털의 총 개수가 된다.

이를 식으로 표현하면 2100 = ax + (a + 1)(620 - x) = 620(a + 1) - x라는 관계가 성립된다. 이때 0 <; x<; 620이고 a는 1보다 큰 자연수다. 이것은 앞에서 다뤘던 기율술 문제의 부정방정식과 같은 꼴이다. 역시 두가지 해법을 생각해볼 수 있다.

먼저 a는 1보다 큰 자연수이므로 2부터 차례로 2100 = 620(a + 1) - x라는 식에 넣어보면 0과 620 사이에 해당하는 x를 찾을 수 있다. 결국 a = 3, x = 380이 된다.

a와 x를 구하는 또다른 방법은 식 2100 = 620(a + 1) - x로부터 정리한 x = 620a - 1480을 이용하는 것이다. 이때 x는 0 <; x <; 620이라는 관계를 만족해야 한다. 따라서 620a - 1480 >; 0이고 620a - 1480 <; 620이다. 이것을 정리하면 a >; 2.39이고 a <; 3.39이다. 이 범위를 만족시키는 자연수 a는 3뿐이다. 그리고 x = 380이다. 즉 상급품은 1전에 3개를 살 수 있고 문제의 수량을 사는데 380전을 지불했다.

이로부터 1전에 3개를 살 수 있는 상급품의 수량이 3× 380 = 1140개라는 사실을 알 수 있다. 반면 하급품은 1전에 4개를 살 수 있고 이렇게 산 하급품의 수량은 4× (620 - 380) = 4 × 240 = 960개라는 것을 구할 수 있다.

가격 차이와 수량은 서로 반비례

그런데 이들 문제에 대해서 구장산술의 풀이법에는 앞에서 살펴본 풀이와 사뭇 다른 접근법을 적용하고 있다. 번거로움을 피하기 위해 앞의 기율술 문제를 예로 들어보자.

그 접근법의 출발점은 실의 평균가격인 1120/198이 5와 6 사이에 놓여 있다는 점에 착안한 것이다. 이때 상급품과 하급품의 단가 차이가 1전이므로, 당연히 상급품의 단가는 6전이고, 하급품의 단가는 5전이라는 해를 바로 구할 수 있다. 그러면 상급품을 구매해 평균가격을 상회하게 된 금액은 하급품을 구매해 평균가격을 밑돌게 된 금액과 정확히 같게 된다. 따라서

(6 - $\frac{1120}{198}$)x = ($\frac{1120}{198}$ - 5)(198 - x)
라는 식이 성립되겠다. 왜냐하면 가격 차이와 수량이 서로 반비례의 관계에 있기 때문이다. 이 식을 풀면 상급품의 근수 x = 130이라는 결과를 앞서의 경우보다도 훨씬 수월하게 구할 수 있다.

놀랍게도 이 방법이 바로 기율술이니 반기율술이니 하는 구장산술의 풀이법인 것이다. 구장산술이 부정방정식 문제를 제시하고도 답을 구하기 위해 비례를 이용한 계산법으로 대처했다고 여겨지는 대목이다.

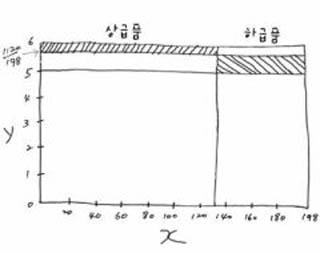
이런 풀이법을 기하적으로 살펴보자. 편의상 그림과 같이 x축을 근수, y축을 단가로 삼아서 왼쪽에 상급품, 오른쪽에 하급품에 지출한 금액을 직사각형의 넓이로 표시할 수 있다.

이때 네 꼭지점이 (0, 1120/198), (0, 6), (130, 1120/198), (130, 6)인 직사각형과 (130, 5), (130, 1120/198), (198, 5), (198, 1120/198)인 직사각형의 넓이가 서로 일치해야 한다는 사실을 뜻한다고 볼 수 있겠다.

사실 또다른 종류의 부정방정식 문제가 구장산술 여덟번째 장인‘방정’장에도 나와 있다. 어쩌면 방정 장의 부정방정식 문제들이 더 재미있고 수준 높을지 모르겠다.

​