d라이브러리

지금으로부터 1천7백여년 전 동양에도 피타고라스정리에 해당하는 구고술이라 불리는 수학원리가 있었다. 또한 동양수학고전에는 수학문제를 실생활에서 찾고 노래로 접하게 하는 친숙함이 깃들어 있다. 동양수학 최고 고전이며 우리민족 수학의 뿌리이기도 한 구장산술을 만나보자.

수학하면 우리는 제일 먼저 서양의 수학과 수학자를 떠올린다. 피타고라스정리로 유명한 피타고라스가 그렇고 기하학의 원전인 ‘기하원본’을 쓴 유클리드가 그렇다. 과연 서양의 수학이 뛰어나 동양의 것은 비교도 되지 않을까. 동양수학은 낯설기도 하지만 그만큼 우리는 이에 대해 아는 바가 없다.

흥미롭게 고대 동양에도 서양에 못지 않은 수학이 있었다. 서양의 피타고라스정리에 해당하는 수학적 원리가 동양수학(산학)에서는 ‘구고술’이라는 이름으로 등장한다. 또 서양수학에 유클리드의 기하원본에 견줄 정도로 막강한 고전이 동양산학에도 있다. 이름하여 ‘구장산술’이 그것이다.

동양산학 최고의 고전인 구장산술은 중국 산학의 효시로 그후의 발달을 결정지었다고 해도 과언이 아니다. 뿐만 아니라 우리나라, 일본, 베트남은 물론 심지어 중국과 쌍벽을 이루는 수학을 발달시킨 인도에도 커다란 영향을 미쳤다.

또 놀랍게도 동양 고대수학서인 구장산술의 내용이 중·고교 교육과정과 상당히 일치할 뿐 아니라 그것을 능가하기까지 한다. 동양수학의 고전 구장산술을 통해 우리수학의 뿌리를 찾고 나아가 교과서수학을 공부하는데 새로운 깊이와 자극을 느낄 수 있으리라 믿어 의심치 않는다.
 

컴퍼스와 자를 손에 든 통치자

우리와 구장산술의 인연은 이미 7-8세기경으로 올라간다. 신라의 국학에서 “산학박사 또는 조교 1인을 가려 철경, 삼개, 구장, 육장을 교재로 삼아 학생들을 가르쳤다”는 ‘삼국사기’의 기록이 남아있을 정도다. 기록 속에 열거된 수학서들 가운데 ‘구장’이 바로 구장산술임은 물론이다. 또한 ‘고려사’에는 당시의 경제관료인 산사(算士)들을 선발하는 시험에서 구장산술의 일부를 선택해 암송시켰다고 적고 있다. 그리고 조선시대 말 정치가이자 산학자였던 남병길(南秉吉, 1820-1869)이 구장산술의 주해서인 ‘구장술해’를 지은 사실은 이 책의 가치가 그때까지도 중시되고 있었음을 말해준다. 이를 종합해보면 구장산술이 근대화·서구화의 소용돌이에 휩쓸렸던 지난 한세기를 제외하고, 1천년이 훨씬 넘도록 우리민족의 수학적 사고와 사회생활, 그리고 더 나아가 문화 전반을 지배해 왔음을 알 수 있다.

구장산술은 263년 위나라의 유휘(劉徽, ?-?)가 편찬하고 주를 붙이면서 현재와 같은 모습을 갖추게 됐다. 비록 3세기에 와서 정착됐다고는 하지만, 그가 쓴 서문에서 주장하는 바에 따르면, 구장산술의 기원은 기원전 27세기경 지혜의 제왕인 황제나 주나라 초기(기원전 12세기)의 정치가 주공을 훨씬 넘어 중국 상고시대 최초의 통치자로 알려진 복희씨까지 거슬러 올라간다고 한다. 다시 말해 이 책은 그 이전에도 얼마나 오랜 세월 동안 발전과 전승을 거듭한 끝에 이뤄진 산물인지 모른다는 말이다. 물론 사람에 따라서는 혹시 그들의 권위를 빌어 산학의 중요성을 부각시키려 한 게 아닐까 하고 의심해볼 수도 있다. 그러나 사실상 이 글은 ‘주역’ 계사전에도 나오는 내용이어서 한갓 야심에 찬 수학자의 뻥튀기로 치부하기만은 어렵다.

한대에서 당대로 이어지는 시기의 중국 무덤 그림 가운데 자주 등장하는 복희씨와 그의 배필인 여와의 모습을 보면, 각각 기역(ㄱ)자 자와 컴퍼스를 무슨 왕홀이나 되는 양 의기양양하게 쳐들고 있다. 영락없이 그들의 지배 기초가 수학에 관한 지식이라는 것을 보여주는 형상이다. 그렇다면 구장산술은 나름대로 동양 고대문명의 비밀을 간직하고 있는 보물창고로 볼 수 있다. 특히 수학이 어떻게 형성됐는지를 가장 잘 알려줄 수 있다고 기대해도 좋겠다.
 

노래로 배우는 산학

필자가 처음 접한 산학서인 16세기 중국산학가 정대위의 ‘산법통종’에 소개된 문제들을 통해 동양산학서에서 어떤 방식으로 산학을 가르쳤는지를 살펴볼 수 있다. 예를 들어 ‘그릇으로 스님 수를 알아 맞추는 노래’(以碗知僧歌)를 보자.

높디높은 산 속에 오래된 절이 있는데,
절 안에 스님들은 몇분인지 모르겠네.
그릇은 모두 3백64개로서
딱 맞게 다 쓰시면서 다툼이 없는데,
셋이서 밥 한그릇을 함께 잡수시며
넷이서 국 한사발을 같이 드신다네.
선생께서는 산술에 능하시다니 묻겠노라.
도무지 절 안에 스님이 몇분이나 계시는가?

답: 6백24명, 밥그릇 2백8개, 국그릇 1백56개.

이 문제는 승려 수를 x라고 놓으면 밥그릇 수는 $\frac{χ}{3}$이고 국그릇 수는 $\frac{χ}{4}$가 될 것이므로, 결국
$\frac{χ}{3}$ +$\frac{χ}{4}$ = $\frac{7χ}{12}$ = 364

라는 식을 풀라는 것이 요점이다. 산법통종의 많은 문제들이 대개 이런 식이다. 특징적인 점을 정리해보면 다음과 같다.

첫째 한문문제를 방정식으로 풀 수 있다는 사실이 매우 새롭다. 방정식은 서양에만 있는 개념이 아니라 동양산학에서도 흔히 등장하는 개념이었던 것이다. 둘째 수학문제에 엉뚱하게도 금욕주의적 승단 생활이 등장하는 점도 재미있다. 동양산학에서는 수학문제를 제시하는데 있어서 추상적이기보다 구체적인 상황을 제시했다. 이렇게 함으로써 수학문제에 좀더 친숙해질 수 있게 했고 실생활문제에서 해결책을 찾을 수 있도록 배려했다.

셋째 산법통종의 위 수학문제는 사실 매행이 일곱개의 한자로 이뤄지고 운율이 맞는 ‘칠언율시’라는 형식으로 구성돼 있다. 이런 형식 속에는 수학이라는 딱딱한 내용을 벗어나 학습자가 쉽고 재미있게 배울 수 있도록 학습의욕을 고취시키기 위한 교수법의 개선 노력도 엿볼 수 있다. 지금으로 말하면 유행가 가사를 수학문제로 바꿔 부른 것이라고 할 수 있는데 참으로 신선한 방법이라 여겨진다.

고대 현실문제의 수리적 해법

구장산술은 산법통종보다 훨씬 이전에 나왔지만 그 내용에 있어서 다양한 분야의 수학문제를 다룰 뿐만 아니라 수학의 원리적인 측면을 잘 다루고 있다. 제목 자체에서 알 수 있듯이 9개의 장으로 이뤄져 있으며, 모두 2백46개의 문제가 등장하고 본문은 기본적으로 문, 답, 풀이의 3중 구조로 돼 있다.

첫째 장 ‘방전’(方田)은 다양한 형태에 관한 평면기하문제와 아울러 분수계산을 취급한 것이다. 둘째 장 ‘속미’(粟米)는 농산품간의 교환비율을 이용해서 교환량을 계산하는 문제가 주종을 이룬다. 셋째 장 ‘쇠분’(衰分)은 차등적인 비율에 따른 할당량을 구하는 문제와 등차급수나 등비급수 문제를, 넷째 장 ‘소광’(少廣)은 $\sum _{n=1} ^{N} \frac{1}{n}$이 관련된 문제와 제곱근이나 세제곱근을 구하는 문제를 각각 취급한다. 다섯째 장인 ‘상공’(商功)에는 토목공사 관련문제와 다양한 형태의 입체에 관한 문제가 포함돼 있으며, 여섯째 장 ‘균수’(均輸)에는 고대국가가 공평과세를 어떻게 실현하려고 했는지를 엿볼 수 있는 문제가 등장한다. 일곱째 장 ‘영부족’(盈不足)과 여덟째 장 ‘방정’(方程)은 모두 연립방정식에 관한 것이다. 그리고 마지막 장 ‘구고’(句股)는 산학에서는 ‘구고술’이라 부르는 피타고라스 정리를 활용한 문제로 이뤄져 있다.

이런 내용은 현재 중·고등학교 수학교육과정을 상당히 포함하고 있으며 어떤 문제와 풀이에 있어서는 현재와 다른 기발한 아이디어가 번득인다. 구장산술의 해법을 따라가다 보면 수학을 공부하는 새로운 기법을 터득할 수 있을 것이다.

또 구장산술은 산업, 행정, 교통, 토목·건축 등의 여러 분야에서 고대사회가 당면하고 있던 현실문제들을 반영했으며, 그 문제들에 대해 나름대로 수리적 해법을 제시했다. 물론 이렇게 현실과 깊이 관련있기 때문에 이 책은 단순한 수학교과서의 차원을 넘어서 동양 전통사회에 관한 훌륭한 정치·경제학서로 바라볼 수도 있다. 그러나 좀더 순수하게 수학적인 측면에서 바라볼 때, 구장산술의 최대 매력은 그것이 수학의 기원과 발생에 대해 우리에게 많은 시사점을 제공해준다는 점이다.

최초로 해의 고도 측량법 제시

여기서 구장산술에 나오는 문제 중 한가지 예를 살펴보자. 중차법이라 불리는 이 문제는 구장산술의 저자 유휘가 서문에서 소개한 것으로 해의 고도를 측량할 수 있는 방법을 설명하고 있다.

“무릇 지극히 높은 것을 바라보고 아주 깊은 것을 측량해서 그 거리를 알아내려면, 반드시 중차를 이용해야 한다. 직각삼각형은 반드시 중차를 비율로 삼아야만 하므로, 중차라고 하는 것이다. 낙양성에 막대 두개를 세워 높이는 8자가 되게 하고, 남북 양쪽 평지 끝에 두어 같은 날 해가 남중할 때(남쪽에 가장 높이 떠오를 때)의 그림자를 재도록 한다. 그림자의 차이를 나눗수, 막대높이와 막대간 거리의 곱을 나뉨수로 삼아서 나눴을 때 얻어진 값에 막대높이를 더하면, 곧 해에서 땅까지의 거리가 된다. 남쪽 막대 그림자와 막대간 거리의 곱을 나뉨수로 삼아서 나눠주면, 곧 남쪽 막대로부터 남쪽의 해 바로 아래에 있는 곳까지의 거리가 된다.”

중차술에 대한 유휘의 설명은 언뜻 봐서는 몹시 혼란스럽다. 그러나 이것을 그림을 그려 접근하면 좀더 쉽게 이해할 수 있다. 그림의 왼쪽위 꼭지점에 남중할 때의 해가 떠있다고 보자. 거기서 바로 밑에 있는 지점까지의 거리(해의 높이)를 x, 막대의 길이를 h, 태양에서 제일 가까운 지점으로부터 처음 막대를 세웠던 지점까지의 거리를 y, 그리고 그 자리에서의 그림자길이를 l1, 그 다음에 막대를 일직선상으로 이동시킨 거리, 즉 중차를 d, 그리고 새로운 지점에서의 그림자길이를 l2라고 하자.

그러면 아무래도 제일 먼저 눈에 들어오는 사실 가운데 하나는 두종류의 닮은 꼴 삼각형이다. 이들로부터

h : ${ι}_{1}$ = ( χ- h ) : y
h : ${ι}_{2}$ = ( χ - h ) : ( y + d )
라는 비례관계가 성립된다. 이 비례식들은

y = $\frac{(χ-h)ι₁}{h} $= $\frac{(χ-h)ι₂}{h} $ - d
라는 식으로 정돈될 수 있으며, 이 관계로부터

$\frac{(χ-h)(ι₁ι₂)}{h} $ = d

라는 식이 도출된다. 해에서 땅에 이르는 최단거리, 즉 해의 고도인 x가 바로 이식을 재정돈하면 얻어진다는 것은 더 말할 나위가 없다.

χ = $\frac{hd}{ι₁-ι₂} $+ h

그리고 이로부터 해 바로 아래 지점에서 처음 막대까지의 거리인 y도 구할 수 있다.

y = $\frac{ι₁d}{ι₂-ι₁} $

위 x와 y의 결과를 보고 음미하면 바로 “그림자의 차이를 나눗수, 막대높이와 막대간 거리의 곱을 나뉨수로 삼아서 나눴을 때 얻어진 값에 막대높이를 더하면, 곧 해에서 땅까지의 거리가 된다. 남쪽 막대그림자와 막대간 거리의 곱을 나뉨수로 삼아서 나눠주면, 곧 남쪽 막대로부터 남쪽의 해 바로 아래에 있는 곳까지의 거리가 된다”고 한 유휘의 말과 정확하게 일치함을 알 수 있다.

세계최초로 행렬식 개발한 일본인

개개인이 자라나면서 수학적 지식을 습득하는 과정은 상당한 정도까지 인류문명이 낳은 수학의 역사를 되풀이한다고 볼 수 있다. 따라서 구장산술 속에 고스란히 담겨져 있는 황홀한 내실인, 한 문명권이 장구한 세월에 걸쳐서 축적해놓은 수학체계를 음미해보는 일이 수학공부에 어찌 도움이 되지 않겠는가. 게다가 이것은 그동안 등한시돼 왔던 과학분야의 문화전통을 접하게 됨으로써 우리의 정체성 내지 역사의식을 새롭게 다질 수 있는 계기가 될 수도 있다.

그리고 사람에 따라서는 이로부터 창조를 위한 불씨를 발견할 수도 있다. 임진왜란 때 우리에게서 ‘조선간 동활자판’으로 된 산학서들을 구해간 일본이, 아이러니컬하게도 바로 이것을 시발점으로 그네들의 자랑거리인 일본식 산학 ‘화산’(和算)을 발달시키고, 이 과정에서 세키 다카카즈(關孝和, 1640?-1708)처럼 세계최초로 행렬식을 개발해내는 등의 성과를 올리기까지 했던 사실은 바로 이런 문화전통 속에 숨어있는 엄청난 잠재력의 일단을 우리에게 일깨워준다.

이런 추구를 위해 유휘는 오래 전에 우리들을 격려한 바 있다.
 

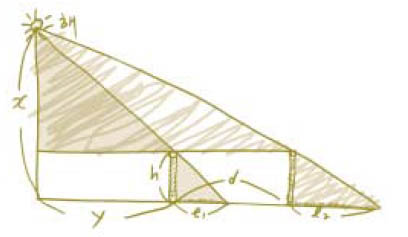
해의 고도를 측량하는 중차법

해의 고도(x)는 길이가 h인 막대기 두개 사이의 거리인 중차(d)를 이용해 구한다. 먼저 두종류의 닮은꼴 삼각형으로부터 h : l₁ = (x-h) : y, h : l₂ = (x-h) : (y+d)라는 비례식이 성립한다. 이 두식을 y에 대해 정리하면 해의 고도

x = $\frac{hd}{{l}_{2}-{l}_{1}}$ + h를 얻을 수 있다.