d라이브러리

여름날 하루살이가 떼지어 움직일 때 어느 한 마리만을 주목해 보면 제멋대로 움직이는 것처럼 보인다. 그러나 전체적인 한 덩어리로 보면 그 속에서 하나의 법칙에 따라 움직이고 있음을 알 수 있다. 이처럼 전체와 하나의 관계를 생각하는 것이 확률이며, 전체적인 흐름을 보는 것이 통계다.

인생은 우연의 연속이다. 하지만 인간은 우연에 압도당할 수만은 없었다. 그리하여 많은 지성인들이 우연에 도전하기 시작했다. 그 첫째 방법은 우연으로 보이는 것에 대해 법칙을 찾는 일이다.

링컨(Abraham Lincoln, 1809.2.12-1865.4.15)과 케네디(J.F.Kenndy, 1917-1963)는 둘 다 미국 대통령이면서 이상하게도 (표1)과 같은 유사점이 있다.

이와 같은 우연의 일치를 보면 그 이유를 묻고 싶다. 하지만 이것은 희귀한 일치이며, 그 속에서 법칙성을 찾기가 어렵다. 억지로 그 이유를 찾다보면 미신을 낳을 수 있다.
 

신학과 도박에서의 수학

파스칼(B. Pascal, 1623-1662)은 독실한 종교가였다. 그는 '인간은 항상 무엇인가를 결정하며 살아간다'고 하며 신을 믿는 일을 도박에 비유하고 있다.

"신이 있는지, 없는지는 알 수 없으므로 신을 믿는 일은 하나의 도박일 수 있다. 하지만 일단 신의 존재를 믿는다면 무한대의 행복을 기대할 수 있다. 곧 행복의 기대치는 무한대이며, 믿지 않았을때의 기대치는 무시할 정도로 적다. 그러기에 신을 믿어야 한다."

프랑스 도박의 귀족 마레경이 한때 도박에서 돈을 많이 잃어 '재수의 원리는 무엇인가' 하는 문제에 골몰했다.

"주사위를 던지면 반드시 1의 눈이 나오는가?"

그 답은 단 한번만 던지는 것이라면 반드시 나온다고는 할 수 없으나 던지는 횟수가 증가하면 그 던진 횟수의 $\frac{1}{6}$의 비율로 1의 눈이 나온다고 추측해도 좋다.

마레경이 이것을 근거로 해서 당시 제일의 수학자인 파스칼에게 "두 개의 주사위를 던져 둘 다 6의 눈이 나오도록 하기 위해서는 몇번 던지면 그 비율이 $\frac{1}{2}$을 넘는가?"라는 문제를 내놓았다. 마레경은 다음과 같이 풀었다.

"우선 하나의 주사위를 던지는 경우에 4번 던지면 6의 눈이 나올 확률은 $\frac{1}{2}$이상이 된다. 즉 그 비율은 4:6이 되므로 두 개의 주사위를 던지는 경우라면 같은 비율로 해서 24:36이 된다."

파스칼은 마레경의 풀이를 듣고 "마레경이 지혜는 있으나 수학적인 소질은 없다"고 말하고 다음과 같이 답을 제시했다.

"하나의 주사위를 던질 때 6의 눈이 나오지 않을 확률은 $\frac{5}{6}$이므로 4번 되풀이해서 6의 눈이 나오지 않을 확률은 ${(\frac{5}{6}})^{4}$이다. 그러므로 그 반대현상이 일어날 확률은 1－${(\frac{5}{6}})^{4}$이다."

이 파스칼의 주장은 옳다. 아무렇게나 주사위를 던져서 생기는 우연의 소치라고 할 수 밖에 없는 일에도 자세히 살펴보면 무엇인가 하나의 법칙이 지배하고 있다는 것이 확률론을 뒷받침하는 철학이다.

파스칼은 이 일을 계기로 해서 확률론의 기초를 확립했다. 도박에서 확률이 나온 것이다. 점성술에서 천문학, 연금술에서 화학이 나온 것과 마찬가지로 인간의 욕망이 엉뚱하게도 과학을 낳게 한 좋은 보기다.

통계와 확률 동전의 양면관계

확률이란 어떠한 상황이 몇번이라도 되풀이될 때, 그 중 하나의 일만을 보면 우연히 일어날 수 있는 것이지만 여러번의 시행을 전체적으로 보면 어떤 법칙성이 발생할수 있다는 믿음을 가질 때 생겼다. 여름날 하루살이가 떼지어 움직이고 있다. 이들 중 어느 한 마리만을 주목해 보면 자기 멋대로 움직이는 것처럼 보인다. 하지만 전체적인 한 덩어리를 보면 그 흐름속에 하나의 법칙이 있어 그 법칙에 따라 움직이고 있음을 알 수 있다.

이와 같이 전체와 하나의 관계를 생각하는 것이 확률이며, 전체적인 흐름을 보는 것이 통계다. 따라서 통계확률은 동전의 앞뒤와 같은 관계가 있다. 그러나 학문으로서의 확률론과 통계는 서로 다른 경로에서 발생했다.

확률론은 르네상스 이후 상업이 번성한 시기에 일확천금의 꿈이 왕성했던 이탈리아에서 생겼다. '쨍하고 해뜰 날'을 노래한 시절에 도박이 성행한것이다.

확률론의 계보는 다음과 같다.

이탈리아 카르다노(G. Cardano, 1501-76) → 이탈리아 갈릴레이(Galileo Galilei, 1564-1642) → 프랑스 페르마(P. Fermat, 1601-65) → 프랑스 파스칼(B. Pascal, 1623-1662) → 스위스 베르누이(J. Bernoulli, 1654-1705) → 스위스 베르누이(D. Bernoulli, 1700-1782) → 프랑스 뷔퐁(C.G.L.L. Buffon, 1707-88) → 프랑스 라플라스(P.S.Laplace, 1749-1827)

확률론 형성기의 처음 두 사람과 두 베르누이를 제외하면 모두 프랑스인이며, 특히 파스칼은 확률론의 창시자로 지목돼 있다. 당시 서서히 일어난 자본주의적인 사고와 난숙기에 있던 귀족사회의 돈 많은 프랑스 귀족들에게 도박이 유행한 것이다.

라플라스의 확률정리

확률은 라플라스(Laplace)에 의해서 정의됐다. 어떤 하나의 시행에서 생길 수 있는 모든 경우의 수가 N이면 이들 N개의 경우는 똑같은 정도의 가능성을 가지고 있다. 이 N개중 K개가 생기는 확률은
$\frac{K}{N}$ 이다.

트럼프에는 52장의 카드가 있다. 이 중에서 하나를 뽑을 때 생기는 모든 경우의 수는 52가지.그 중 하트(♡)일 경우 K＝13이므로 ♡가 나올 확률은
$\frac{13}{52}$＝$\frac{1}{4}$
이 정의를 이용해서 다음 문제를 생각해 보자.

흰색 빨강색의 두 가지 색으로 구분된 원판이 있다. 빨강색은 $\frac{1}{4}$, 흰색은 $\frac{3}{4}$을 차지한다. 이 원판을 돌리면서 화살을 던졌다. 빨강 부분에 맞힐 확률은 얼마인가?

이와 같은 경우 확률이 생길 수 있는 경우는 w x y z의 4가지. 이때 w x y z가 각각 생길 수 있는 가능성이 같다면 간단하다. 그것은 앞서 설명한 라플라스의 정의에 따라 $\frac{1}{4}$,씩이 된다. 하지만 w x y z가 나타나는 가능성이 같지 않을 때는 문제가 달라진다.

지금 w x y z가 생길 수 있는 가능성은
w:x:y:z
라고 한다. 이때 각각의 경우가 생길 수 있는 확률은 다음과 같다.

P(w)＝$\frac{w}{w+x+y+z}$
P(x)＝$\frac{x}{w+x+y+z}$
P(y)＝$\frac{y}{w+x+y+z}$
P(z)＝$\frac{z}{w+x+y+z}$

표적을 4등분하면 화살이 명중할 가능성은 표적이 중심에서 90°씩 분할돼 있으므로 똑같다. 그러나 빨강색 부분은 하나인 데 비해 상대적으로 흰색부분은 3개나 있다. 이를 식으로 표현하면 다음과 같다.

횐색부분에 명중할 확률은 $\frac{3}{1+3}$＝$\frac{3}{4}$
빨강부분에 명중할 확률은 $\frac{1}{1+3}$＝$\frac{1}{4}$

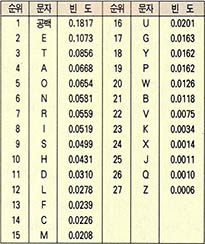
영어에는 26개의 알파벳이 있다. 어떤 한 문장에 무작정 바늘을 꽂았다. 이때 a에 맞힐 확률을 얼마일까? 알파벳은 26개이나 단어와 단어사이에는 공간이 있으므로 그것도 문자로 생각해 총 문자의 수는 27로 본다. 문자의 수가 27개라고 해서 그 중의 하나인 a에 맞힐 확률이 단순히 $\frac{1}{27}$이 아님을 금방 알 수 있다.

영어로 쓰여진 책을 조사하고, 평균적으로 각 문자가 쓰여지는 상대빈도를 만들어야 한다. (표3)은 수많은 책에서 검출한 영어문자의 빈도표다.

빈도＝ $\frac{문자가 사용된 횟수}{문자의 총수}$

가령 a의 빈도 0.0668은 임의의 영문에서 하나의 문자를 무작정 택했을 때 그것이 a의 문자가 될 확률을 나타낸 것이다.

확률의 최대값은 1, 최소값은 0

확률은 어떤 사건에 대한 전체 일어날 수 있는 경우와의 비이므로 확률값은 0과 1사이의 실수로 주어진다. 즉 A사건이 일어날 확률 P(A)는
0≤P(A)≤1이다.

또한 어떤 사건 A가 일어날 확률을 P(A)라 하면, 사건 A가 일어나지 않을 확률은
1－P(A)
로 구할 수 있으며, 이것을 사건 A에 대한 여사건이라 한다.

(1) ▶ 주사위를 던졌을때 1에서 6 눈가운데 어느 것이 나올 확률은 $\frac{6}{6}$이므로 1이다(주사위는 정육면체이며 어느 면도 평등적(같은 모양)으로 만들어져 있다).
▶ 주사위를 아무리 던져도 그것이 모, 또는 모서리로 설 수는 없다.
(2) ▶ 10원찌리 동전을 던졌을 때 앞 또는 뒷면이 나올 확률은 $\frac{2}{2}$이므로 1.
▶ 동전을 아무리 던져보아도 결코 옆으로 설수는없다.
(3) ▶ 차 안에 있는 1백명의 사람이 남자 또는 여자가 될 확률은 $\frac{100}{100}$이므로 1.
▶ 여자도 아니고 남자도 아닌 인간은 없다(상식적으로).
확률의 최대값은 '1'이며 최소값은 '0'이다. 따라서 아무리 확신해도 1백50%, 즉 1.5라는 확률은 없다.

확률과 미신

(1) 입시의 경우 합격 아니면 불합격이라고 해서 확률도 $\frac{1}{2}$일까? 아니다. 그것은 제비로 뽑아서 하는 것이 아니기 때문이다. 합격 여부는 학생의 실력에 달려 있으므로 합격, 불합격의 기회가 수치로 공평하게 주어져 있는 것은 아니다.

(2) 전쟁에서 살아남는 비결(미신)이 있다. 적의 포탄이 떨어져 파헤쳐진 구멍에 숨으면 다음 포탄이 맞지 않는다는 것이다. 그러나 처음 포탄이 떨어진 후 그 다음의 포탄은 처음 떨어진 포탄과는 전혀 관계가 없다. 그러므로 처음 포탄이 떨어진 것과 같은 확률로 그 다음의 포탄이 그 자리에 떨어진다.

(3) 아들, 딸이 출현하는 확률은 $\frac{1}{2}$이다. 또 그 다음에 태어나는 아이가 남자, 여자가 되는 확률도 $\frac{1}{2}$이다. 처음에 아들이 태어났다고 해서 다음에 태어나는 아이가 여자라는 법은 없다. 10형제중 모두가 남자인 경우, 또 그 반대로 여자아이만 10명 태어난 실례가 있다.

도박에 항상 이기는 방법은 있는가
 

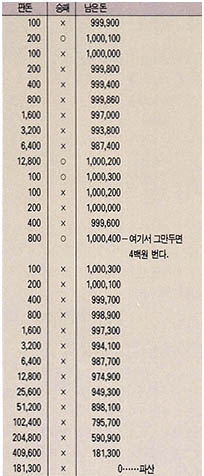
도박에 마음대로 이길 수 있는 것은 돌로 금을 만드는 것과 다름없는 인간의 욕망이다. 그러나 그 일이 가능하다는 이론이 있다. 즉 처음 1(백원짜리 동전 하나)을 건다(표4). 이기면 상대방이 건 것을 포함해 2를 얻는 것임으로 결국 1을 번 셈이다.

이긴 다음에는 또 하나를 걸고 게임을 계속한다. 그러나 질 때는 하나를 빼앗기는 것이므로 그 다음에는 2를 건다. 그래도 졌을 때는 판돈의 2배인 4를 건다. 그래서 또 한번 지면 2배인 8을 건다.

이와 같이 이길 때까지 계속 2배씩 걸면서 게임을 계속한다. 아무리 운이 나빠도 반드시 이길 때가 있다. 이와 같이 하면 결국 언젠가는 내가 이길 때 그 전까지 잃은 것을 모두 회수하고도 상대방이 건 1만큼 얻는다.

가령 7번까지 계속하고 8번째에 이겼을 때 7번째까지 잃은 돈의 총 합계는 1백27. 그러나 8번째는 이겨서 1백28을 얻었으므로 1을 번 것이 분명하다.

게임에 이기는 승률이 $\frac{1}{2}$보다 적다고 하더라도 계속 끈기있게 해 가면 언젠가는 이길 것이다. 그때마다 그 이전에 건 것을 완전히 회수하고도 1을 번다. 하지만 상당한 돈을 준비해야 하고 또 준비한 돈에 비해서 벌이는 적다. 해볼 만한 일일까? 실험을 한번 해보자.

주사위를 던져 1이 나오면 돌쇠가 이기고, 그 이외의 눈이 나오면 바위가 이기기로 한다. 승률이 적은쪽이 판돈을 마음대로 정한다는 조건이 있다. 즉 판돈은 모두 돌쇠가 정하기로 했다.

처음 판돈을 1백원으로 정하고 돌쇠는 준비금으로 판돈의 1만배인 1백만원을 준비했다. 그러나 실제로 게임을 진행했을 때 1백만 원을모두 잃었다. 그 결과는 (표5)와 같다.

(표5)에 의하면 준비한 돈이 많을 경우 오래 계속하지만 적당한 때에 끊고 4백원 정도 벌어서 만족하지 않는다면 결국 준비한 돈 모두를 잃도록 돼있다. 그 이유는 판돈이 그의 제곱으로 늘어가기 때문이다. 또 웬만큼 돈을 준비해도 금방 돈을 잃게 되기 때문이기도 하다.

이 사실을 기대치를 가지고 생각해 보자. 즉 승률은 $\frac{1}{6}$, 준비금은 8번까지 계속할 수 있도록 (${2}^{8}$－1)×100원을 준비했다고 가정하자. 8번 계속해서 지는 확률은
${(1-\frac{1}{6})} ^{8}$≒0.232
파산으로 인한 손해의 기대값은
0.232×25,500≒5,920
파산하기 전에 이길 확률은
1－0.232＝0.768
이겼을 때 1백원 벌고 처음으로 돌아가는 것이므로 벌이의 기대값은
0.768×100≒76.8≒80

손해의 기대값이 5,920 벌이의 기대값이 80이므로 손해가 큰 것임을 알 수 있다. 이 경우는 승률이 $\frac{1}{6}$밖에 안 되기 때문이라고 생각할 수도 있다.

그렇다면 승률이 $\frac{1}{2}$(50%)이라면 어떻게 될 것인가. 알아보기로 하자. 미리 준비한 돈은 앞의 경우와 같이 게임은 8회까지 할 수 있도록 25,500원으로 한다. 돈이 완전히 없어질 때, 즉 파산으로 인한 손해의 기대치는
${(\frac{1}{2}})^{8}$×25,500＝$\frac{25,500}{256}$
이고 이겼을때의 기대값은
{1－${(\frac{1}{2}})^{8}$}×100＝$\frac{25,500}{256}$
승률이 $\frac{1}{2}$이면 손해와 이익의 기대치가 일치해짐을 알 수 있다. 평균하면 득, 실이 없다는 결과다.

그러나 승률이 $\frac{1}{2}$보다 크면 이익을 보는 가능성이 많아지므로 유리하다. 그래도 현실적으로 승률이 $\frac{1}{2}$보다 큰 게임(경마, 도박)은 없다.

교훈같은 결론이지만 도박은 하지 않는 것이 좋다는 것이다.
 

통계의 역사

우리나라는 통일신라 전부터 정책에 숫자가 사용되기 시작했으나 서양에서는 로마시대 이후 적극적으로 통계적 방법을 사용했다. 영어로는 나라를 state라고 하는데 state에 또한 상태라는 의미도 있다. 그래서 통계학을 나라의 상태를 조사하는 것이라는 의미에서 statistic이라고 했다. 주로 정치 행정의 필요상 인구 종교 산업정책의 숫자적인 자료를 수집했다.

기원 전 2500년경 이집트에서 세계 최대의 피라미드를 건설했을 때 10만의 인원이 동원돼 20년 가까이 작업을 했다. 또 진시황이 만리장성을 쌓을 때도 석재 나무 노동자의 식량 등 엄청난 숫자를 다루어왔음이 분명하다. 하지만 이런 수들이 개개로 나열된 수표(數表)만으로는 통계학이 성립하지 못한다.

처음 통계학은 1662년 영국의 그란트(J. Graunt, 1620-1674)가 저술한 '사망표에 관한 자연적 및 정치적 문제'로 부터 시작됐다. 당시 영국은 해지는 날이 없는 대제국이었고, 런던에는 전세계의 문화가 들어오는 것과 함께 전염병의 병균도 들어왔다. 영국은 여러 차례 페스트의 전염에 시달렸다. 그 무렵 런던 시민의 $\frac{1}{2}$이 페스트를 피해 시외로 피난했을 정도였다.

이 무렵 시 당국에서는 '사망표'를 매주 목요일에 발행하기도 했었다. 시민은 이 표를 보고 사망자의 수를 화제로 삼았다. J. 그란트는 이 사망표를 보고 있는 사이에 '사망표 한 장 만은 그냥 숫자의 나열에 지나지 않지만 열 장의 표를 살펴보면 무엇인가 법칙성이 있다'는 것을 알아낸 것이다.

이런 사실을 정리해 발표한 것이 앞서 말한 책이다. 그것이 곧 통계학의 시작이다. 몇개의 자료만으로는 알 수 없는 사실을 많은 자료, 오랜 기간의 관찰에서 '법칙성' 또는 '경향'을 알아내는 것이다. 피라미드 만리장성의 건설책임자도 동원인부 석재 목재 등에 관한 수를 파악할수 있었다. 하지만 그것들은 한낱 자료에 불과하지 통계학이라고는 할 수 없다.

1623년 영국의 패디는 저서 '정치산술'을 발표했다. 여기에는 통계학을 기반으로 정책을 논한 내용이 담겨 있는데, 이것이 후에 스미스(A. Smith)의 국부론에 큰 영향을 준다.

이와 같이 통계학은 주로 영국학자들에 의해서 시작됐다. 영국인의 실용적 경험적인 국민성을 잘 나타내고 있다. 현재의 통계학과 확률론은 종이의 앞뒤와 같다. 하지만 그 출생의 역사가 확률론이 프랑스, 통계학은 영국으로 대조적이며 그것이 시작되는 계기도 다르다.

패디의 '정치산술'은 뉴턴의 '프린키피아'가 이론물리학의 원리로 지목되는 것과 마찬가지로 사회과학의 원류로 꼽힌다. 이것이 거의 똑같은 시절 같은 영국에서 나온 것은 우연이 아닌 것이다.

서서히 근대화가 진행되고 산업사회, 근대적 합리주의 정신이 싹트기 시작할 때의 시대 정신이 반영된 것이다.