d라이브러리

컴퓨터 2진법의 원리를 반영한 태극마크는 미국「북캘리포니아 철도회사」의 로고로도 사용되고 있다.​

풀어보고

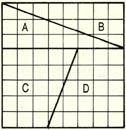
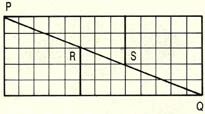
(1) 기하학에도 많은 파라독스들이 있다. (그림 A)에서는 8X8=64개의 정방형으로 구성된 정방형을 A, B, C, D의 4개로 나눴다. 이들을 (그림 B)처럼 다시 배열해 보니 13X5=65개의 정방형이 생겼다. 분명히 모순인데, 어느 부분에서 오류가 있었을까?
① A, B ② A, C ③ A, D ④ B, C
 

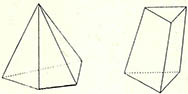
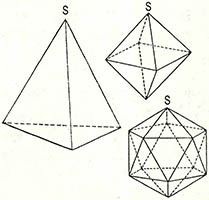
(2) 정다면체가 아닌 일반적인 다면체라고 하면 여러가지 형태가 가능하지만 사면체는 삼각형으로만 이뤄진다. 오면체가 되면 (그림)처럼 두 가지 형태를 나타낸다. 하나는 피라미드처럼 바닥은 사각형이고 각 변은 삼각형으로 구성된 오면체이고 다른 하나는 사면체에서 꼭지점 부근이 잘려진 형태의 오면체다. 전자는 삼각형 넷과 사각형 하나, 후자는 삼각형 둘과 사각형 셋이다. 그러면 육면체는 몇가지의 형태가 가능할까? 물론 주사위 같은 것도 그중하나다.
① 4 ② 7 ③ 9 ④ 11
 

(3) 우리가 쉽게 생각할 수있는 정다면체 (그 각 면이 모두 합동인 정다각형이고, 각 정점에서 생기는 정다각면이 모두 같은 입체)를 꼽으면 정사면체 정육면체 등이다. 계속 만들어 가면 정몇면체까지 만들 수 있을까?
① 정십면체 ② 정십이면체 ③ 정이십면체 ④ 정사십면체

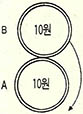
(4) 크기가 같은 두 개의 동전 A, B가 있다. 동전 A를 고정시키고 동전 B를 그 둘레를 따라 회전시킨다. 완전히 한바퀴 돌아 동전 B가 원래의 위치에 왔을 때 동전 B는 몇 번 회전했을까?
① 1 ② 2 ③ 3 ④ 4

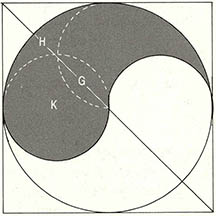
(5) (그림)과 같은 태극이 있다. 직선 하나를 그어서 두 부분을 각각 2등분하고 싶다. 어떻게 그리면 될까? 단, 이 태극은 큰 원 안에 지름이 반인 반원을 배치한 것이다.
 

맞춰보고

(1) ① 당연히 모순된 결과이므로 어디에선가 착오 난 부분이 있을 것이다. 문제는 (그림B)의 P와 Q를 연결하는 선이 C, B와 A, D를 연결할 때 완전히 아귀가 맞아 떨어지지 않는다는데 있다. 실제로는 이 선들이 벌어져 길다란 다이아몬드형의 공간을 갖게 되고, 이 공간이 바로 한개의 정방형의 크기와 같게 된다는 것이다.

직선 PR이 수평과 이루는 각도는 arctan (=${tan}^{-1}$)2/5, PS가 수평과 이루는 각도는 arctan 3/8이다. 따라서 그 사잇각은 arctan 2/5—arctan 3/8=arctan 1/46=1.245˚. 이 각도는 육안으로는 판별하기 어려운 작은 각이고, 이 때문에 착오가 일어난다.

arctan의 계산에 대해 알고 싶어하는 독자를 위해 설명하면 다음과 같다.
arctan 2/5-arctan 3/8=arctan c라 놓고 풀 때, arctan 2/5=α, arctan 3/8=β, arctan c=γ라 놓으면 tan α=2/5, tan β =3/8, tan γ=c가 된다. 위 식에 tan를 취하면, tan(α-β)=tan γ=c가 된다. tan의 각 뺄셈공식을 사용하면

tan(α-β) = $\frac{tan α - tan β}{1+tan α tan β}$= c
$\frac{\frac{2}{5} - \frac{3}{8}}{1+\frac{2}{5} - \frac{3}{8}}$ = $\frac{1}{46}$ = tan γ
따라서 γ=arctan 1/46이 된다.

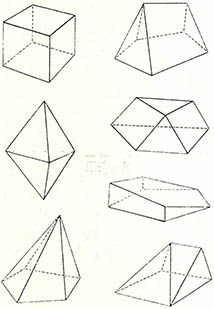
(2) ② 다면체란 평면다각형으로 이뤄진 입체다. 임의의 다각형으로 이뤄진 육면체는 모두 7가지다.
 

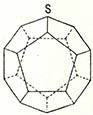
(3) ③ 정다면체는 정사면체 정육면체 정팔면체 정십이면체 정이십면체 등 다섯종류밖에 없다. 먼저 정육각형을 모아서 정다면체를 만들 수 있나 보자. 정육각형의 내각은 1백20˚인데, 정다면체의 한 정점 S에서 봤을 때 1백20˚X3˚=3백60˚이므로 정육각형 세개로 정삼각면각을 만들 수 없다. 즉 서로 아귀가 맞아 입체가 아닌 평면이 돼 버린다. 정다면체를 만들려면 한 정점에서 정다면각을 만들 수 있어야 하는데 그러기 위해서는 내각의 합에 다면의 수를 곱한 일이 3백60˚보다 작아야 한다. 이런 조건을 만족 시키는 것이 정육각형 이상에서는 불가능하다. 정오각형에 대해서 알아보자. 정오각형의 내각은 1백8˚이고 1백8˚X3=324˚＜3백60˚이므로 정오각형을 만들 수 있고, 이것이 정십이면체다.
 

정오각형을 4개 이상 모을 수는 없다. 그러나 정사각형 3개를 모아 정삼각면각을 만들 수 있다. 즉 90˚X3˚=2백70˚＜3백60˚이다. 이 경우는 정육면체가 된다. 4개를 모으면 정육각형 3개 모은 것처럼 평면이 돼 버린다. 정삼각형으로는 세가지 정다면체를 만들 수 있다. 정삼각형의 내각은 60˚이므로 60˚X3˚=1백80˚＜3백60˚, 60˚X4˚=2백40˚＜3백60˚, 60˚X5˚=1백80˚＜3백60˚의 세 경우가 각각 정사면체 정팔면체 정이십면체를 나타내게 된다. 정삼각형을 6개이상 모으는 것은 불가능하다.

그러므로 정다면체는 정삼각형으로 이뤄진 정사면체 정팔면체 정이십면체가 있고, 정사각형으로 이뤄진 정육면체, 정오각형으로 이뤄진 정십이면체 등 다섯가지가 있다.
 

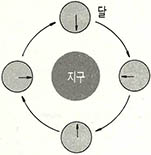
(4) ② 고정된 동전에서 보면 한번 회전한 것이지만, 우리가 보면 두 바퀴를 돈 것이 된다. 실제로 회전시켜 보면 90˚ 회전시켰을 때 이미 거꾸로 돌아 있고 1백80˚ 회전시키면 벌써 1회전을 하고 있다. 달이 지구를 한 바퀴 돌았을 때 달은 몇 회전을 했을까? 달의 표면은 지구 쪽으로 한 면 밖에 보이지 않으므로 0회전 했을까? (그림)에서 보면 달은 1회전한 것이다.

즉 같은 면만 보이도록 회전하면 1회전이고, 문제에서처럼 접촉하면서 돌면 2회전이 된다. 이 결과는 파라독스처럼 보이나 중요한 사실이어서 회전기계의 설계시 주의를 요하는 부분이기도 하다.
 

(5) 태극은 음양(영어로는 Yin, Yang)으로 구성돼 있다. 그 형태는 '북캘리포니아 철도회사'의 로고이기도 한데, 이 회사의 설계담당 중역이 1893년에 열린 시카고 세계박람회에서 우리나라 국기에 태극마크가 쓰여진 것을 보고 사용하기 시작했다. 그는 이 형태가 증기기관을 움직이는 불과 물을 잘 표현하는 것이라고 생각했다.