d라이브러리

닮은 점도 상반되는 점도 많은 우주의 세 괴천체는 서서히 그 정체를 드러내고 있다.

우주의 세 구멍-검은 구멍(black hole) 흰 구멍(white hole) 벌레구멍(worm hole)-은 서로 유사한 성질과 상반되는 성질을 가졌다. 그러므로 이러한 분류는 구멍이란 공통된 이름에서 비롯된 잠정적인 것으로 생각해야 한다. 검은 구멍을 제외한 나머지 두 개는 극히 불안정하여 순식간에 소멸한다는 공통성이 알려졌다.

또 세 구멍은 모두 우리의 상식에서 벗어난 이상한 천체(시공간)라는 점도 공통된다. 아무튼 셋 모두가 극히 강력한 중력때문에 빚어지는 현상이다. 우리의 상식에 어긋나는 까닭은 중력의 크기가 우리에게 친숙한 지구나 태양의 중력에 비해 엄청나게 큰 데 연유한다. 이러한 극한상황에서는 종래의 뉴턴의 중력이론이 무기력해지고 아인슈타인의 새로운 중력이론(일반상대성이론)이 요구된다.

일방적으로 삼켜버린다.

1960년대만 해도 천문학자들은 블랙홀(black hole) 즉 검은 구멍이란 천체를 반신반의(半信半疑)로 받아들이기가 예사였다. 그러나 그후 관측된 증거-X선을 내는 연성, 은하중심부의 활동영역 등-로부터 이제 검은 구멍은 다른 별이나 은하처럼 천문학의 실재대상으로 자리를 굳히게 되었다.

우리 태양계가 소속돼 있는 우리 은하(은하수)의 중심부에도 태양보다 1백만배나 무거운 거대한 검은 구멍이 있고 이 검은 구멍이 주변의 별들에 지대한 영향을 끼치고 있다는 게 거의 확실해졌다. 이러한 사실은 우리 이웃의 은하를 비롯해 이른바 활동성 중심부(active galactic nuclei)를 가진 은하들에 대해서 널리 추정되고 있다.

검은 구멍이 참으로 놀라운 것은 막대한 중력을 가지고 그 주변의 모든 물체를 '일방적'으로 삼켜버리는데 있다. 여기서 '일방적'이라는 뜻은 일단 검은 구멍 속으로 들어간 물체는 다시 검은 구멍의 중력으로부터 빠져나올 수 없다는 것이다.

보통의 어떤 천체에서 그 중력을 벗어나 외계로 물체가 탈출하는데 필요한 최소의 속도 V(이탈속도)는 그 이탈지점의 거리(천체의 중심부터)R과 천체의 질량 M에 의해 결정된다. 간단히 말해 M이 클수록 또 R이 작을수록 V는 커진다. 즉 중력이 클수록 이탈속도는 커진다.

지구표면(R이 약 6천4백㎞)으로부터 외계로 탈출하려면 이탈속도 V는 약 11㎞/초, 태양표면으로부터는 6백㎞/초 정도 돼야 한다. 질량이 M인 천체의 경우 이탈속도는 천체가 작아질수록 그 반경 R에 반비례해서 커지므로 어느 한계에 이르면 V가 광속도 C를 넘게 될 것이다. 그런데 물체의 속도는 광속도를 넘을 수 없으므로 결국 탈출이 불가능하게 된다.

이때 ${R}_{c}$(=2GM/${C}^{2}$, G는 중력상수)값을 '중력반경' 또는 쉬바르츠실트(Schwarzschild)반경이라고 한다. 즉 천체의 반경이 ${R}_{c}$이하로 작아지면 모든 물체나 빛은 그 표면으로부터 탈출할 수 없으므로 반경이 ${R}_{c}$인 면을 검은 구멍의 표면으로 생각할 수 있다. 다시 말해 검은 구멍이란 빛이 나올 수 없고, 모든 물체(빛도 포함)를 일방적으로 삼켜버리는 구멍을 말한다.

검은 구멍처럼 '검은' 물체는 어디에도 존재하지 않을 것이다. 왜냐하면 보통의 검은 물체는 모든 색(파장)의 빛을 잘 흡수하지만 일방적으로 흡수만 하는 것이 아니기 때문이다. 예컨대 검은 숯도 상온(常溫)에서 눈에 보이지 않는 적외선(붉은 색의파장보다도 긴 파장을 가진 복사)을 내고 있고 고온에서는 붉은 빛을 내고 있음을 우리는 잘 알고 있다.

중력반경 ${R}_{c}$는 지구의 경우 불과 약 1㎝, 태양의 경우 3㎞ 정도이므로 지구와 태양을 검은 구멍으로 만들려면 각각 6천4백㎞를 1㎝로, 70만㎞를 3㎞로 줄이는 터무니 없는 압축이 필요하게 된다.
 

별의 진화과정을 통해

그렇다면 검은 구멍은 애당초 어떻게 해서 태어났을까. 오늘날 널리 인정되고 있는 별의 진화이론에 따르면 별의 진화(일생)에서 마지막 단계에 이르면 별이 지구 정도의 크기로 축소된다고 한다. 현재 태양은 70만㎞나 되는 크기를 일정하게 유지하고 있다. 태양이 자신의 무게로 인해 으스러지지 않고 제 모습을 지탱하는 까닭은 고온의 내부에서 떠받고 있는 압력이 태양의 무게(약 2x${10}^{26} $t, 1조(兆)t의 2백조배, 지구의 33만배)를 감당하고 있기 때문이다. 태양 중심부의 압력은 약 27억기압으로 추정된다. 이러한 엄청난 압력은 태양 중심부에서 일어나고 있는 원자핵 반응(4H→He), 즉 수소폭탄의 폭발에 해당하는 반응때문에 고온고압이 유지되고 있는 것이다. 이러한 원자핵반응으로 별의 내부에는 차츰 더 무거운 원소가 합성돼 -수소(H)→헬륨(He)→탄소(C)→질소(N)→산소(O) 등- 별의 내부상태나 크기 밝기 표면온도 등이 서서히 변하는 별의 진화가 진행된다. 이러한 변화는 수백만년 내지 수십억년의 오랜 세월에 걸쳐서 일어나므로 진화라고 말하지만 시간이 길다 뿐이지 별의 일생이라고 생각할 수 있다.

별의 일생이 끝날 무렵에는 내부에서 일어나야할 원자핵반응이 땔감의 고갈로 인해 더 이상 이뤄질 수 없게 된다. 따라서 압력이 줄어들고 자체의 무게를 지탱할 수 없게 되므로 수축할 수밖에 없다.

별의 일생의 마지막 단계는 별의 질량에 따라 세 경우로 구분된다. 태양의 질량 ${M}_{s}$를 기준으로 해 M<;1.4${M}_{s}$인 별은 고온(백색)의 작은(태양의 약 1백분의 1 크기) 별('백색왜성'이라고 한다)로 축소돼 차츰 냉각되면서 우리의 시야로부터 사라진다.

그러나 3${M}_{s}$>;M>;1.4${M}_{s}$인 별은 더욱 축소돼 크기가 10㎞ 정도의 중성자별로 변한다. 이러한 별이 생기기 전에 M.${M}_{s}$인 별의 큰 폭발이 일어나는데 이때 별의 밝기는 1억배 가까운 밝기로 증가한다. 이 광경은 마치 새로운 별이 태어난 것처럼 보이므로 초신성(超新星)으로 불린다.

1987년 2월 남반구 밤하늘에 나타났던 초신성은 15만광년 떨어진 큰 마젤란운(Large Magellanic Cloud)속의 별이 폭발한 것이었는데 맨눈으로 볼 수 있을 정도로 밝았다. 후에 그 자리에는 중성자별이 남겨진 것으로 추정되고 있다.

중성자별은 중력수축으로 수소원자핵과 전자가 붙어서 중성자로 변한 거대한 원자핵과 같은 작은 별이다.

M>;3${M}_{s}$인 별은 내부의 압력때문에 무게를 지탱할 수 없게 되므로 검은 구멍으로 수축한다.

검은 구멍의 표면(반경 ${R}_{c}$인 구면)을 '사건의 지평선'이라고도 하는 까닭은 그안으로부터는 아무런 정보(물질 빛 등)가 나오지 않기 때문이다.

성간여행의 지름길-웜홀

웜홀(worm hole), 즉 벌레구멍은 검은 구멍의 사촌뻘이 되는 시공간이라 할 수 있다. 즉 우주(시공간)의 구조를 결정하는 중력의 방정식에서 검은 구멍과 비슷한 성질을 가진 해(解)를 통해 얻어진다.

그런데 이 벌레구멍은 시공간 사이를 잇는 좁은 지름길의 역할을 할 수 있다는 점에서 학자들의 관심을 끌게 되었다. 실제로 사람들은 검은 구멍보다도 먼저 벌레구멍을 성간여행(星間旅行)의 지름길로 이용하고자 했다.

아인슈타인이 일반상대성이론을 발표한지 1년도 채 안되어서 오스트리아의 물리학자 플람(Flamm)은 구대칭(球對稱, 한 점으로부터의 거리에만 의존하고 방향에는 무관하게 한) 중력장에 해당하는 중력방정식의 해(解) 가운데 벌레구멍은 1920년대에 수학자 와일(Weyl), 30년대에는 아인슈타인과 로젠(Rosen), 50년대에는 미국이 물리학자 휠러(Wheeler) 등에 의해 연구됐다.

사과의 표면에서만 움직일 수 있는 2차원 공간의 벌레는 표면의 두 점 사이를 표면을 따라서 갈 수 밖에 없다. 그러나 제3의 차원이 허용된다면 두 점을 직선으로 잇는 -사과속으로 파들어가는 벌레구멍-지름길이 있다. 이와 마찬가지로 별과 별 사이, 또는 우리 은하와 다른 은하 사이에서도 이러한 지름길을 생각할 수 있다.

모든 지름길이 그렇듯이 지름길이 갈라지는 곳에서는 길이 급하게 꺾어지는 법이다. 즉 벌레구멍은 시공간이 급하게 구부러지는 곳에서 시작된다. 아인슈타인에 따르면 시공간의 구부러짐이 중력과 동등하므로 여기서는 강한 중력이 작용할 것으로 짐작된다. 검은 구멍과 벌레구멍이 서로 관련을 가지게 되는 까닭이 여기에 있다.

중력이 시공간을 구부러뜨리는 것을 설명하기 위해서 평탄한(중력이 없는) 시공간을 고무로 된 평면으로 나타내고 여기에 물체를 올려놓았을 때를 상상해 보자.

틀림없이 고무평면은 물체의 중력으로 인해 아래로 처지게 된다. 여기서 고무평면이 처지는 실제 이유는 물체의 무게(지구의 중력)에 있지만 이것은 비유의 편이상 부득이한 일이다.

물체의 질량이 클수록 고무평면은 크게 처지고 좁은 병목과 같은 모양으로 변한다. 마침내 이 병목은 끊기고 만다.

또 하나의 고무평면이 아래에 있다면 병목이 두 평면을 잇게 되는 상황도 가능하다. 이 두 평면(물체가 놓인 근방만을 보면 곡면도 평면과 별로 다를 바 없다)을 사과표면(곡면)의 벌레구멍으로 이어지는 두 곳으로 생각할 수 있다. 즉 벌레구멍은 두 시공간이나 동일 시공간의 두 곳을 잇는 시공간의 좁은 통로와 같다.

성간여행 또는 은하간 여행에 이용할 경우, 벌레구멍이 검은 구멍에서 출발했다면 검은 구멍의 일방통행성 때문에 그 종점에서는 반대의 일방통행성을 가진 구멍이 필요하다(일반 버스를 타본 사람이라면 누구나 이해가 갈 것이다).
 

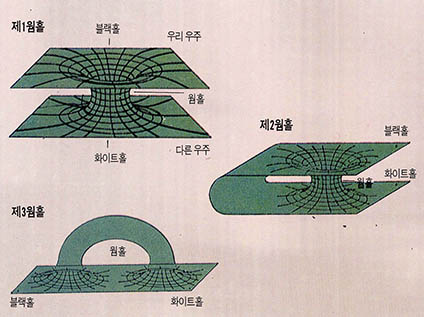
검은 구멍을 뒤집으면-화이트 홀

이 구멍은 검은 구멍과 반대되는 흰 구멍(white hole) 또는 역지평면(antihorizon)이라고 한다.

화이트 홀(white hole) 즉 흰 구멍은 수학적으로는 검은 구멍을 시간적으로 뒤집은 것이다. 아인슈타인의 중력방정식은 뉴턴의 중력방정식이나 양자론의 방정식과 같이 시간을 뒤집어도 그대로 성립한다. 그러나 흰 구멍이란 검은 구멍과 반대로 물체를 일방적으로 뱉어내는 구멍이므로 우리 상식으로는 검은 구멍 이상으로 이해하기 어려운 괴상한 개념이다.

그러나 전문가의 계산에 따르면 흰 구멍 근방으로 끌려오는(중력은 언제나 인력이다) 물체(빛)의 에너지가 급속히 증가, 흰 구멍을 순식간에 검은 구멍으로 탈바꿈시키고 만다. 태양 정도의 질량을 가진 흰구멍인 경우 그 수명은 약 1만분의 1초(?)에 지나지 않는다.

그 뿐만 아니라 벌레구멍 자체도 엄청난 장력(서로 당기는 탄력)이 걸린 고무줄처럼 순식간에 끊기고 만다.

그러므로 벌레구멍을 이용한 고속 성간여행은 사실상 불가능하다는 결론을 얻게되었다. 계산에 따르면 중성자별이 들어갈만한 병목의 경우, 여기에 걸리는 장력은 가장 무거운 중성자별의 중심압력(태양의 경우의 ${10}^{16}$배)에 해당하므로 벌레구멍의 소재가 될만한 강한 건축재는 결코 존재할 수 없다는 매우 실망스러운 결과가 얻어졌다.
 

우주는 죽음으로 향하고…

검은 구멍은 우주의 역사와 관련을 가지고 있다. 1854년 독일의 물리학자 폰 헬름홀츠(von Helmholtz)는 '우주는 죽음으로 향하고 있다'고 했다. 그는 자연현상이 일어나는 방향을 거꾸로 할 수 없다는 사실, 즉 비가역성(非可逆性)을 이렇게 표현한 셈이다. 예컨대 고무풍선에서 공기가 새나가는 현상, 뜨거운 물체를 내버려 두면 열이 주위로 발산해 곧 냉각되는 현상등을 필름으로 찍은 뒤 거꾸로 돌린다면 우리는 곧 이 영화가 뭔가 잘못되었음을 알아차릴 수 있다.

이러한 비가역성을 19세기의 과학자들은 "고립된 계(係, 입자들의 집단)의 엔트로피(entropy)는 시간이 지나면서 감소하는 일이 없다"고 표현했다. 이것을 열역학 제2법칙이라고 하는데, 이를테면 모든 상황은 내버려 두면 어지럽혀지게 마련이라는 얘기.

'엔트로피'란 그 집단의 무질서 정도를 나타내는 양인데 일반적으로 집단의 입자수가 많을수록 커지는 양이다.

보통의 물체는 수많은 입자(분자 원자)들의 집단으로 생각되는데 이런 집단에서는 입자의 확산(고무풍선의 공기가 빠지는 현상)이나 열의 이동(입자 사이의 에너지교환) 등이 일어나게 마련이다. 이처럼 자연현상의 비가역성은 쉽게 입증할 수 있다.

가령 집단내의 온도나 압력이 고르지 않은 상태라 할지라도 충분히 시간이 지나면 온도나 압력이 고른 열평형 상태로 변하게 된다. 이 상태는 확산이나 열이동 등 비가역현상을 거쳐서 이뤄지는 것이다. 물론 이 상태는 처음 상태보다도 엔트로피(무질서도)가 증가된 상태라고 볼 수 있다. 왜냐하면 처음 상태는 에너지가 밀도가 큰 입자들과 낮은 입자들이 구분된 상태라고 볼 수 있고, 나중상태는 그 구분이 없어져 완전히 뒤섞인 상태로 볼 수 있기 때문이다.

예로 어떤 분류에 따라 책장에 정리돼 꽂혀 있던 수많은 책들이 일반인에게 방치된 경우를 가정해 보자 시간이 많이 지난뒤에 살펴본 책들의 소재는 극히 무질서한(어느 책이 어디에 꽂힐지 예측할 수 없는) 상태로 변하기 십상이다. 즉 정리된 상태라 할지라도 시간이 흐르면 그 질서가 흐트러지게 마련이다.

보통 실험실이나 우리 생활주변의 규모가 작은 현상에서는 위에서 본 것처럼 비균질 상태에서 균질상태로 진행된다. 그래서 19세기의 과학자들은 우주가 오랜 세월이 지나면 엔트로피가 최대인 균질한 상태로 변해 모든 변화가 종식되는 죽음에 이를 것으로 예상했다.

그러나 이런 생각에 중력이 전혀 고려되지 않았다는 사실이 알려지게 되었다. 중력은 물체를 서로 이끌어서 뭉치게 하는 경향이 있다. 따라서 균질한 성간물질에서 별을 뭉치게 한다. 또 별들은 은하로 은하는 은하단으로 뭉쳐진다. 이처럼 시간이 흐르면 비균질상태로 변해가는 또다른 경향이 있다. 중력이 무시된 경우와는 반대방향으로, 즉 균질상태에서 비균질상태로 진행하게 되는 셈이다.

검은 구멍은 「대머리」

이러한 모순은 중력의 엔트로피를 고려하면 곧 해명된다. 예를 들어 균질한 기체가 뭉쳐져서 별이 생길 때 별의 엔트로피는 감소하지만, 수축으로 인해 뜨거워진 별이 주위에 방출하는 열을 고려하면 감소한 엔트로피를 웃도는 엔트로피의 증가를 얻을 수 있다.

우주의 팽창은 별이나 은하 같은 비균질한 덩어리를 만들어낸다. 아울러 이 덩어리가 내는 열이 저온이 된 주위(팽창에 따른 냉각으로 인해)로 흐르게 된다. 다시 말해 엔트로피의 증가를 계속 일으키는 것이다. 그러므로 우주의 역사는 엔트로피가 보다 높은 상태로 진행되고 있는 셈이다.

그러면 오늘날의 우주는 엔트로피가 얼마나 높은(또는 낮은) 상태에 있는 것일까. 여기서 우리는 검은 구멍의 엔트로피가 엄청나게 크다는 사실을 알 필요가 있다.

현재의 정보이론에 따르면 정보량은 수학적으로 음(-)의 엔트로피로 측정된다고 한다. 우리는 이 사실에 유의할 필요가 있다. 어떤 집단에 대한 정보는 그 집단의 질서(무질서의 반대되는 개념)와 관련됨을 금세 이해할 수 있기 때문이다.

그런데 검은 구멍은 그 사건의 지평선 밑에 있는 정보(빛 물질)를 차단하고 있으므로 무지(無知), 즉 엔트로피의 창고라고 할 수 있다.

검은 구멍이란 이름을 만든 휠러는 '검은 구멍'은 대머리(no hair)란 주장을 했다. 그는 검은 구멍으로부터 얻어 낼 수 있는 정보(털)는 총질량 총각(角)운동량 총전하(電荷) 등 세개에 한정되고 다른 지식은 결코 얻을 수 없는 검은 구멍의 정보결핍현상을 대머리에 빗대어 표현했다.
어떤 집단의 엔트로피는 그 집단속에 들어있는 입자의 총수(總數)로 가늠할 수 있다. 태양과 같은 별의 경우 총질량(약${10}^{33}$g)을 입자(수소원자 약 ${10}^{-24}$g)로 나눈 값, 즉 ${10}^{57}$ 정도로 가늠된다.

만약 태양이 검은 구멍이 되었다면 그 속으로는 모든 물체가 삼켜 들어가기 때문에 무한히 큰 엔트로피가 예상될지도 모른다. 그러나 실제로는 검은 구멍의 크기 ${R}_{c}$ 보다 입자의 크기 ${ℓ}_{c}$가 작아야 한다는 제한때문에 최대한의 입자수, 즉 엔트로피의 상한(上限)이 계산되는데 그 값은 M=${M}_{s}$일 경우 ${10}^{77}$나 된다. 즉 별인 경우에 비해 ${10}^{20}$배(1조x1억배)나 크다.

검은 구멍이 실재한다는 증거는 허다하게 드러났지만 아직도 별의 숫자에 비하면 그 수효는 무시할 정도로 적다. 그러므로 우주의 현재 엔트로피 보유량은 모든 별이 검은 구멍으로 탈바꿈할 먼 미래와 비교할 때 아직도 미미한 것으로 생각된다.