블랙홀(검은구멍)은 이론의 산물일까, 아니면 실제로 존재하는 것일까? 거대별이 수축하여 물질이나 빛이 빠져나올수 없는 거대한 중력의 수렁, 블랙홀의 신비를 벗긴다.
우주공간에 존재하는 블랙홀은 빛이나 물질 어느 것도 빠져나오지 못하는 검은 구멍을 말한다. 태양보다 무거운 천체가 강한 중력을 받아 수축되어 어느 한계에 오면 중력이 무한대가 되어, 그 곳에서는 빛 에너지 물질 입자의 어느 것도 빠져나오지 못한다.
검은 구멍(블랙홀)은 아인슈타인의 일반상대성 이론에 근거를 둔 것으로 오랫동안 이론상으로만 존재해왔으나 최근 인공위성에 실어보낸 X선 망원경으로 백조자리에 있는 X-1이라는 X선원(線原)을 발견, 이것이 검은 구멍일 가능성이 확실해 그 실제 가능성이 분명해졌다.
전형적인 검은 구멍이라 할 수 있는 태양의 20배의 질량을 가진 별도 반지름이 10여km로 축소되며 중력은 지구중력의 1백억 배로 엄청나게 크다. 검은 구멍의 수는 우리 은하계 안에 1억개 정도가 있는 것으로 추정된다.
시간과 공간이 역전하는 물리학의 새로운 영역을 차근차근 이론적으로 접근해보자.
이론이 파탄하는 물리학의 종점
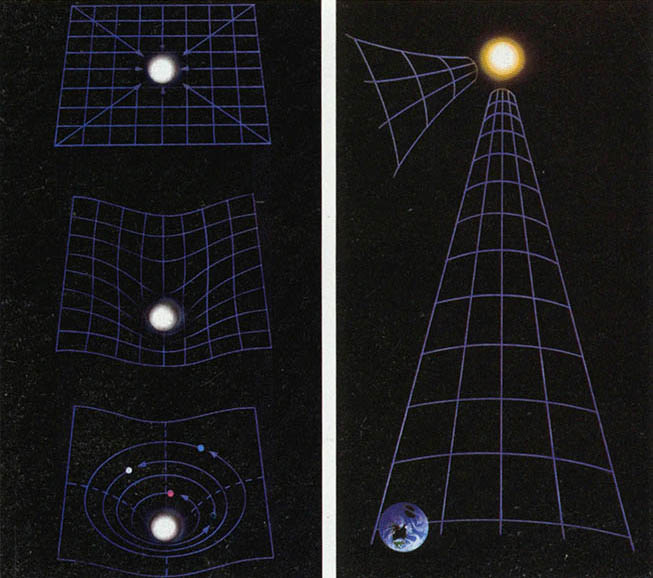
지구의 중력을 벗어나서 외계로 우주선을 보내기 위해서는 최소한 약11km/sec의 속도가 필요하다는 것은 잘 알려진 사실이다. 이 속도를 지구로부터의 이탈속도라고 한다. 이탈속도(v)는 천체의 질량(M) 반경(R) 중력상수(G=7×${10}^{-8}$C.G.S.)를 써서 v²=2GM/R로 주어진다. 위의 값은 M, R에 지구의 값을 써서 얻은 것이다.
물체가 가질 수 있는 속도의 한계는 빛의 속도(C=3×${10}^{10}$㎝/sec)이므로 위식에 v대신 C를 넣고 계산한 R의 값(R=2GM/C²)은 빛이나 물체가 이 천체의 중력에서 탈출할 수 있는 한계를 준다. 이것은 그 천체의 중력반경(${R}_{G}$)이라하여 태양의 경우 3km, 지구의 경우 약 1cm가 된다.
이 간단한 계산에서 알 수 있는 사실은 별의 크기가 ${R}_{G}$이하로 작아지면 빛도 빠져나올 수 없으므로 우리는 그 별을 볼 수없다는 것이다. 이런 사실은 이미 1795년에 수학자 '라플라스'(Laplace)가 '뉴튼'(Newton)의 중력이론을 써서 알아냈지만, ${R}_{G}$는 1917년에 '슈바르쯔실트(Schwarzschild)'가 아인슈타인(Einstein)의 중력이론 (일반 상대론)을 써서 얻어낸 한계값과 일치하므로 슈바르쯔실트 반경으로도 불리고 있다.
그는 공으로된 질량M의 둘레에 생기는 중력장(중력이 작용하는 공간)에서 공의 중심에서 ${R}_{G}$인 거리의 안팎에서 시간과 공간의 역할이 서로 뒤바뀌는 이상한 일이 일어나는 사실을 밝혔다.
즉 시간 t와 공간 R을 서로 수직인 두 축으로 잡을 때 R<${R}_{G}$에서는 R축이 t축으로 바뀐다는 것이다. 상대론에서는 1차원의 시간을 합한 4차원의 시공간(時空間)을 생각하는데, 이를테면 물체의 운동을 4차원 시공간의 곡선, 세계선(世界線)으로 나타내고, 일반적으로 물리학을 4차원 시공간의 기하학으로 변환한다.
그런데 공간과 시간과는 근본적으로 다른 점이 있다. 그것은 공간의 방향에서는 상하좌우로 각 공간축의 두 방향을 자유로 택할 수 있으나, 시간의 방향에는 한 방향, 즉 과거에서 현재를 거쳐 미래로 밖에 택할 수 없다는 것이다.
그러므로 R<${R}_{G}$에서 R축이 t축으로 바뀌면 R은 한 방향(이 경우 중심을 향하는)으로 변할 수 밖에 없다. 즉 R=O을 향하는 운명을 피할 길이 없다. 이것은 마치 우리가 늙어가는 운명(시간의 화살)을 돌이킬 수 없는 것과 다름없다.
R=O은 뉴튼역학으로 중력이 ∞(상대론으로는 시공간의 곡률이 ∞)되는 특이점(特異点)이다. 특이점은 이론의 파탄을 일으키는 영역, 즉 물리학의 종점을 가리킨다. 1960년대에 이르러 '휠러(Wheeler)는 ${R}_{G}$이하로 수축되어 빛이 나오지 못하는 천체를 '검은 구멍'(Black hole)으로 이름지었다. 검은 구멍 속의 특이점으로 치닫고야마는 천체의 중력붕괴(重力崩壞)는 물리학에 대한 만만치 않은 도전으로 받아들여지게 되었다.
그런데 보통 크기가 수십만- 수천만㎞에 달하는 별들이 이처럼 작게 수축될수 있을까?
거대질량 별의 마지막 모습
이미 1930년대에 크기가 태양의 1백분의1 정도의 고온의 별(백색외성)이 존재함이 밝혀졌다. 이런 압축된 상태에서는 전자들이 너무 압축된 결과, 같은 상태를 두 전자가 차지할 수 없는 배타원리(排他原理)에 따르는 양자역학적인 압력이 보통의 기체압력( ∝온도, 밀도)을 대신하여 별의 중력을 지탱하는 사실이 알려졌다.
그러나 별의 질량이 태양의 약 1.4배의 한계를 넘어서면 전자의 압력이 아니라 중성자의 압력으로 지탱하게 된다. 이 경우의 밀도는 백색왜성의 1억배가 넘는 원자핵의 밀도(${10}^{14}$g/ ㎤)에 달하고 그 크기는 10km 정도로 압축된다. 1938년에 '오펜하이머'(Oppenheimer) 등에 의해서 이러한 중성자별의 존재가 예견되었다.
1967년에 이르러 처음으로 전파의 펄스를 내는 '펄사'(pulsar)라는 별이 관측되었는데, 전파의 펄스와 빛의 변동이 매우 규칙적인 것으로 미루어 이는 반경이 10km정도의 중성자별이 빠르게 자전하는 것으로 설명되었다. 특히 2개의 펄사는 옛날의 초신성(超新星)이 폭발한 곳에 발견되었으므로 중성자별은 초신성 폭발의 유물로 추정되게 되었다.
그런데 중성자별도 질량이 어느 한계(태양의 3배정도)를 넘으면, 지나친 별의 무게를 지탱할 압력이 없으므로 별은 스스로의 무게 때문에 검은 구멍으로 수축을 할 수 밖에 없게 된다.
결국 별의 일생의 마지막 단계는 그 질량에 따라서 3가지로 나뉘어져서 백색외성(M<;1.4태양) 중성자별(M$\lesssim$3.0태양) 검은 구멍(M>;3.0태양)으로 된다.
일방통행의 반투막
중력반경 ${R}_{G}$의 구면은 외부로 나가는 빛(정보)이나 물체를 일체 차단해버리는 한계면으로 '사상(事象)의 지평선'으로 불린다. 이를 검은 구멍의 표면이라고 생각 할 수 있다. 검은 구멍은 막대한 중력의 수렁이므로 사상의 지평선은 일방통행만을 허용하는 반투막과 같다.
그런데 도대체 검은 구멍이 외부의 물체에 어떻게 중력을 미칠 수 있을까? 검은 구멍으로부터는 아무런 정보나 신호도 빠져나올수 없을 터인데도, 이미 붕괴해버린 별의 중력장이 어떻게 검은 구멍 밖으로 탈출할 수 있을까?
사실은 탈출이 아니라 이를테면 "호랑이는 죽어서 가죽을 남기고 별은 죽어서 중력장을 남긴다"는 말이 제격이다. 즉 검은 구멍의 중력장은 사실은 죽기 이전의 별의 중력장이다. 그후 별이 검은 구멍의 중심(특이점)에서 없어졌다해도 밖의 중력장은 이런 변동을 알 길이 없으므로 그대로 남아 있는 셈이다. 별이 죽은 후의 검은 구멍은 자립한 중력장으로 생각할 수 있다. (여기서 죽는다는 말은 R=O을 뜻한다. 이 특이점에서 별이 어떻게 되는지는 오늘날의 이론으로 알 수 없다.)
중력붕괴에 걸리는 시간을 알아보기 위해서 R〉${R}_{G}$에서 물체를 검은 구멍으로 떨어뜨리는 경우를 생각해보자. 이 경우에 유의할 점은 물체와 같이 떨어지는 시계가 재는 고유시간( τ)과 검은 구멍에서 멀리 떨어져서(중력의 영향이 거의 없는) 관측자가 재는 좌표시간(t)를 구별하는 것이다.
물체가 그 위치를 알리기 위해서 고유시간의 일정한 간격(△t)마다 빛이나 전파의 신호를 보내는 것을 관측자가 받아서 자기 시계의 해당하는 시간 △t를 읽는다고 하자. 중력장을 빠져나오는데 드는 에너지의 손실 때문에 빛의 에너지의 감소로 진동수는 작아지므로 주기는 길어진다. 즉 중력장은 시계를 느리게 한다. 상대론에 의한 계산은 놀랍게도 R이 ${R}_{G}$에 가까와짐에 따라 △t→∞로 되어 물체는 ${R}_{G}$까지 가는데 무한히 긴 시간이 걸리게 된다.
떨어지고 있는 물체가 그 크기가 매우 작다면 우주선 안에 무중력상태처럼 바깥중력장의 영향에 관계없이 R=O까지 치닫는다. 표면에서 중심까지 가는 시간은 대략 ${R}_{G}$/C로 계산되어 태양질량의 검은 구멍의 경우 10만분의 1초 정도 걸린다. 물체의 크기가 있을 때는 검은 구멍의 막대한 중력 때문에 깨어지거나 실처럼 가늘게 늘어나지만 걸리는 시간은 별로 차이가 없다.
우리는 검은 구멍에서 멀리 떨어진 외부에서 보고 있기 때문에 별의 표면이 수축하는 것이 R>${R}_{G}$에서 R=${R}_{G}$까지 무한히 긴 시간이 걸리는 것으로 생각될지 모르나 실제는 그렇지 않다. 결국 R<${R}_{G}$인 부분은 이미 죽어버려서 볼 수 없고 R=${R}_{G}$에서 느리게 수축하는 표면의 일부만 보는 셈인데, 이 때 여기서 나오는 빛은 파장이 엄청나게 길어져서 관측되므로 그 밝기는 사실상 0이다. 즉 별이 외부에서는 관측 불능이다.
백조자리 X-1은 블랙홀
외계여행에서 검은 구멍을 만날 위험성은 얼마나 클까? 검은 구멍의 크기 ${R}_{G}$는 별의 질량 M에 비례하고, 또 대개의 별은 태양의 60배를 넘지 않음으로 위험구역의 크기는 지름으로 약 4백km 이하일 것이다.
이것을 가늠할 방법은 검은 구멍의 크기 ${R}_{G}$와 이로부터의 거리 R의 비를 알아 알아보는 것이다. 아인슈타인은 별빛이 태양표면을 스쳐서 지나갈 때 그 중력장의 영향으로 구불어지는 각도 θ=2${R}_{G}$/${R}_{S}$=1″.75로 예측했다. 여기 ${R}_{S}$는 태양반경(7×${10}^{10}$㎝)인데 그의 예측은 1919년 아프리카에서 일어난 개기일식 때 가리워진 태양 옆에 보이는 별의 위치로부터 실증되었다. 이 결과를 검은 구멍에 대해서 거리R로지나가는 빛에 적용해 보면 θ=2${R}_{G}$/R(radian)만큼 구부러지는 셈이다. R=100${R}_{G}$로 하면 θ=$\frac{1}{50}$radian 약1˚로 빛의 진로는 크게 변하지 않으므로 중력반경의 1백배거리는 안전거리로 볼 수 있다. (태양의 경우 3백km)
재미있는 것은 R=1.5${R}_{G}$때 빛은 검은 구멍 둘레에 원을 그리게 되는데 이 원궤도는 불안정해서 조금만 빗나가면 밖으로 뛰쳐 나가거나 안쪽으로 나선을 돌며 구멍으로 빨려 들어간다. ${R}_{G}$에 가까와질수록 더욱 큰 중력을 뚫고 나와야하므로 에너지가 적은(파장이 더 긴) 붉은 빛으로 변해간다.
검은 구멍에 가까이 있는 우주비행사는 이런 빛의 이상한 굴절 때문에 곡면거울로 비쳐보는 듯한 일그러진 풍경을 보게 된다.
검은 구멍은 밤하늘에 보이지 않는 작은 표적이기 때문에 외계여행에서도 찾아내기 어려울 정도인데 검은 구멍의 전신인 초신성(超新星) 폭발의 빈도를 통계적으로 조사하여 우리 은하안에 약 1억개정도 흩어져 있다고 추정되고 있다.
검은 구멍이 그 이웃에 다른 별과 연성(連星)을 이루고 있을 경우에는 찾기가 더 쉽다. 별이 아주 가까울 경우 검은 구멍의 강한 중력에 끌린 개스가 빨려들어가서 고속도로 회전하는 원반을 만드는데 기체의 마찰로 발생하는 열은 고속도 때문에 온도가 1천만 도를 넘어 파장이 매우 짧은 빛, 즉 X선을 발생하게 된다. 수년전에 X선탐지장치를 실은 인공위성으로 이러한 X선천체를 많이 발견했는데 백조자리의 X-1은 연성을 이룬 검은 구멍의 가능성이 많은 것으로 관심을 끌고 있다. 이 연성은 약 6천광년 거리에 있는 푸른 큰별인데(질량 약30배태양) 이 둘레에 보이지 않는 질량 약 1.5배 태양의 천체가 5.5일마다 한번씩 돌고 있으며 그반경은 50km로 추정되고 있다.
검은 구멍을 빨려 들어 가는 개스의 큰 소용돌이는 반경이 1백만km에 달하고 검은 구멍 가까운 곳에서는 도너츠처럼 굵은 단면을 보이는데 구멍의 크기가 수십km에 불과하므로 마치 목욕탕의 물을 바늘구멍으로 빼는 꼴이 된다. 크고 작은 대조가 매우 인상적이 아닐 수 없다.
흰 구멍?
일반상대론의 기본방정식은 뉴튼역학, 양자역학 등의 그것처럼 시간의 부호를 바꿔도 달라지지 않는다. 그러므로 검은 구멍이 일반적으로 물질이나 빛을 빨아들이는 과정을 영화로 찍어서 이것을 거꾸로 돌려서 보는 것도 가능하게 된다. 그러면 검은 구멍과 반대로 일방적으로 물질과 빛을 뱉어내는(빨아 들이지 않는) 이를테면 '흰 구멍'(white hall)이 존재할 수 있다. 그리고 시초에는 시공간의 특이점이 있으므로 이것은 우주시대의 대폭발에 해당하고 여기서는 곡율이∞이고 물질이 파괴되는 대신에 여기서부터 물질이 생성된다.
그런데 이 우주시초의 특이점은 검은 구멍 안의 특이점의 시간을 반전한 것으로 보지 않는다. 그 이유는 전자는 포괄적(包括的)인데 반하여 후자는 국소적(局所的)인 특이점이기 때문이다.
60년대에 소련의 '노비코프'(Novikov)는 우주시초의 대폭발에 참여하지 않는 적은 일부분이 그후에 폭발(소폭발)하였다면 이것은 흰 구멍과 같이 보일 가능성을 지적했다. 그러나 70년대 미국의 '이어들리'(Eardley)는 이 지체된 부분에는 근방의 빛이 대량으로 빨려들어와서 흰 구멍이 될 틈없이 곧(약1/1000초) 검은 구멍으로 둔갑할 가능성을 밝혔다.
영국의 '펜로우즈'(Penrose)는 흰 구멍 폭발의 임의성을 염려하여 그 존재 가능성을 의심하고 있다.
그러나 '퀘이사'(Quaser 별처럼 보이는 원거리의 강한 전파원)의 정체를 이것으로 보는 학자도 있어 아직도 확실한 결론은 없는 것 같다.
'호킹'의 새 이론
검은 구멍은 언제나 별이 죽음으로써만 태어나는 것일까? 검은 구멍을 태어나게 한 원동력은 별 스스로의 중력이었으므로 별보다 가벼운 물체의 경우는 그 자체의 중력을 보강해서 검은 구멍의 크기로 압축할 엄청난 압력이 필요하다. 1g의 물체라면 태양의 경우와 비교해서 ${10}^{-28}$㎝(!) 이런 힘은 오늘날 우주 어디서도 찾아볼 수 없다. 그러나 팽창우주 초기의 고온고밀도의 상태를 돌이켜보면 가벼운 작은 검은 구멍의 가능성은 많다.
이런 가능성에 힘입어 73년 영국의 '호킹'(Hauking)은 검은 구멍의 양자역학을 생각하기 시작했다. 양자역학의 등뼈라 할수 있는 '불확정성 원리'에 의하면 진공이란 아무것도 없는 공간이 아니라 입자와 반입자(反粒子)의 가상적인 쌍이 수많이 들끓고 쉴새없이 요동하는 공간이라는 것에 유의했다. 그러면 검은 구멍의 표면(사상의 지평선) 가까이를 헤매는 이런 입자의 쌍에서 그 한쪽이 검은 구멍으로 끌려 들어가고 나머지 한쪽은 밖으로 튀겨 나갈 가능성이 있지 않을까? 이런 과정은 결국 음(-)의 에너지를 가진 반입자를 끌어들여서 입자를 뱉어냄으로써 전체적으로 검은 구멍의 질량을 입자 하나만큼 사상의 지평선의 벽을 넘어서 밖으로 옮기는 것이므로 보통은 불가능한 일이다. 그러나 이벽이 너무 두껍지 않은 작은 검은 구멍인경우에는 양자역학에서 잘 알려진 '턴넬(t-unnel)효과'에 의해서 가능하게 된다.
이런 생각은 그 때까지 알려졌던 검은 구멍의 개념과는 정반대되는 생각이었으므로 그는 그 결과가 잘못이 아닌지를 되풀이 조사하고 망설이다가 74년에 처음으로 발표하였다. 이것은 바로 '검은 구름의 증발' 또는 '호킹 복사'로 알려지게 된 현상이다.
이것은 마치 흑체복사와 유사하므로 흑체온도에 해당하는 양이 M에 반비례하는 복사로 생각할 수 있는데 M이 작을 수록 T⁴(따라서 ${M}^{-4}$)에 비례해서 커지고 여기에 표면적(∝${R}_{G}^{2}$ ∝M²)을 곱하여 계산하면 검은 구멍이 증발해서 없어지는데 걸리는 시간은 M³에 비례한다.
태양의 경우는 ${10}^{66}$년이므로 우주의 나이 ${10}^{10}$년보다 엄청나게 큰 값이므로 문제가 되지 못하지만, 작은 M인 경우 또는 증발의 마지막 순간에는 광장한 크기의 폭발이 일어나게 된다. 그는 이런 작은 검은 구멍은 짧은 시간 후의 폭발로 인해 작은 흰 구멍과 구별하기 어렵다는 사실을 밝혔다.
우주공간에 존재하는 블랙홀은 빛이나 물질 어느 것도 빠져나오지 못하는 검은 구멍을 말한다. 태양보다 무거운 천체가 강한 중력을 받아 수축되어 어느 한계에 오면 중력이 무한대가 되어, 그 곳에서는 빛 에너지 물질 입자의 어느 것도 빠져나오지 못한다.
검은 구멍(블랙홀)은 아인슈타인의 일반상대성 이론에 근거를 둔 것으로 오랫동안 이론상으로만 존재해왔으나 최근 인공위성에 실어보낸 X선 망원경으로 백조자리에 있는 X-1이라는 X선원(線原)을 발견, 이것이 검은 구멍일 가능성이 확실해 그 실제 가능성이 분명해졌다.
전형적인 검은 구멍이라 할 수 있는 태양의 20배의 질량을 가진 별도 반지름이 10여km로 축소되며 중력은 지구중력의 1백억 배로 엄청나게 크다. 검은 구멍의 수는 우리 은하계 안에 1억개 정도가 있는 것으로 추정된다.
시간과 공간이 역전하는 물리학의 새로운 영역을 차근차근 이론적으로 접근해보자.
이론이 파탄하는 물리학의 종점
지구의 중력을 벗어나서 외계로 우주선을 보내기 위해서는 최소한 약11km/sec의 속도가 필요하다는 것은 잘 알려진 사실이다. 이 속도를 지구로부터의 이탈속도라고 한다. 이탈속도(v)는 천체의 질량(M) 반경(R) 중력상수(G=7×${10}^{-8}$C.G.S.)를 써서 v²=2GM/R로 주어진다. 위의 값은 M, R에 지구의 값을 써서 얻은 것이다.
물체가 가질 수 있는 속도의 한계는 빛의 속도(C=3×${10}^{10}$㎝/sec)이므로 위식에 v대신 C를 넣고 계산한 R의 값(R=2GM/C²)은 빛이나 물체가 이 천체의 중력에서 탈출할 수 있는 한계를 준다. 이것은 그 천체의 중력반경(${R}_{G}$)이라하여 태양의 경우 3km, 지구의 경우 약 1cm가 된다.
이 간단한 계산에서 알 수 있는 사실은 별의 크기가 ${R}_{G}$이하로 작아지면 빛도 빠져나올 수 없으므로 우리는 그 별을 볼 수없다는 것이다. 이런 사실은 이미 1795년에 수학자 '라플라스'(Laplace)가 '뉴튼'(Newton)의 중력이론을 써서 알아냈지만, ${R}_{G}$는 1917년에 '슈바르쯔실트(Schwarzschild)'가 아인슈타인(Einstein)의 중력이론 (일반 상대론)을 써서 얻어낸 한계값과 일치하므로 슈바르쯔실트 반경으로도 불리고 있다.
그는 공으로된 질량M의 둘레에 생기는 중력장(중력이 작용하는 공간)에서 공의 중심에서 ${R}_{G}$인 거리의 안팎에서 시간과 공간의 역할이 서로 뒤바뀌는 이상한 일이 일어나는 사실을 밝혔다.
즉 시간 t와 공간 R을 서로 수직인 두 축으로 잡을 때 R<${R}_{G}$에서는 R축이 t축으로 바뀐다는 것이다. 상대론에서는 1차원의 시간을 합한 4차원의 시공간(時空間)을 생각하는데, 이를테면 물체의 운동을 4차원 시공간의 곡선, 세계선(世界線)으로 나타내고, 일반적으로 물리학을 4차원 시공간의 기하학으로 변환한다.
그런데 공간과 시간과는 근본적으로 다른 점이 있다. 그것은 공간의 방향에서는 상하좌우로 각 공간축의 두 방향을 자유로 택할 수 있으나, 시간의 방향에는 한 방향, 즉 과거에서 현재를 거쳐 미래로 밖에 택할 수 없다는 것이다.
그러므로 R<${R}_{G}$에서 R축이 t축으로 바뀌면 R은 한 방향(이 경우 중심을 향하는)으로 변할 수 밖에 없다. 즉 R=O을 향하는 운명을 피할 길이 없다. 이것은 마치 우리가 늙어가는 운명(시간의 화살)을 돌이킬 수 없는 것과 다름없다.
R=O은 뉴튼역학으로 중력이 ∞(상대론으로는 시공간의 곡률이 ∞)되는 특이점(特異点)이다. 특이점은 이론의 파탄을 일으키는 영역, 즉 물리학의 종점을 가리킨다. 1960년대에 이르러 '휠러(Wheeler)는 ${R}_{G}$이하로 수축되어 빛이 나오지 못하는 천체를 '검은 구멍'(Black hole)으로 이름지었다. 검은 구멍 속의 특이점으로 치닫고야마는 천체의 중력붕괴(重力崩壞)는 물리학에 대한 만만치 않은 도전으로 받아들여지게 되었다.
그런데 보통 크기가 수십만- 수천만㎞에 달하는 별들이 이처럼 작게 수축될수 있을까?

거대질량 별의 마지막 모습
이미 1930년대에 크기가 태양의 1백분의1 정도의 고온의 별(백색외성)이 존재함이 밝혀졌다. 이런 압축된 상태에서는 전자들이 너무 압축된 결과, 같은 상태를 두 전자가 차지할 수 없는 배타원리(排他原理)에 따르는 양자역학적인 압력이 보통의 기체압력( ∝온도, 밀도)을 대신하여 별의 중력을 지탱하는 사실이 알려졌다.
그러나 별의 질량이 태양의 약 1.4배의 한계를 넘어서면 전자의 압력이 아니라 중성자의 압력으로 지탱하게 된다. 이 경우의 밀도는 백색왜성의 1억배가 넘는 원자핵의 밀도(${10}^{14}$g/ ㎤)에 달하고 그 크기는 10km 정도로 압축된다. 1938년에 '오펜하이머'(Oppenheimer) 등에 의해서 이러한 중성자별의 존재가 예견되었다.
1967년에 이르러 처음으로 전파의 펄스를 내는 '펄사'(pulsar)라는 별이 관측되었는데, 전파의 펄스와 빛의 변동이 매우 규칙적인 것으로 미루어 이는 반경이 10km정도의 중성자별이 빠르게 자전하는 것으로 설명되었다. 특히 2개의 펄사는 옛날의 초신성(超新星)이 폭발한 곳에 발견되었으므로 중성자별은 초신성 폭발의 유물로 추정되게 되었다.
그런데 중성자별도 질량이 어느 한계(태양의 3배정도)를 넘으면, 지나친 별의 무게를 지탱할 압력이 없으므로 별은 스스로의 무게 때문에 검은 구멍으로 수축을 할 수 밖에 없게 된다.
결국 별의 일생의 마지막 단계는 그 질량에 따라서 3가지로 나뉘어져서 백색외성(M<;1.4태양) 중성자별(M$\lesssim$3.0태양) 검은 구멍(M>;3.0태양)으로 된다.
일방통행의 반투막
중력반경 ${R}_{G}$의 구면은 외부로 나가는 빛(정보)이나 물체를 일체 차단해버리는 한계면으로 '사상(事象)의 지평선'으로 불린다. 이를 검은 구멍의 표면이라고 생각 할 수 있다. 검은 구멍은 막대한 중력의 수렁이므로 사상의 지평선은 일방통행만을 허용하는 반투막과 같다.
그런데 도대체 검은 구멍이 외부의 물체에 어떻게 중력을 미칠 수 있을까? 검은 구멍으로부터는 아무런 정보나 신호도 빠져나올수 없을 터인데도, 이미 붕괴해버린 별의 중력장이 어떻게 검은 구멍 밖으로 탈출할 수 있을까?
사실은 탈출이 아니라 이를테면 "호랑이는 죽어서 가죽을 남기고 별은 죽어서 중력장을 남긴다"는 말이 제격이다. 즉 검은 구멍의 중력장은 사실은 죽기 이전의 별의 중력장이다. 그후 별이 검은 구멍의 중심(특이점)에서 없어졌다해도 밖의 중력장은 이런 변동을 알 길이 없으므로 그대로 남아 있는 셈이다. 별이 죽은 후의 검은 구멍은 자립한 중력장으로 생각할 수 있다. (여기서 죽는다는 말은 R=O을 뜻한다. 이 특이점에서 별이 어떻게 되는지는 오늘날의 이론으로 알 수 없다.)
중력붕괴에 걸리는 시간을 알아보기 위해서 R〉${R}_{G}$에서 물체를 검은 구멍으로 떨어뜨리는 경우를 생각해보자. 이 경우에 유의할 점은 물체와 같이 떨어지는 시계가 재는 고유시간( τ)과 검은 구멍에서 멀리 떨어져서(중력의 영향이 거의 없는) 관측자가 재는 좌표시간(t)를 구별하는 것이다.
물체가 그 위치를 알리기 위해서 고유시간의 일정한 간격(△t)마다 빛이나 전파의 신호를 보내는 것을 관측자가 받아서 자기 시계의 해당하는 시간 △t를 읽는다고 하자. 중력장을 빠져나오는데 드는 에너지의 손실 때문에 빛의 에너지의 감소로 진동수는 작아지므로 주기는 길어진다. 즉 중력장은 시계를 느리게 한다. 상대론에 의한 계산은 놀랍게도 R이 ${R}_{G}$에 가까와짐에 따라 △t→∞로 되어 물체는 ${R}_{G}$까지 가는데 무한히 긴 시간이 걸리게 된다.
떨어지고 있는 물체가 그 크기가 매우 작다면 우주선 안에 무중력상태처럼 바깥중력장의 영향에 관계없이 R=O까지 치닫는다. 표면에서 중심까지 가는 시간은 대략 ${R}_{G}$/C로 계산되어 태양질량의 검은 구멍의 경우 10만분의 1초 정도 걸린다. 물체의 크기가 있을 때는 검은 구멍의 막대한 중력 때문에 깨어지거나 실처럼 가늘게 늘어나지만 걸리는 시간은 별로 차이가 없다.
우리는 검은 구멍에서 멀리 떨어진 외부에서 보고 있기 때문에 별의 표면이 수축하는 것이 R>${R}_{G}$에서 R=${R}_{G}$까지 무한히 긴 시간이 걸리는 것으로 생각될지 모르나 실제는 그렇지 않다. 결국 R<${R}_{G}$인 부분은 이미 죽어버려서 볼 수 없고 R=${R}_{G}$에서 느리게 수축하는 표면의 일부만 보는 셈인데, 이 때 여기서 나오는 빛은 파장이 엄청나게 길어져서 관측되므로 그 밝기는 사실상 0이다. 즉 별이 외부에서는 관측 불능이다.
백조자리 X-1은 블랙홀
외계여행에서 검은 구멍을 만날 위험성은 얼마나 클까? 검은 구멍의 크기 ${R}_{G}$는 별의 질량 M에 비례하고, 또 대개의 별은 태양의 60배를 넘지 않음으로 위험구역의 크기는 지름으로 약 4백km 이하일 것이다.
이것을 가늠할 방법은 검은 구멍의 크기 ${R}_{G}$와 이로부터의 거리 R의 비를 알아 알아보는 것이다. 아인슈타인은 별빛이 태양표면을 스쳐서 지나갈 때 그 중력장의 영향으로 구불어지는 각도 θ=2${R}_{G}$/${R}_{S}$=1″.75로 예측했다. 여기 ${R}_{S}$는 태양반경(7×${10}^{10}$㎝)인데 그의 예측은 1919년 아프리카에서 일어난 개기일식 때 가리워진 태양 옆에 보이는 별의 위치로부터 실증되었다. 이 결과를 검은 구멍에 대해서 거리R로지나가는 빛에 적용해 보면 θ=2${R}_{G}$/R(radian)만큼 구부러지는 셈이다. R=100${R}_{G}$로 하면 θ=$\frac{1}{50}$radian 약1˚로 빛의 진로는 크게 변하지 않으므로 중력반경의 1백배거리는 안전거리로 볼 수 있다. (태양의 경우 3백km)
재미있는 것은 R=1.5${R}_{G}$때 빛은 검은 구멍 둘레에 원을 그리게 되는데 이 원궤도는 불안정해서 조금만 빗나가면 밖으로 뛰쳐 나가거나 안쪽으로 나선을 돌며 구멍으로 빨려 들어간다. ${R}_{G}$에 가까와질수록 더욱 큰 중력을 뚫고 나와야하므로 에너지가 적은(파장이 더 긴) 붉은 빛으로 변해간다.
검은 구멍에 가까이 있는 우주비행사는 이런 빛의 이상한 굴절 때문에 곡면거울로 비쳐보는 듯한 일그러진 풍경을 보게 된다.
검은 구멍은 밤하늘에 보이지 않는 작은 표적이기 때문에 외계여행에서도 찾아내기 어려울 정도인데 검은 구멍의 전신인 초신성(超新星) 폭발의 빈도를 통계적으로 조사하여 우리 은하안에 약 1억개정도 흩어져 있다고 추정되고 있다.
검은 구멍이 그 이웃에 다른 별과 연성(連星)을 이루고 있을 경우에는 찾기가 더 쉽다. 별이 아주 가까울 경우 검은 구멍의 강한 중력에 끌린 개스가 빨려들어가서 고속도로 회전하는 원반을 만드는데 기체의 마찰로 발생하는 열은 고속도 때문에 온도가 1천만 도를 넘어 파장이 매우 짧은 빛, 즉 X선을 발생하게 된다. 수년전에 X선탐지장치를 실은 인공위성으로 이러한 X선천체를 많이 발견했는데 백조자리의 X-1은 연성을 이룬 검은 구멍의 가능성이 많은 것으로 관심을 끌고 있다. 이 연성은 약 6천광년 거리에 있는 푸른 큰별인데(질량 약30배태양) 이 둘레에 보이지 않는 질량 약 1.5배 태양의 천체가 5.5일마다 한번씩 돌고 있으며 그반경은 50km로 추정되고 있다.
검은 구멍을 빨려 들어 가는 개스의 큰 소용돌이는 반경이 1백만km에 달하고 검은 구멍 가까운 곳에서는 도너츠처럼 굵은 단면을 보이는데 구멍의 크기가 수십km에 불과하므로 마치 목욕탕의 물을 바늘구멍으로 빼는 꼴이 된다. 크고 작은 대조가 매우 인상적이 아닐 수 없다.
흰 구멍?
일반상대론의 기본방정식은 뉴튼역학, 양자역학 등의 그것처럼 시간의 부호를 바꿔도 달라지지 않는다. 그러므로 검은 구멍이 일반적으로 물질이나 빛을 빨아들이는 과정을 영화로 찍어서 이것을 거꾸로 돌려서 보는 것도 가능하게 된다. 그러면 검은 구멍과 반대로 일방적으로 물질과 빛을 뱉어내는(빨아 들이지 않는) 이를테면 '흰 구멍'(white hall)이 존재할 수 있다. 그리고 시초에는 시공간의 특이점이 있으므로 이것은 우주시대의 대폭발에 해당하고 여기서는 곡율이∞이고 물질이 파괴되는 대신에 여기서부터 물질이 생성된다.
그런데 이 우주시초의 특이점은 검은 구멍 안의 특이점의 시간을 반전한 것으로 보지 않는다. 그 이유는 전자는 포괄적(包括的)인데 반하여 후자는 국소적(局所的)인 특이점이기 때문이다.
60년대에 소련의 '노비코프'(Novikov)는 우주시초의 대폭발에 참여하지 않는 적은 일부분이 그후에 폭발(소폭발)하였다면 이것은 흰 구멍과 같이 보일 가능성을 지적했다. 그러나 70년대 미국의 '이어들리'(Eardley)는 이 지체된 부분에는 근방의 빛이 대량으로 빨려들어와서 흰 구멍이 될 틈없이 곧(약1/1000초) 검은 구멍으로 둔갑할 가능성을 밝혔다.
영국의 '펜로우즈'(Penrose)는 흰 구멍 폭발의 임의성을 염려하여 그 존재 가능성을 의심하고 있다.
그러나 '퀘이사'(Quaser 별처럼 보이는 원거리의 강한 전파원)의 정체를 이것으로 보는 학자도 있어 아직도 확실한 결론은 없는 것 같다.
'호킹'의 새 이론
검은 구멍은 언제나 별이 죽음으로써만 태어나는 것일까? 검은 구멍을 태어나게 한 원동력은 별 스스로의 중력이었으므로 별보다 가벼운 물체의 경우는 그 자체의 중력을 보강해서 검은 구멍의 크기로 압축할 엄청난 압력이 필요하다. 1g의 물체라면 태양의 경우와 비교해서 ${10}^{-28}$㎝(!) 이런 힘은 오늘날 우주 어디서도 찾아볼 수 없다. 그러나 팽창우주 초기의 고온고밀도의 상태를 돌이켜보면 가벼운 작은 검은 구멍의 가능성은 많다.
이런 가능성에 힘입어 73년 영국의 '호킹'(Hauking)은 검은 구멍의 양자역학을 생각하기 시작했다. 양자역학의 등뼈라 할수 있는 '불확정성 원리'에 의하면 진공이란 아무것도 없는 공간이 아니라 입자와 반입자(反粒子)의 가상적인 쌍이 수많이 들끓고 쉴새없이 요동하는 공간이라는 것에 유의했다. 그러면 검은 구멍의 표면(사상의 지평선) 가까이를 헤매는 이런 입자의 쌍에서 그 한쪽이 검은 구멍으로 끌려 들어가고 나머지 한쪽은 밖으로 튀겨 나갈 가능성이 있지 않을까? 이런 과정은 결국 음(-)의 에너지를 가진 반입자를 끌어들여서 입자를 뱉어냄으로써 전체적으로 검은 구멍의 질량을 입자 하나만큼 사상의 지평선의 벽을 넘어서 밖으로 옮기는 것이므로 보통은 불가능한 일이다. 그러나 이벽이 너무 두껍지 않은 작은 검은 구멍인경우에는 양자역학에서 잘 알려진 '턴넬(t-unnel)효과'에 의해서 가능하게 된다.
이런 생각은 그 때까지 알려졌던 검은 구멍의 개념과는 정반대되는 생각이었으므로 그는 그 결과가 잘못이 아닌지를 되풀이 조사하고 망설이다가 74년에 처음으로 발표하였다. 이것은 바로 '검은 구름의 증발' 또는 '호킹 복사'로 알려지게 된 현상이다.
이것은 마치 흑체복사와 유사하므로 흑체온도에 해당하는 양이 M에 반비례하는 복사로 생각할 수 있는데 M이 작을 수록 T⁴(따라서 ${M}^{-4}$)에 비례해서 커지고 여기에 표면적(∝${R}_{G}^{2}$ ∝M²)을 곱하여 계산하면 검은 구멍이 증발해서 없어지는데 걸리는 시간은 M³에 비례한다.
태양의 경우는 ${10}^{66}$년이므로 우주의 나이 ${10}^{10}$년보다 엄청나게 큰 값이므로 문제가 되지 못하지만, 작은 M인 경우 또는 증발의 마지막 순간에는 광장한 크기의 폭발이 일어나게 된다. 그는 이런 작은 검은 구멍은 짧은 시간 후의 폭발로 인해 작은 흰 구멍과 구별하기 어렵다는 사실을 밝혔다.











