d라이브러리

지구에서 달을 바라보니 새롭게 느껴져. 내가 사는 달과 지구의 크기는 얼마나 다를까? 보름달이 아닌 초승달 모양의 넓이도 구할 수 있을까?

내 궁금증을 해결해 준다면 달에서 직접 절구를 찧어 만든 달떡을 줄게~.

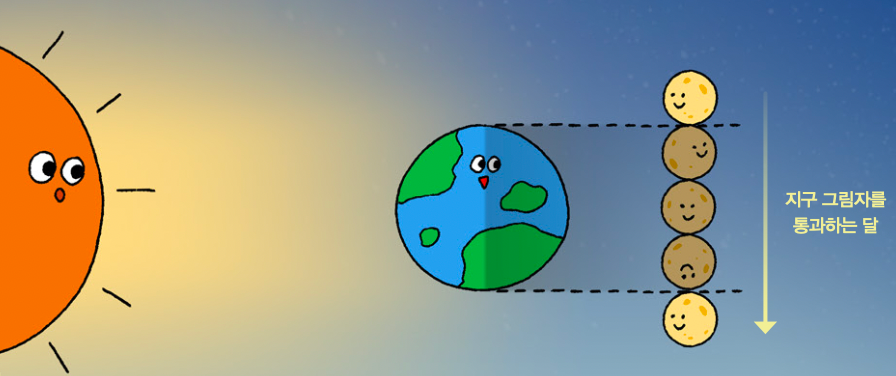
지구의 그림자를 통과한 달

지구와 달의 실제 크기를 몰라도 그 크기를 비교할 수 있을까요? 지금으로부터 약 2300년 전, 고대 그리스의 수학자이자 천문학자인 아리스타르코스는 지구의 ‘그림자’를 이용해 지구와 달의 크기를 비교했어요. 바로 월식^★에서 방법을 떠올렸지요.

먼저, 아리스타르코스는 달이 지구 그림자에 가려지기 시작하는 때부터 시간을 쟀어요. 달이 지구 그림자에 완전히 가려져 보이지 않게 될 때까지 얼마나 걸리는지 측정했지요. 달의 크기가 클수록 그림자에 가려지는 데 걸리는 시간이 길어질 거라고 생각한 거예요.

그다음, 달이 지구 그림자에 완전히 가려진 때부터 다시 그림자를 완전히 빠져나올 때까지의 시간을 쟀어요. 지구의 크기가 클수록 지구의 그림자도 커지기 때문에 달이 지구 그림자를 통과하는 데 걸리는 시간도 길어질 거라고 생각했지요.

이렇게 계산한 결과, 아리스타르코스는 지구 크기에 대한 달 크기의 비율^★이 약 (=0.333…)이라는 걸 알아냈어요. 기술이 발전한 뒤 관측한 결과, 실제로 달의 둘레는 10921km, 지구 둘레는 40075km였어요. 지구 크기에 대한 달 크기의 비율은 10921/40075(=약 0.27)이지요. 관측 기술이 발달하지 않았을 때 구한 값인데도 크게 다르지 않아요.

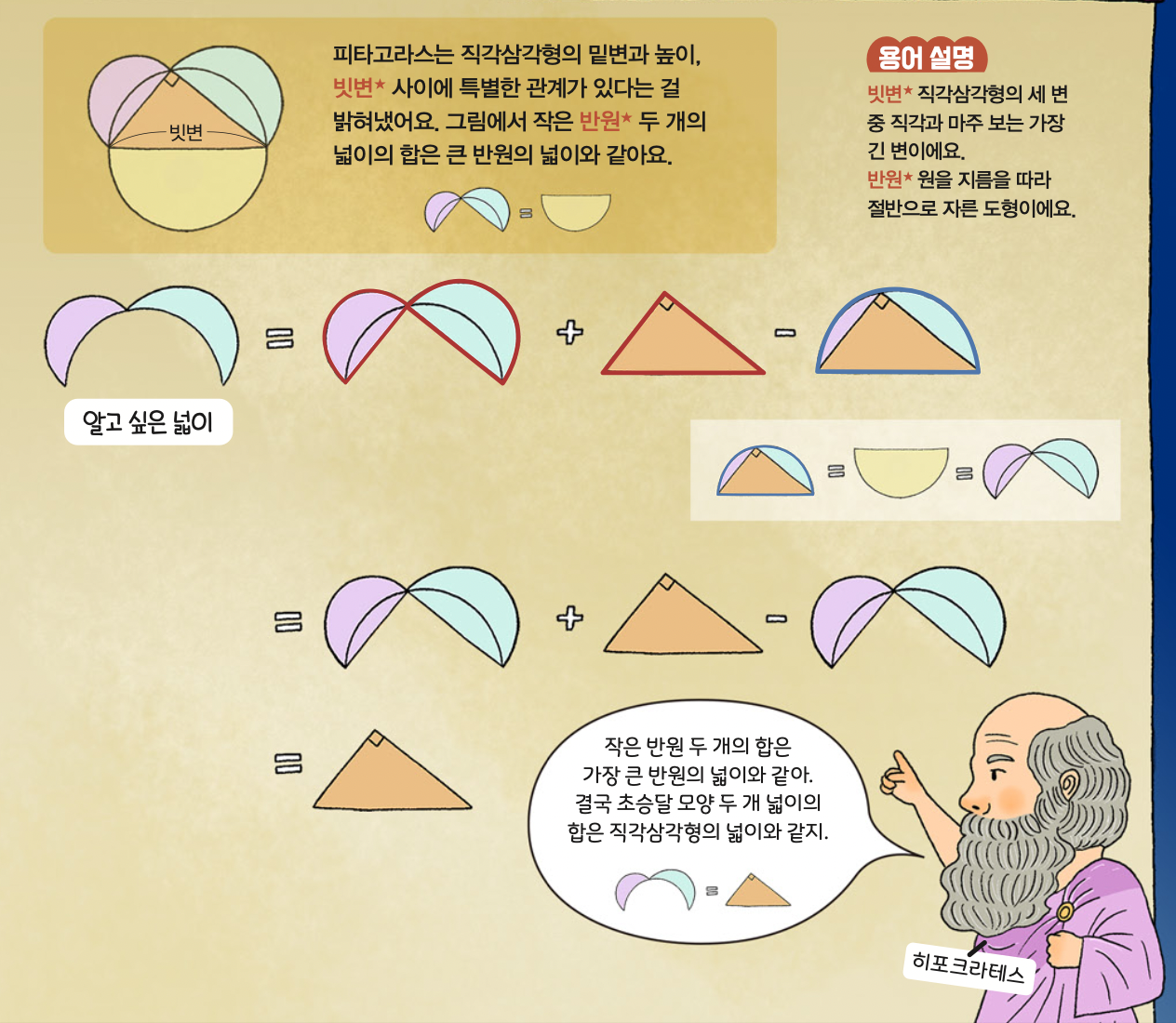
히포크라테스의 초승달

지금으로부터 약 2500년 전, 고대 그리스의 수학자 히포크라테스는 초승달 모양 도형의 넓이가 궁금했어요. 하지만 곡선으로 이뤄진 도형은 자로 재서 넓이를 구하기 어려웠지요. 그래서 직선으로 이뤄져 있으면서도 초승달 모양과 넓이가 같은 도형을 찾아냈어요. 바로 직각삼각형이에요. 히포크라테스는 ‘피타고라스의 정리’를 이용해 초승달 모양의 넓이와 직각삼각형의 넓이 사이에 특별한 법칙이 있다는 걸 알아냈지요.

용어 설명

월식^★ 지구가 태양과 달 사이에 위치해, 달이 지구의 그림자에 가려지는 현상이에요.

비율^★ 기준량에 대한 비교하는 양의 크기를 말해요.