d라이브러리

팬케이크를 여러 장 굽다 보면 크기가 제각각이다. 항상 일정한 크기로 팬케이크를 구우면 좋으련만 생각보다 쉽지 않다. 팬케이크를 다 굽고 접시에 쌓아 올려놓고 보니 큰 것이 맨 위에 올라와 있어 먹음직스럽지 않아 보인다. 크기가 가장 큰 것을 맨 아래에 가장 작은 것을 맨 위에 놓기 위해선 팬케이크를 최소 몇 번 뒤집어야 할까?

이 문제를 떠올린 주인공은 미국 수학자 제이콥 굿맨이다. 그는 1975년 어느 날 수건을 개어 쌓던 중 마지막 더미가 엉망인 것을 보고 접어둔 수건을 크기에 맞게 다시 정렬해야겠다고 생각했다. 크기가 큰 수건이 아래에, 작은 수건이 위에 오도록 말이다. 그런데 이미 방이 가득 차서 새로 더미를 놓을 자리가 없었다. 굿맨은 이미 만든 수건 더미를 뒤집어 가며 크기순으로 정렬하기로 했다. 그러는 동안 흥미로운 질문이 떠올랐다. 

‘최악의 경우 몇 번이나 뒤집어야 차례대로 정렬할 수 있을까?’ 

굿맨은 이 문제를 수건에서 팬케이크로 바꿔 미국의 수학 학술지 ‘미국 월간 수학’에 보냈다. 재미있는 건, 자신의 이름 대신 ‘해리 드웨이터’라는 가명을 써서 보냈다. 당시 한창 수학자로서 명성을 쌓아가던 굿맨은 사람들이 자신을 하찮은 퍼즐에나 관심 있는 수학자라 생각할까 봐 이름을 바꿨다고 한다. 하지만 그의 우려와 달리 팬케이크 문제는 수학자 사이에서 난제로 유명해지면서 여러 파생 연구를 낳았다. 

문제를 쉽게 이해하기 위해 팬케이크가 3장 있을 때를 살펴보자. 크기가 다른 3장의 팬케이크가 쌓여 있는 경우의 수는 아래 그림처럼가지다. 각각 몇 번 만에 순서대로 놓을 수 있을까? 

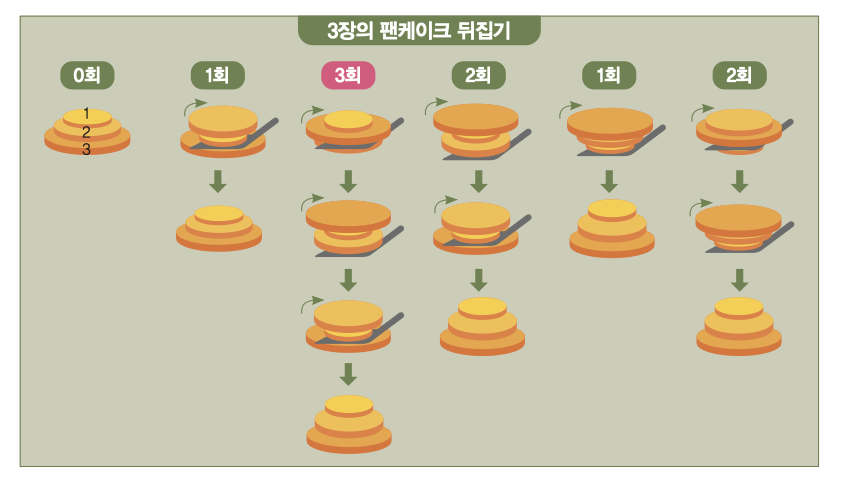
먼저 첫 번째는 기준값으로, 이미 순서대로 정렬돼 있으므로 뒤집는 수는 0이다. 두 번째 경우에는 위에서 두 번째 팬케이크에 뒤집개를 넣어 위아래로 뒤집으면 한 번에 정렬되므로 뒤집는 수는 1이다. 같은 방법으로 나머지 팬케이크도 따져보면, 3장의 팬케이크 문제의 뒤집는 수는 3이라는 것을 알 수 있다. 팬케이크 문제의 뒤집는 수는 최소 횟수 중에 가장 큰 수를 기준으로 한다.

빌 게이츠도 도전한 팬케이크 문제

팬케이크 수가 늘어나면 훨씬 더 문제가 어려워진다. 그렇다면 n장일 때 팬케이크를 뒤집는 최소 횟수를 바로 계산할 수 있는 일반화 방법이 있을까? 

많은 수학자가 이 방법을 찾기 위해 팬케이크 문제를 연구했다. 그중에는 마이크로소프트 설립자 빌 게이츠도 있다. 게이츠는 미국 하버드대학교 수학과 출신인데, 유일하게 남긴 수학 논문이 바로 팬케이크 문제에 관한 것이다. 게이츠는 1979년 발표한 논문에서 팬케이크가 n장일 때의 최소 뒤집는 수의 상한값을 (5n+5)/3로 제시했다. 이후 30년이나 지난 2009년 미국 텍사스대학교 연구팀이 18n/11으로 개선했다. 

하지만 이것이 정확한 답은 아니다. 이후 후속 연구가 계속 나왔지만, 더 효율적인 방법으로 줄여나갈 뿐, 정확한 답을 찾지 못했다. 그 이유는 2011년에 밝혀졌다. 프랑스 국립과학연구센터(CNRS)의 로랑 뷜토, 기욤 페르틴, 이레나 루수는 ‘팬케이크 뒤집기는 어렵다’라는 제목의 논문에서 팬케이크 문제가 다항식으로 나타낼 수 있는 단계 안에 정답을 찾는 효율적인 알고리듬이 없는 ‘NP-난해’라는 것을 증명했다. ‘NP-난해’는 경우의 수를 일일이 직접 따져보는 것 말고는 수학적으로 일반화한 답을 찾을 수 없는 문제를 뜻한다. 

정확한 일반식을 구할 순 없지만, 팬케이크 문제의 원리는 불규칙한 데이터를 정렬하는 컴퓨터과학에서 필요해 더 효율적인 알고리듬을 찾는 연구는 계속 이어지고 있다. 

또 ‘까맣게 탄 면이 있는 팬케이크가 섞여 있을 때 크기가 큰 팬케이크가 아래로 가되 항상 탄 면은 바닥 면이 되도록 배열해야 한다’는 상황을 추가한 ‘탄 팬케이크 문제’, 팬케이크 대신 인도 빵인 로띠로 변형하고 ‘처음에 한 더미로 쌓여 있던 로띠를 불에 구워가며 정렬한다’는 규칙을 추가한 ‘쌍둥이 팬케이크 쌓기 문제’ 같은 발전형 문제가 생겨 여러 분야에 활용되고 있다.