선택 공리는 여러 집합의 모임이 주어졌을 때, 각 집합에서 원소를 하나씩 선택할 수 있다는 거예요. 이는 자명해 보이지만 이 정의를 인정하는 순간, 수많은 기이한 결론이 도출됩니다. 한 가지 사례가 앞서 알아본 ‘바나흐-타르스키 정리’였어요. 오늘은 선택 공리가 제기하는 또 다른 수수께끼를 살펴볼게요.

수학에선 이미 증명된 정리로부터 새로운 정리를 증명합니다. 따라서 논증의 단계를 되짚으면 언젠가는 증명 없이 사용할 수밖에 없는 최초의 전제에 다다르지요. 현대 수학은 9개의 전제를 사용하는데, 그 중 하나가 선택 공리입니다.
어떤 집합이 주어졌을 때, 우리는 집합의 원소들에 순서를 부여할 수 있습니다. 예를 들어 집합 {apple, banana, pear}을 생각해 봅시다. 이 원소들을 글자 길이가 짧은 순으로 정렬할 수 있습니다. pear, apple, banana 순이 되겠네요. 다른 순서도 가능합니다. 알파벳 순서대로 정렬하면 apple, banana, pear 순이고, 알파벳 ‘p’가 나타나는 횟수가 적은 것부터 정렬하면 banana, pear, apple 순입니다.
수식으로 정리해 볼까요? 글자 길이 순서를 기호로 ‘→len’, 알파벳 순서를 ‘→abc’, p가 나타나는 횟수의 순서를 ‘→p’로 표기할게요. 그러면 다음과 같습니다.

♥ 실수 집합은 정렬 순서를 가질까?
이번에는 정수 집합을 생각해 볼게요. 우리가 일반적으로 정수에 부여하는 크기 순서는 다음과 같습니다. 이를 ‘ →a’로 표기할게요.
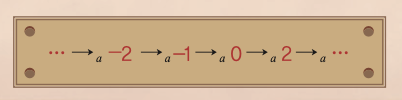
다른 순서 ‘ →b’ 도 가능합니다. 0부터 절댓값의 크기순으로 하나씩 나열하는데, 절댓값의 크기가 같으면 양수가 음수 앞에 오도록 정렬한 겁니다.

그런데 여기서 주목할 점이 있습니다. 순서 →a의 경우 어떤 부분 집합은 순서가 가장 빠른 원소인 최소 원소를 가지지 않습니다. 예를 들어 양의 정수의 집합 {1, 2, 3, 4, ...}은 최소 원소 1을 가지지만, 음의 정수의 집합 {-1, -2, -3, -4, ...}은 최소 원소를 가지지 않습니다. 그러나 순서 →b의 경우 모든 부분 집합이 최소 원소를 가집니다. 양의 정수 집합의 최소 원소는 1이고, 음의 정수 집합의 최소 원소는 -1이지요. 순서 →b와 같이 최소 원소가 항상 존재하는 순서를 ‘정렬 순서’라고 부릅니다. 이제 오늘의 수수께끼가 나갑니다.

실수 집합은 정렬 순서를 가집니다. 그런데 정말 이상하게도 실수 집합의 정렬 순서가 어떻게 생겼는지는 알 수 없습니다! 다시 말해 실수 집합의 정렬 순서는 존재하지만 찾을 수 없습니다.
◆ 선택 공리의 비구성적 논증
이런 괴이한 결론이 발생한 원인은 선택 공리 때문입니다. 선택 공리는 ‘원소를 하나씩 선택할 수 있다’고만 말할 뿐, 어떤 방식으로 선택해야 하는지 알려주지 않습니다. 이같이 가능성만 보장하고 구체적인 내용은 알려주지 않는 진술을 ‘비구성적’이라고 부릅니다.
실수 집합이 정렬 순서를 가지는지 보이기 위해서는 선택 공리가 반드시 필요한데요. 선택 공리가 비구성적이기 때문에 결론 또한 비구성적이 돼버렸습니다. 실수 집합이 정렬 순서라는 것을 알았는데, 어떤 방식으로 순서를 매겨야 하는지는 모르는 판국이 된 것이지요.
비구성적 논증이 어떻게 생겼는지 한 가지 퍼즐로 설명해 볼게요. a와 b가 무리수일 때, ab가 유리수 일까요? 정답은 ‘그럴 수 있다’입니다.
a = b = √2라고 합시다. 그럼 ab =√2√2 입니다. 만약 √2√2가 유리수라면 우리는 원하던 경우를 찾았습니다. 그런데 √2√2가 무리수라면 어떨까요?
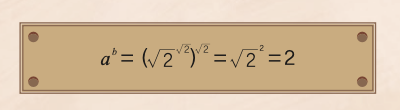
(√2√2 )√2 는 밑과 지수가 모두 무리수인 유리수입니다. 이 논증은 틀리지 않았지만, 찝찝한 구석이 있습니다. 결국 우리가 찾고자 하는 ab가 (√2√2 )√2인지, (√2)√2인지 알려주지 않기 때문입니다. 선택 공리를 사용하는 논증은 대개 이런 비구성적 성격을 지닙니다.
선택 공리에 대한 의견이 분분했던 20세기 초, 수학자들은 선택 공리가 초래하는 비구성적 논증을 받아들여야 하는지에 관해 격론을 벌였습니다. 네덜란드 수학자 라위트전 브라우어르와 프랑스 수학자 앙리 푸앵카레를 필두로 한 일부 수학자는 ‘선택 공리는 지나친 추상화로 인한 내용 없는 정의’라며, ‘직관주의’ 수학을 주장했습니다. 반면, 독일 수학자 다비트 힐베르트를 필두로 한 일부 수학자는 ‘논리적으로 증명되면 참이다’를 구호로 내세워, ‘형식주의’ 수학을 주장했습니다. 그들은 선택 공리가 심각한 모순을 일으키지 않는 선에서 수학 체계를 더 풍부하게 만든다면, 선택 공리는 인정하는 것이 바람직하다고 생각했어요.
이 논쟁에서 누가 승리를 거두었을까요? 아무래도 형식주의가 승리했다고 봐야겠네요. 대다수의 수학자는 선택 공리를 인정할 뿐만 아니라, 비구성적 논증도 왕왕 사용하니까요. 그러나 선택 공리와 비구성적 논증이 제기하는 수수께끼는 여전히 수학, 논리학, 그리고 철학의 난제로 남아 있습니다.