d라이브러리

우주선의 초기 속력 계산, 망원경 렌즈 설계 등 이차방정식을 활용한 실생활 문제는 많이 있어요. 문제 속 이차방정식의 해를 구하기 위해서는 문제의 뜻을 잘 이해하고 구하고자 하는 값을 미지수로 정한 뒤 해를 구하면 되는데요. 해를 구하는 방법이 여러 개라 골라 푸는 즐거움이 있답니다.

중학교 3학년 ‘이차방정식’ 단원에서는 이전에 배운 다항식의 연산과 일차방정식의 풀이법을 활용해서 해를 구할 수 있어요. 그동안 갈고닦은 수학 실력으로 이차방정식을 풀어봐요.

이차방정식 활용의 대표 유형 문제를 위 3가지 방법 중 어떤 것으로 풀지 생각해 봐요.

STEP 1 미지수 설정하기

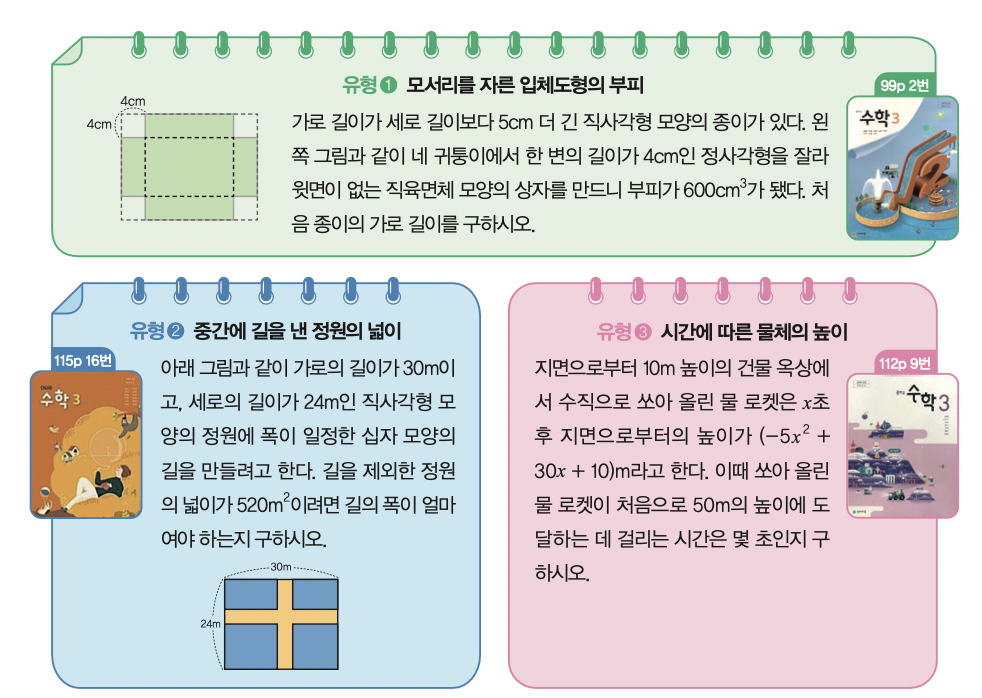
문제에서 구해야 하는 값은 ‘처음 종이의 가로 길이’이므로 이 값을 미지수 x로 정합니다.

STEP 2 이차방정식 세우기

처음 종이의 가로 길이가 xcm이면 세로 길이는 가로 길이보다 5cm만큼 더 짧으므로 (x - 5)cm예요. 네 귀퉁이에서 한 변의 길이가 4cm인 정사각형을 잘라냈으므로, 자른 후 남은 직사각형의 가로 길이는 (x - 8)cm, 세로 길이는 (x - 13)cm가 돼요. 이때 가운데 직사각형을 밑면으로 하고, 높이가 4cm인 직육면체의 부피가 600cm³이므로 부피에 대한 식은 4(x -8)(x - 13) = 600이에요.

STEP 3 인수분해해 이차방정식 풀기

위에서 세운 부피에 대한 식을 정리하고, 모든 항을 좌변으로 이항해요.

4(x² - 21x + 104) = 600

x² - 21x + 104 = 150

x² - 21x - 46 = 0

앞서 말한 해를 구하는 방법 중 (일차식)² = 상수 꼴로 만드는 방법은 풀기 어려워요.
하지만 -23 × 2를 하면 -46이 나오고, -23 + 2을 하면 –21이 나오므로 이차방정식을 인수분해하면 쉽게 풀 수 있어요. 근의 공식으로도 풀 수 있지만 여기서는 인수분해를 이용할게요.

이차방정식을 인수분해하면 x² - 21x - 46 = (x + 2)(x - 23) = 0이므로 이를 만족하는 x는 -2 또는  23이 돼요. x는 길이이기 때문에 음수가 될 수 없어 구하고자 하는 처음 종이의 가로의 길이는 23cm예요.