d라이브러리

짝수 치환과 홀수 치환

양의 정수 n에 대해, 1부터 n까지의 정수들을 모아놓은 집합을 X_n이라고 하자. 이때 X_n의 원소들을 차례대로 나열하는 방법을 ‘치환(permutation)’이라고 부른다. 하나의 치환은 Xn에서 Xn으로 가는 일대일 대응으로 생각할 수 있고, 따라서 하나의 함수 σ:X_n→X_n로도 이해할 수 있다. 치환을 표기하는 방법에는 여러 가지가 있으나, 일반적으로 다음과 같은 기호를 사용한다.

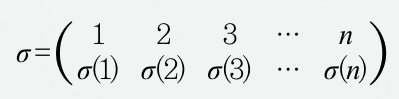
예를 들어, 1을 3으로, 2를 1로, 3을 2로 보내는 치환은

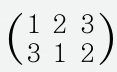
가 된다. 이제 양의 정수 n에 대한 모든 치환들을 모아놓은 집합을 S_n이라 하면, S_n의 원소의 개수는 n!임을 쉽게 알 수 있다. 또한 치환은 함수로 이해할 수 있으므로, S_n에 속하는 임의의 두 치환 σ, γ에 대해 합성합수 σ。γ를 생각할 수 있고, 이 함수도 S_n의 원소가 된다.

어떤 치환이 X_n의 원소들 중 a₁, a₂, a₃, … , a_k에 대해서는 a₁을 a₂, a₂를 a₃, a_k-1을 a_k, a_k를 a₁로 보내고, 나머지 원소들은 자기자신으로 보낼 때, 이 치환을 길이가 k인 ‘순환치환(cycle)’이라고 부른다. 특히 길이가 2인 순환치환을 ‘호환(transposition)’이라고 부른다. 순환치환은 더 간단하게 (a₁a₂a₃…a_k)와 같은 기호로 나타내기도 한다.

치환은 많은 학생이 경우의 수를 찾는 문제나 사다리타기 등에서 접하는 친숙한 개념이다. 또 대수학의 연구 분야 중 하나인 군(group)에서 핵심적인 역할을 한다.

문제①-1 임의의 치환은 호환들의 합성으로 나타낼 수 있음을 보여라.

문제①-2 S_n의 항등치환(즉, X_n의 각각의 원소들을 자기 자신으로 보내는 치환)은 홀수개 호환의 합성으로 나타낼 수 없음을 보여라. 이를 이용해 짝수 개 호환의 합성으로 나타낼 수도 있고 홀수 개 호환의 합성으로도 나타낼 수 있는 치환은 존재하지 않음을 보여라.

문제② S_n의 임의의 치환은 자기 자신을 n!번 합성하면 항등치환이 됨을 보여라.

문제③ 다음과 같은 4×4 숫자퍼즐이 주어져있다. 그림A에서 시작해, 비어있는 칸으로 숫자들을 상하좌우로 한 번씩 움직이는 작업을 진행한다고 할 때, 그림B를 완성할 수 있는지 없는지 판별하라.

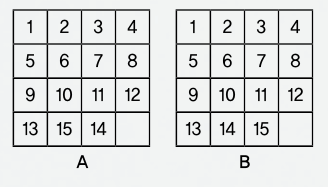
문제④ 소수 p가 p≡2(mod3)을 만족하고, Sp의 원소 σ가 X_p의 원소인 임의의 x에 대해 σ(x)≡x3(modp)가 성립하도록 주어져 있다. 이 때, σ가 짝수 개 호환의 합성으로 나타낼 수 있는 치환이 되도록 하는 p를 모두 구하라. (단, a를 b로 나눈 나머지가 c일 때, a≡c(modb)라고 표기한다.)

현윤석 교수의 팁
S_n의 임의의 치환은 서로 겹치는 원소가 없는 순환치환들의 합성으로 나타낼 수 있음을 먼저 보이세요.

속이 빈 단색 삼각형

100 이상의 정수 n에 대해 평면에 2n개의 점이 배치돼 있다. 이때 평면에 있는 임의의 세 점은 한 직선 위에 있지 않다. 또 n개의 점은 빨간색, n개의 점은 파란색으로 색칠했다. 2n개의 점 중 세 개의 같은 색 점을 꼭짓점으로 하고, 내부에 다른 점이 없는 삼각형을 ‘속이 빈 단색 삼각형’이라고 하자.

문제① 어떤 상수 c1＞0이 있을 때, 어떤 점 배치에 대해서도 속이 빈 단색 삼각형의 개수는 항상 c1n  이상임을 보여라.

문제② 어떤 상수 c₂＞0과 α＞1이 있을 때, 어떤 점 배치에 대해서도 속이 빈 단색 삼각형의 개수는 항상  c₂n^α 이상임을 보여라.

문제③ 어떤 상수 c₃＞0이 있을 때, 어떤 점 배치에 대해서도 속이 빈 단색 삼각형의 개수가 항상 c₃n² 이상임을 증명할 수 있을까?

백진언 연구원의 팁
지수가 2인 경우는 아직 풀리지 않은 문제입니다. 지수가 1이거나 1보다 큰 경우를 먼저 증명해보고, 다양한 전략의 장단점을 분석해서 증명을 강화시켜 나가면 난제를 증명할 수 있지 않을까요?

폴리매스 친구를 만나다!

폴리매스 홈페이지에서 활발히 활동하는 친구를 한 명씩 만나봅니다. 이번 주인공은 꾸준히 함께 풀고 싶은 문제 코너에서 활발하게 활동하는 ‘원형파이’ 친구입니다!

Q 자기 소개 부탁해요!

원주율 π는 원의 지름에 대한 둘레의 비율을 나타내는 수학 상수입니다. 폴리매스 홈페이지에서 닉네임에 파이를 넣는 것이 유행했을 때 제 닉네임을 원형파이로 지었고, 지금까지도 계속 쓰고 있어요.

Q 어떤 계기로 폴리매스에 관심을 가지게 됐나요?

처음에는 폴리매스라는 공간이 어색하고 수학동아에 매달 나오는 폴리매스 문제가 어렵게 느껴졌어요. 그러다가 2020년 5월호에 폴리매스에 대한 기획 기사가 실렸는데, 그 기사를 읽고 ‘함께 풀고 싶은 문제’라는 게시판을 알게 됐어요. 함께 풀고 싶은 문제에 유익하고 좋은 문제가 많은 것을 보고 저도 그런 문제를 내야겠다고 생각했어요. 제가 낸 문제를 누군가가 풀어주거나, 다른 사람들이 낸 문제를 해결해 스티커를 받으면 정말 뿌듯합니다. 그 덕분에 오랫동안 활동할 수 있었던 것 같아요.

Q 폴리매스 활동이 어떤 도움이 됐나요?

전에는 문제를 풀기만 했었는데, 문제를 내다보니 출제자의 관점에서 수학 문제를 바라볼 수 있게 됐어요. 다른 사람들이 쓴 풀이를 읽어보면서 제가 몰랐던 개념이나 공식을 배우고, 문제의 오류를 발견하기도 해요. 혼자서 공부할 때는 ‘이런 문제는 이렇게 풀어야 한다’는 고정관념에서 벗어나지 못했는데, 한 문제에도 다양한 풀이법이 있다는 것을 깨닫게 됐어요!

Q 장래 희망은 무엇인가요? 왜 그런 꿈을 꾸게 됐는지 함께 알려주세요~.

저는 데니스 홍 박사님처럼 인류를 돕는 로봇을 만드는 로봇공학자가 되고 싶습니다. 로봇은 재난 현장처럼 실제 사람이 들어가기에는 위험한 곳에서 사람의 목숨을 구할 수 있잖아요. 그리고 매년 로봇들이 축구 실력을 겨루는 로보컵이 열리는 데요, 2050년에는 로보컵 대회 우승팀이 월드컵 챔피언과 겨루는 것을 목표로 하고 있다고 해요. 2050년에 로봇과 인간이 축구하는 모습을 꼭 보고 싶어요!