d라이브러리

피보나치의 모든 것!
피보나치 수

두 수가 주어졌을 때 두 수를 더한 수가 두 수의 다음 수가 되도록 배열된 경우를 피보나치 수열이라 한다. 피보나치 수는 피보나치 수열에 나오는 수를 일컫는다. 피보나치는 이탈리아의 수학자 레오나르도 피보나치(1170~1250)의 이름을 따서 붙인 명칭이다. 예를 들어 다음 수열은 피보나치 수열이다. 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…수학에서는 여기에 1을 더 첨가해 피보나치 수열을 1, 1, 2, 3, 5, 8, 13,… 과 같이 생각하기도 한다.

피보나치 정사각형, 정육면체, 직육면체

한 변의 길이가 피보나치 수인 정사각형을 피보나치 정사각형이라 한다. 이때 정사각형의 넓이는 각각 1, 1, 4, 9, 25, 64, 169,… 이다. 또 한 모서리의 길이가 피보나치 수인 정육면체를 피보나치 정육면체라 한다. 이때 정육면체의 부피는 각각 1, 1, 8, 27, 125, 512, 2197,… 이다.
 한편 각 모서리의 길이가 피보나치 수인 직육면체는 피보나치 직육면체라 한다. 이때 직육면체의 부피는 각각 1×1×2, 1×2×3, 2×3×5, 3×5×8,… 이다.

피보나치 나선

피보나치 정사각형을 만들어 그림 ❶과 같이 이어 붙이자. 컴퍼스를 이용해 그림 ❷와 같이 사분원(원의 4분의 1에 해당하는 부채꼴)을 그리면 사분원의 둘레는 하나의 나선이 된다. 이 나선을 피보나치 나선이라고 한다.
 

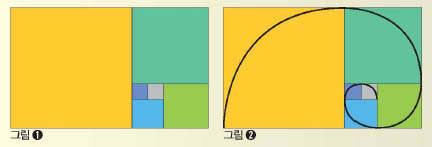
피보나치 수열에서 이웃한 두 수에 대해 큰 수를 작은 수로 나누어 비율을 구하면 두 수가 커질수록 그 값은 황금비(약 1.618)에 가까워진다. 그래서 피보나치 나선을 ‘황금나선’이라 부르기도 한다.

피보나치 직사각형과 직육면체

피보나치 직사각형

피보나치 정사각형 여러 개를 연결하면 피보나치 직사각형을 만들 수 있다. 그리고 이들의 면적 사이엔 다음과 같은 등식이 성립한다.

1²+1²=1×2
1²+1²+2²=2×3
1²+1²+2²+3²=3×5
1²+1²+2²+3²+5²=5×8
1²+1²+2²+3²+5²+8²=8×13
…

주어진 그림의 피보나치 직사각형 면적은 1²+1²+2²+3²+5²+8²=8×13이다. 이와 같이 피보나치 정사각형을 이용해 피보나치 직사각형을 만들 수 있다.

피보나치 정사각형과 직육면체로 만든 직육면체

수학실험실에서 피보나치 정육면체와 피보나치 직육면체를 결합해 만든 직육면체의 부피를 직접 구해 확인해 보자.
❶ 한 모서리의 길이가 1인 정육면체 2개와 모서리의 길이가 (1, 1, 2)인 직육면체, 그리고 한 모서리의 길이가 2인 정육면체를 결합하면 모서리의 길이가 (2, 2, 3)인 직육면체가 된다. 이것을 수식으로 나타내면 1³+1³+2³+(1×1×2)=2×2×3이다.
❷ 또 ①에서 만든 직육면체에 한 모서리의 길이가 3인 정육면체와 모서리의 길이가 (1, 2, 3)인 직육면체를 결합하면 모서리의 길이가 (3, 3, 5)인 직육면체가 된다. 이것을 수식으로 나타내면 1³+1³+2³+3³+(1×1×2)+(1×2×3)=3×3×5이다.
❸ 같은 방법으로 ②에서 만든 직육면체에 한 모서리의 길이가 5인 정육면체와 모서리의 길이가 (2, 3, 5)인 직육면체를 결합하면 모서리의 길이가 (5, 5, 8)인 직육면체가 된다. 식으로 나타내면 1³+1³+2³+3⁵+5³+(1×1×2)+(1×2×3)+(2×3×5)=5×5×8이다.
 이처럼 피보나치 정육면체와 피보나치 직육면체를 이용해 커다란 직육면체를 만들 수 있다.