d라이브러리

여러분! 제가 오랜 유학 생활을 마치고 한국에 돌아왔습니다. 3월부터 서울대학교에서 수리과학분야 박사후연구원으로 지내게 됐어요. 제가 좋아하는 파이데이를 한국에서 보낼 수 있어서 더 기쁘네요. 제가 연구하는 군론도 파이데이에 빠질 수 없겠죠? 대칭을 연구하는 군론과 원의 관계를 함께 알아봅시다.

수학로그를 꾸준히 읽은 독자라면, 제가 연구하는 수학 분야가 군론이라는 걸 기억할 겁니다. 군론이 생소한 분을 위해 간단히 소개하면 군론은 대칭을 수학적으로 연구하는 분야예요.

수학을 공부하다 보면 대칭이란 단어를 많이 접하게 됩니다, 학교에서는 주로 도형의 회전 대칭과 반사 대칭을 배우죠. 회전 대칭은 하나의 평면 도형을 일정 각도만큼 회전할 때 처음의 도형과 완전히 겹쳐지는 것을 말합니다. 정삼각형은 시계방향으로 120°, 240°, 360°를 회전시키면 처음과 똑같은 모양이 나옵니다. 한편, 반사 대칭은 한 축을 기준으로 반사하면 같은 모양이 나오는 것을 말합니다. 정삼각형의 경우, 꼭짓점을 지나는 수직선을 축으로 반사하면 원래 모양과 똑같은 정삼각형이 되죠. 

정삼각형을 대칭적이라고 하는 이유는 이렇게 6가지 대칭이동이 가능하기 때문입니다. 이 6가지 대칭이동을 아무리 복잡하게 섞어도 나오는 모양의 종류가 6가지 중 하나인데, 이렇게 가능한 대칭이동을 모아놓은 집합을 ‘군’이라고 합니다. 즉, 군론은 대칭의 규칙을 수학적으로 연구하는 학문입니다. 

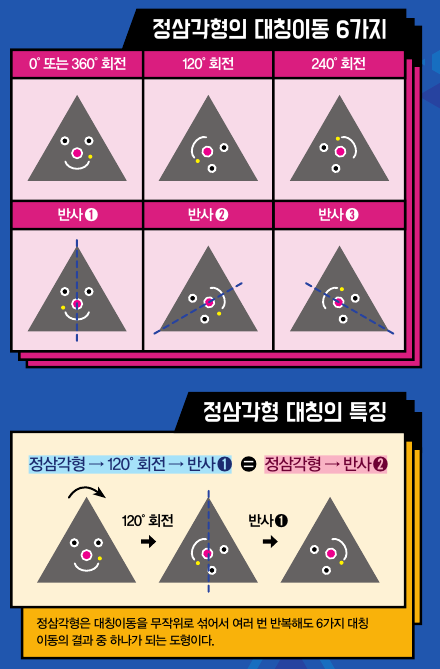
원, 무한한 대칭

수학을 좋아하는 사람들이 매년 3월 14일 파이데이를 기념하는 이유는 3.14159265…로 무한히 이어지는 파이, 즉 원주율이 수학에서 아주 특별한 수이기 때문입니다. 수학 분야가 아니어도 원주율과 원은 과거부터 아주 특별했습니다. 동서고금을 막론하고 여러 문명에서 원은 신의 상징, 혹은 완벽의 상징으로 여겨왔습니다. 어느 한쪽으로 기울지 않고 완전한 균형을 이루고 있기 때문이죠. 
군론에서도 원은 아주 특별합니다. 대칭의 관점에서 보면 원은 완벽히 대칭적인 도형이기 때문입니다. 앞에서 본 정삼각형의 대칭이동은 6개였습니다. 이를 일반화하면 모든 정n각형은 2n개의 대칭이동을 갖고 있습니다. 이러한 성질을 군론에서는 ‘정n각형 이면군’이라 부르며, 주로 D2n으로 표현합니다. 

그럼 원의 대칭은 몇 개일까요? 잠시 생각해 보면 원은 어떻게 회전하거나 반사해도 모양이 처음 모양에서 변하지 않는다는 걸 알 수 있습니다. 원은 한마디로 무한한 대칭을 갖는, 완전한 균형 그 자체인 셈이죠.

원의 회전 대칭과 단위원군

2차원 도형의 두 가지 대칭인 회전 대칭과 반사 대칭 중에서 회전 대칭만을 모은 집합을 생각해 볼까요? 앞서 확인했듯이 정삼각형은 3개의 회전 대칭을 가지고 있습니다. 회전 대칭의 특징은 각도를 더하면 대칭이동 사이의 상호작용을 이해할 수 있다는 점입니다. 예를 들어 정삼각형을 시계방향으로 먼저 120° 돌리고 그 후 다시 120° 돌리는 것은 한 번에 240°를 돌리는 것과 같은 대칭이동입니다. 비슷하게 먼저 240°를 돌리고, 그 후 다시 240°를 돌리는 것은 한 번에 120°를 돌리는 것과 같은 대칭이동입니다. 240°+240°=480°지만 360°는 이미 한 바퀴를 돌아버린 셈이니 120°를 돌린 것과 같아지는 셈이죠. 

회전 대칭은 대칭이동의 순서가 중요하지 않다는 특성이 있습니다. 240°를 먼저 돌리고 120°를 돌리거나, 120°를 먼저 돌리고 240°를 돌리거나 똑같이 한 바퀴를 돌리는 대칭이동이죠.

이제 원의 회전 대칭을 생각해볼까요? 완벽한 대칭의 상징인 원답게, 원은 무한한 회전 대칭을 갖고 있습니다. 어떤 각도로 돌려도 회전 대칭인 모양이 나오기 때문이죠. 원의 회전 대칭을 모은 군을 ‘단위원군(Circle Group)’이라고 부릅니다.

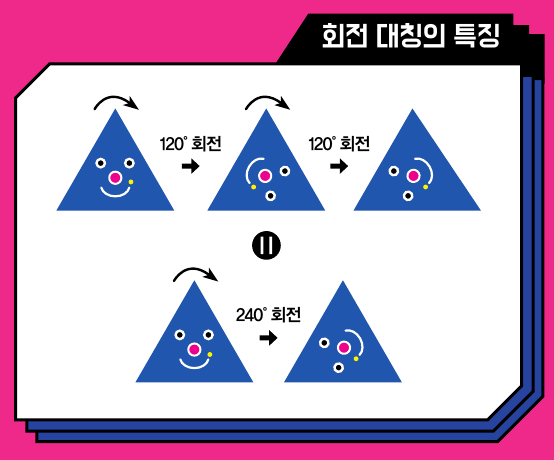
다양한 곳에서 나타나는 단위원군

그렇다면 수학에서 단위원군은 어떤 의미가 있을까요? 도형의 관점에서만 바라보면 원의 무한한 회전 대칭이 수학에서 왜 중요한지 상상이 안될 수 있습니다. 하지만 단위원군은 여러 수학 분야에서 다양한 형태로 예상치 못한 곳에서 나타납니다. 마치 원주율이 전혀 관련 없어 보이는 오일러 항등식(e^iπ+1=0)에서 나타나는 것처럼요.

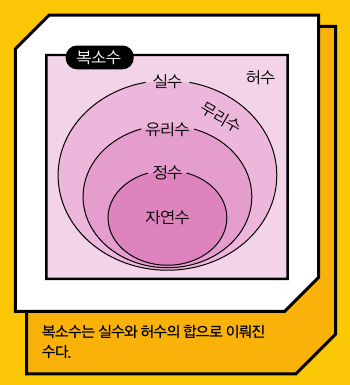
정n각형 이면군을 D_2n으로 표현하는 것처럼, 원의 단위원군은 T로 표현합니다. 수학적으로 이 단위원군의 정의는 ‘절댓값이 1인 복소수의 집합’입니다. 실수와 허수에서 나오는 그 복소수가 맞습니다. 복소수는 수를 확장한 개념으로, 복소수 z는 실수(a)에 허수(bi)를 더해 z=a+bi꼴로 나타냅니다. 따라서 실수는 복소수라는 집합에서 b가 0인 부분집합이라고 할 수 있습니다. 

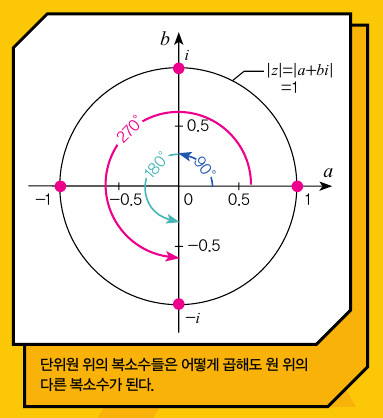
대체 원의 회전 대칭과 복소수가 무슨 관련이 있는지 궁금해할 독자들이 많을 텐데요, 아주 간략히 설명하면 좌표평면에 절댓값이 1인 복소수들을 그리면 반지름이 1인 단위원이 나옵니다. 

단위원군이라는 이름도 여기서 유래했죠. 두 복소수 x, y가 있을 때, 이 둘의 곱인 xy의 절댓값은 x의 절댓값과 y의 절댓값의 곱과 같다는, 즉 |xy|=|x||y|라는 특성에 따라 절댓값이 1인 복소수끼리는 어떻게 곱해도 절댓값이 1인 복소수가 됩니다. 이제 공통점이 보이나요? 원의 회전 대칭을 어떻게 섞어도 원의 회전 대칭 모양이 나오듯, 단위원에 있는 복소수를 어떻게 곱하든 단위원에 있는 다른 복소수가 되는 것이죠.

예를 들어 i×(-1)=-i는 90° 회전과 180° 회전을 더한 것이 270° 회전과 같다는 의미입니다. 단위원군에서의 곱셈은 각도의 덧셈으로 볼 수 있죠. 이렇듯 절댓값이 1인 복소수들의 곱셈은 원의 대칭이동에서 각도를 더하는 것에 대응할 수 있습니다.

원의 회전 대칭의 중요성은 여기서 끝이 아닙니다. 단위원군 T는 수학에서 흔히 다음과 같이 다양한 형태로 표현합니다:

이 군들은 수학의 여러 분야에서 중요한 의미가 있으며, 특히 SO(2,ℝ)이라는 특수직교군은 물리학, 특히 원자의 세계가 어떻게 작동하는지 설명하는 양자역학에서 핵심적 역할을 합니다. 원이 수학에서 특별한 존재인 만큼 원의 대칭으로 이뤄진 군 역시 수학에서 다양한 형태로 쓰이는 것을 아시겠죠? 

파이데이 행사에 참여해 본 독자들도 원의 대칭과 군론의 관계를 들어본 적은 별로 없었을 겁니다, 이번 파이데이에는 원의 완벽한 대칭을 보며 군론에도 관심을 가져보면 어떨까요?