d라이브러리

19세기 프랑스의 수학자 앙리 푸앵카레가 제시한 ‘푸앵카레 추측’은 ‘끊긴 부분이 없이 닫힌 3차원 다양체는 구면과 위상동형이다’라는 내용입니다. 100여 년 묵은 이 난제는 2002년 러시아 수학자 그리고리 페렐만이 증명하면서 해결됐습니다. 하지만 푸앵카레 추측을 4차원으로 확장한 ‘매끄러운 4차원 푸앵카레 추측’은 풀리지 않았죠.
그런데 20여 년만인 2020년 11월 21일, 매끄러운 4차원 푸앵카레 추측을 풀  실마리가 될 수 있는 난제인 ‘해밀턴-티엔 추측’이 해결됐다고 중국과학원 연구팀이 발표했습니다. 이런 재미있는 수학 소식을 그냥 넘어갈 순 없죠! 함께 어떤 내용인지 알아볼까요?

20년 만에 찾은 난제의 실마리, 해밀턴-티엔 추측 파헤치기!

STEP1 난제의 기원을 찾아서~

1982년 리처드 해밀턴 미국 컬럼비아대학교 수학과 교수는 열이 어떻게 확산하는지 나타내는 방정식을 기하학에 도입했어요. 공간에서 열의 분포가 시간에 따라 바뀌는 것과 비슷하게 물체의 기하학적인 형태가 시간에 따라 변할 거라고 생각한 거죠. 이를 ‘리치 흐름’이라고 해요. 리치 흐름에 따르면 울퉁불퉁한 돌도 볼록한 부분은 점차 줄어들고 홀쭉한 부분은 점차 부풀며 결국 하나의 구 모양이 돼요. 열이 확산하듯이 물건을 변형시키면 물건 위에서의 길이나 각도 같은 기하학적 성질은 변해도 위상수학적 성질은 변하지 않습니다. 여기서 위상수학적 성질이란 구멍은 몇 개인지, 계속해서 뻗어 나가는 부분이 있는지 등 도형의 본질적인 성질을 말해요. 그리고 이 도형의 본질을 연구하는 분야가 위상수학입니다. 위상수학에서는 구멍이 하나인 도넛과 머그컵은 본질적으로 같은 물체라고 보고 이를 위상적으로 같다는 의미인 ‘위상동형’이라고 불러요. 원과 삼각형, 사각형 역시 모두 같은 위상동형인데요, 뾰족한 부분을 잘 펴면 원과 같은 모양이 되기 때문입니다.

위상수학을 연구하는 수학자들은 다양한 도형의 본질을 파악하기 위해 리치 흐름을 사용해요. 우리가 보기엔 제각각 다른 도형들도 리치 흐름에 따르면 가장 단순한 모습으로 변하거든요. 1982년 미국 수학자 윌리엄 서스턴은 모든 종류의 3차원 다양체를 리치 흐름으로 단순화시켰을 때 8개의 모양이 나온다는 것을 알아냈습니다. 그리고 2002년 그리고리 페렐만이 8개의 모양을 리치 흐름으로 단순화할 때 생기는 특이점을 잘라서 붙이는 새로운 ‘수술법(surgery)’을 선보이며 구면과 위상적으로 같아지는 것은 결국 구면 단 하나라는 것을 증명해냈죠. 특이점이란 미분이 불가능한, 매끄럽지 않고 뾰족한 부분을 말해요. 3차원 다양체에 대한 푸앵카레 추측이 해결되면서 우주가 끊긴 부분이 없는 닫힌 3차원 다양체라면 구면과 위상동형이라는 것을 알아낸 거죠.

수학자들은 리치 흐름을 사용해 다양한 차원에 존재할 수 있는 가장 단순화된 형태인 ‘궁극의 모양’을 알아보려 했습니다. 각 차원에 존재하는 다양체 중에 끊어지거나 뾰족한 부분이 없는 매끄러운 다양체가 있는지, 있다면 어떤 모양인지 확인하고 싶었던 거죠. 그런데 0~3차원과 5차원 이상의 다양체는 쉽게 밝혀진 반면 4차원 다양체는 유독 해결되지 않았어요. 그렇게 매끄러운 4차원 푸앵카레 추측이 탄생했습니다.

수학자들은 4차원 다양체의 궁극의 모양을 알아내기 위해 4차원 다양체와 비슷한 성질을 가진 다른 차원의 다양체를 연구했는데, 그중 하나가 ‘켈러 다양체’에요. 이 켈러 다양체를 연구하는 티엔 강 중국 베이징대학교 교수가 1997년 자신의 논문에서 ‘켈러 다양체를 리치 흐름에 따라 변화시키면 특이점의 차원은 켈러 다양체의 차원보다 4 이상 작을 것이다’라는 추측을 발표했죠. 이 추측은 리치 흐름을 만든 리처드 해밀턴과 티엔 강의 이름을 따 ‘해밀턴-티엔 추측’이라고 부릅니다.

STEP2 4차원 자매품, 켈러 다양체

다양체, 특이점도 어려운데, ‘켈러 다양체’는 또 뭐냐고요? 당황하지 말고 추측에 등장한 용어부터 하나씩 알아볼게요. 먼저 켈러 다양체는 특정한 성질을 가진 2차원, 4차원, 6차원 같은 짝수 차원의 다양체를 말해요. 

다양체는 앞서 설명한 것처럼 도형의 일부가 선, 면, 공간처럼 거리를 잴 수 있는 유클리드 공간에 있는 성질을 갖는 것을 말합니다. 작은 난쟁이들이 왼쪽 그림처럼 클라인 병 위에서 이동한다고 상상해 봅시다. 난쟁이들은 x축과 y축으로 이동할 수 있습니다. 다시 말해 난쟁이들이 있는 클라인 병은 2차원 평면으로 이뤄진 2차원 다양체죠. 그렇다면 우주는 몇 차원 다양체일까요? 우주에서는 하나의 축이 더 생겨 z축 방향으로도 이동할 수 있으니 총 3개의 방향으로 움직일 수 있습니다. 그렇기 때문에 우주는 3차원 다양체인 겁니다. 4차원 다양체는 여기에 하나의 축을 더해 4가지 방향으로 이동할 수 있고 n차원 다양체에서는 n가지 방향으로 이동할 수 있겠죠.

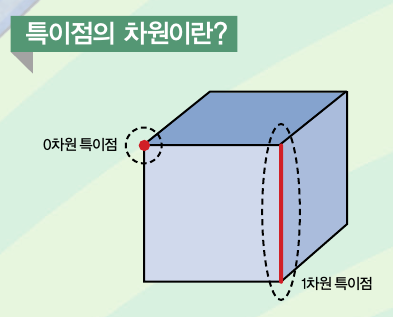
또 다른 어려운 말은 ‘특이점의 차원’이라는 말인데요. 특이점 역시 차원이 존재합니다. 어떤 다양체를 리치 흐름에 따라 변화시킨 모습이 정육면체의 모습이라면 꼭지점은 0차원, 모서리는 1차원 특이점입니다. 

STEP3 해밀턴-티엔 추측 이해하기

이 내용을 종합해 해밀턴-티엔 추측을 이해해보면 n차원 켈러 다양체를 리치 흐름에 따라 변화시키면 특이점의 차원은 (n-4)차원 이하일 것이라는 말이죠. 예를 들어 봅시다. 6차원의 켈러 다양체를 리치 흐름에 따라 변화시키면 미분 불가능한 뾰족한 특이점들은 0차원, 1차원, 2차원(6-4=2) 중에 있다는 의미입니다. 그렇다면 4차원 켈러 다양체에 리치 흐름을 적용해 특이점을 얻는다면 어떨까요? 그 특이점은 오직 한 점으로 모이는 0차원(4-4=0)뿐으로 1~3차원 특이점은 없다는 뜻입니다. 4차원 다양체가 궁극적으로 어떤 모양일지 감도 잡지 못했던 상황에서 이 추측이 해결된다면, 일부 4차원 다양체의 궁극적인 모양과 특이점에 대한 궁금증이 해결될 수 있는 거죠.

2014년 5월 중국과학원 기하물리학연구소의 설립자인 씨우시옹 천과 중국과학원 수학과 빙 광 교수는 해밀턴-티엔 추측을 증명하는 120쪽이 넘는 논문을 발표했습니다. 두 사람은 5년에 걸쳐 n차원 켈러 다양체를 리치 흐름에 따라 변화시키면 기껏해야 (n-4)이하 차원의 특이점을 갖는 형태로 수렴한다는 것을 증명해냈습니다. 논문은 무려 6년의 검증을 거쳐 수학계의 인정을 받고 2020년 11월 ‘미분기하학저널’에 게재됐어요.

STEP4 해밀턴-티엔 추측의 의미

그렇다면 해밀턴-티엔 추측을 해결하는 것은 수학계에 어떤 의미일까요? 최경수 고등과학원 교수님은 “수학 연구는 크게 두 가지 방향이 있는데, 이론을 발전시키는 것과 추측을 해결하는 것”이라며 “해밀턴-티엔 추측을 해결한 것은 두 가지를 모두 만족하는 중요한 사건”이라고 말했어요. 해밀턴-티엔 추측은 기하학 중에서도 리치 흐름을 사용하는 분야인 ‘기하학 흐름’의 최고 난제였어요.

최고 난제가 해결된만큼 기하학 흐름 이론을 발전시켰죠. 그리고 미지의 4차원 다양체의 궁극적인 모양에 대한 단서를 제시함으로써 기하학 분야의 역사적 난제인 매끄러운 4차원 푸앵카레 추측에 대한 새로운 단서 역시 제공했다고 할 수 있죠. 매끄러운 4차원 다양체가 2개 이상 존재하는 것을 밝힌 공로로 1986년 필즈상을 수상한 사이먼 도널드슨 역시 “기하학적 연구의 주요 돌파구이며 다양한 관련 연구를 이끌 것”이라고 말했답니다.
 

조금 어렵긴 하지만 알면 알수록 재미있는 위상수학의 세계! 여러분이 수학자가 돼 아직 완벽히 풀리지 않은 4차원 다양체의 비밀을 파헤쳐보는 것은 어떨까요?