d라이브러리

코로나19로 중요하게 떠오른 사회적 거리두기 문제는 물론 펭귄이 추위를 견디는 가장 효과적인 전략, 먼 거리의 우주 통신을 할 때 생기는 왜곡은 모두 ‘이 수학 문제’로 해결할 수 있습니다. 그 해결법은 무엇일지, 충분히 생각해본 뒤에 답을 확인하세요!

만능 해결사 ‘채우기 문제’란?

채우기 문제는 평면에서 원을 겹치지 않게 가장 많이 배열하거나 공간에서 구를 가장 밀집하게 배치하는 방법을 찾는 문제입니다. 약 400년 전 독일 천문학자 요하네스 케플러가 처음 제시했죠. 2차원 문제는 1940년대 헝가리의 수학자 라슬로 페예시 토트가, 3차원 문제는 미국 수학자 토마스 헤일스가 1998년에 해결했습니다. 대체 어떤 문제인지 제대로 알아봅시다.

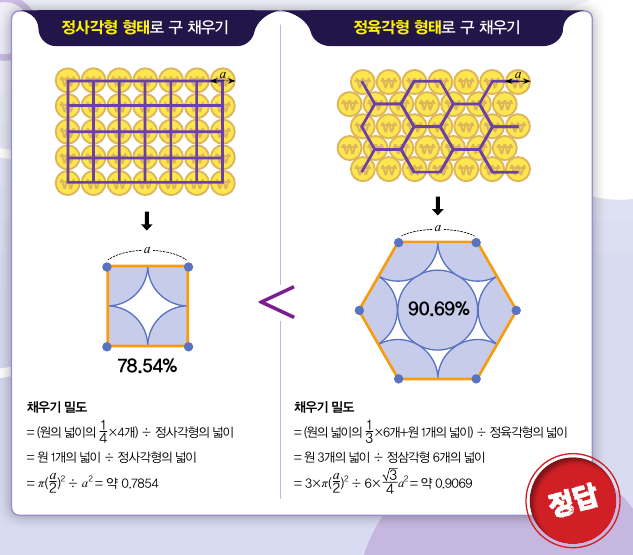
2차원 채우기 문제의 정답은?

평면에 원을 조밀하게 배치하는 방법은 크게 두 가지예요. 하나는 정사각형 격자의 꼭짓점에 원의 중심을 배치하는 것, 다른 하나는 정육각형 격자의 꼭짓점에 원의 중심을 배치하는 것이죠. 정사각형과 정육각형 모두 각 도형을 연달아 이어붙이면 평면을 빈틈없이 메울 수 있기 때문에 그 구조로 원을 배치하고, 버려지는 공간이 얼마나 되는지 따져보겠습니다. 원의 지름과 정사각형, 정육각형의 한 변의 길이가 a라고 할 때 원이 덮는 넓이의 비율을 구해봅시다.

3차원 이상의 공간에선?

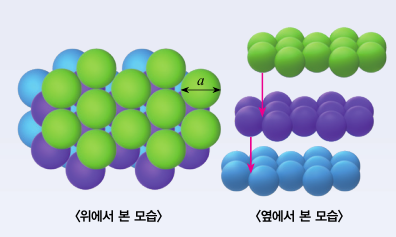
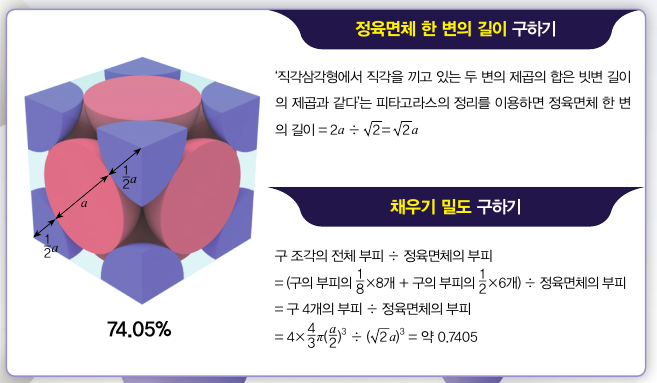
3차원 공간의 단면은 2차원이기 때문에, 평면에서 원을 정육각형 형태로 배치했던 것처럼 3차원에서도 상하좌우 어느 방향에서 봐도 정육각형 형태를 이루도록 빽빽하게 쌓아야 합니다. 이렇게 쌓은 구조를 ‘면심 입방 구조’라고 합니다. 밀도를 구하기 위해서는 한 면의 대각선 길이가 구 지름의 2배인 정육면체 형태로 일부를 잘라 구할 수 있습니다. 아래의 두 단계를 거쳐 채우기 밀도를 구해볼까요?

수학동아 독자, 수학자의 결과를 뒤집다?!

채우기 문제의 활약이 대단하죠? 그런데 이 문제를 활용해 재밌는 연구를 한 수학동아 독자가 있습니다. 연구 결과가 수학자의 결과와 상반돼 더욱 의미있다고 하는데요, 어떤 이유에서일까요?

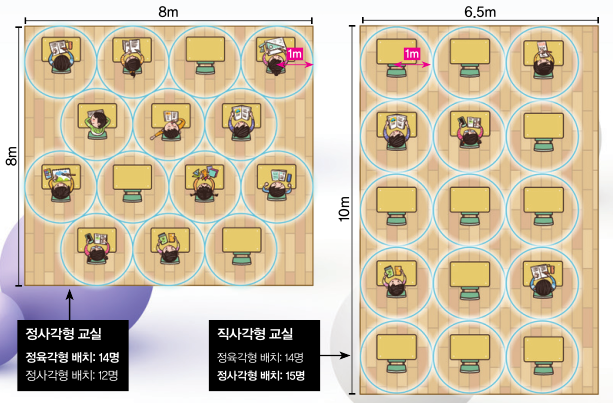
강민지 봉림중학교 3학년 학생은 코로나19 확산을 막기 위해 학생들이 교실에서 2m 간격을 유지하면서 수업을 들을 수 있을지 걱정됐습니다. 그래서 서로 일정 거리를 두는 ‘2차원 채우기 문제’를 떠올리고 연구에 돌입했습니다.

먼저 교실에서 교탁과 칠판 등을 둘 공간을 제외한 학생들이 앉을 수 있는 공간을 정사각형일 때와 직사각형일 때로 나눴습니다. 그리고 한 변의 길이가 8m인 정사각형과 가로 6.5m, 세로 10m인 직사각형을 모눈종이에 그리고 그 위에 반지름이 1m인 원을 서로 접하게 그린 뒤 그 개수를 셌습니다.

그 결과 정사각형 교실에서는 원을 정육각형 배치로 했을 때 14개로 가장 많았지만, 직사각형 교실에서는 정사각형 배치가 15개로 정육각형 배치보다 1개 더 많았습니다. 정육각형 배치가 항상 효율적이라고 생각할 수 있지만, 그 생각을 뒤엎은 결과죠.

이 연구를 본 김종락 서강대학교 수학과 교수는 “수학자의 연구는 평면 전체를 채우는 것인데, 교실 상황에 적용하기 위해 공간을 직사각형 등 특별한 모양으로 가정한 것이 다른 해법이 나온 이유”라고 분석했습니다. 강민지 학생 역시 다른 결과가 나온 이유를 ‘평면의 성질’로 봤죠. 가로세로의 길이가 같은 정사각형은 무한평면과 같기 때문에 2차원에서의 채우기 방법인 정육각형 배치가 가장 높은 효율을 보였지만, 직사각형은 가로세로의 비율이 다른 유한 평면이라 비율이 일정한 원을 정육각형 격자로 쌓으면 원의 일부가 잘려 낮은 밀도를 보였다고 분석했습니다. 따라서 교실을 다양한 크기로 바꿀 수 있는 가벽을 설치한다면 사회적 거리두기를 유지하면서도 높은 효율로 공간을 활용할 수 있을 것이라 예상했습니다.

교실에서의 사회적 거리두기와 펭귄, 우주 통신을 아우르는 채우기 문제의 위력을 보셨나요? 여러분도 주변에서 수학으로 해결할 만한 문제를 찾아 제보해주세요! 제보가 모이면 정답 누설 수학 퀴즈쇼는 돌아옵니다!