d라이브러리

가장 논란의 여지가 없는 학문, 누가 풀어도 바뀌지 않는 절대 진리. 아마 수학에 대해 많은 사람들이 가진 인식일 겁니다. 실제로 수학은 그 논리성과 이성에 충실하며 우리 삶에 많은 도움을 주었습니다. 그런데 그런 수학이 거짓말을 하다니요? 심지어 학생들이 믿어 의심치 않는 수학 교과서가? 당최 이게 무슨 말인지, 진실은 무엇인지 청문회에서 확인해보겠습니다.

보편적으로 생각하는 수학의 특징이라고 하면 어떤 것이 있을까요? 

그 외에도 여러 가지가 있겠지만 모두 ‘확실성’에 기초하고 있다는 공통점이 있을 겁니다. 그런데 의외로 수학 교과서의 수학이 거짓말을 꽤 한다는 사실, 알고 계셨나요? 우리가 믿어 의심치 않던 수학 교과서는 다양한 방식으로 우리를 속여 왔습니다. 
세상에서 거짓말과는 가장 무관해 보이는 수학이 어떻게 거짓일 수 있으며 수학 교과서가 왜 우리를 속이고 있는지 파헤치다 보면 그동안 몰랐던 수학의 새로운 면모를 만날 수 있을 겁니다. 무심코 지나왔던 수학 교과서가 어떤 방법으로 우리를 1과 2도 구분하지 못하는 단계에서 미·적분

까지 가능하도록 이끌었는지, 또 충분히 알고 있다고 생각했던 부분을 벗어나 어떤 세계를 감추고 있었는지 청문회를 통해 알아보겠습니다. 

팩트체크V 수 체계

이 증언은 실제로 인터넷상에서 네티즌들에게 수천 회 공유되면서 공감을 얻었던 내용입니다. 수학 교과서가 전 학습 단계에서 배운 내용을 계속 번복하고 있다는 거지요. 맞습니다. 교과서는 수를 효과적으로 설명하기 위해 의도된 번복을 거듭하고 있습니다!

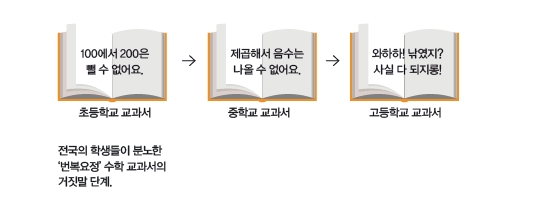
수의 종류에는 여러 가지가 있습니다. 자연수, 정수, 무리수, 허수 등이지요. 국내 교육과정에서는 초등학교 때까지는 자연수를 주로 배웁니다. 중학생이 되면 유리수, 무리수 등을 포함한 실수를 배우며, 고등학교에 이르면 복소수까지 배웁니다. 그럼 처음부터 그냥 다 알려주고 계산하면 되지 왜 굳이 번거로운 과정을 거치는 걸까요?

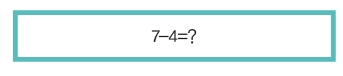
위 식을 살펴봅시다. 초등학생이 보든 중학생이 보든 답은 ‘3’이란 걸 금방 알 수 있습니다. 그런데 그 대답을 하기까지의 과정은 사뭇 다릅니다. 초등학생과 중학생은 수를 다루고 인식하는 방법 자체가 다르거든요. 

초등학교 경험 vs 중학교 논리

초등학교 수학은 ‘경험’을 바탕으로 연산을 설명합니다. 예를 들어 ‘냉장고에 푸딩 7개가 있었는데 태형이가 4개 먹었다면 남은 푸딩은 몇 개일까요?’라는 식이죠. 그래서 분수, 소수 등의 유리수도 ‘모눈종이 9칸 중에서 2칸을 색칠한 숫자’, ‘막대기를 7등분하고 3칸을 칠한 숫자’로 표현합니다. 실제 의미의 ‘유리수’가 아닌 자연수를 도구로 실험해서 만들어낸 수가 되는 거지요.  
반면 중학교 수학은 본격적으로 수를 양이 아닌 수 자체로 배우기 시작합니다. 중학교에 들어가면 가장 먼저 배우는 ‘음수’는 초등학교 수학과 중학교 수학을 가르는 대표적인 사례죠. 그림을 그려서 수학을 배우던 초등학생에게 ‘-3’을 표현해보라고 하면 아주 곤란해할 겁니다. 이 단계에서부터 연산은 눈에 보이는 사물의 조합을 넘어 수들의 관계를 통해 정의되는 논리적인 규칙이 됩니다. 음수 -3은 ‘사과 1개에서 4개를 빼고 남은 양’이 아니라 ‘양수 3을 더했을 때 0이 되게 하는 수’로 정의되고, 무리수 는 ‘제곱해서 2가 되는 수’로 정의되는 식이죠. 
경험으로 수학을 배우는 초등학교, 경험을 넘어선 논리로 수학을 배우는 중학교 이후 교과서에서 수를 다르게 다루는 이유를 아시겠죠?  이처럼 수학 교과서는 단순히 어렵고 쉬운 문제의 차이가 아닌 생각하는 방식의 차이를 담고 있기 때문에 단계에 따라 자연스럽게 달라진 겁니다.    

팩트체크V. 유클리드 기하학과 비유클리드 기하학

수학 교과과정 중 가장 많은 거짓말이 들어있는 분야는 단연 ‘기하학’이라고 할 수 있습니다. 실제 세상에서는 삼각형의 내각의 합은 180°가 아니며, 평행한 두 직선은 만날 수도 있고 만나지 않을 수도 있고, 두 점 사이 최단 거리는 직선이 아닙니다. 심지어 선 2개로 ‘이각형’도 만들 수 있죠! 
이런 초유의 거짓말 사태가 일어난 이유는 우리가 초등학교, 중학교, 고등학교를 거쳐 교육과정에서 배우는 기하학은 ‘유클리드 기하학’이기 때문입니다. 유클리드 기하학은 고대 그리스 수학자인 에우클레이데스(유클리드)가 정립한 수학 분야로, 최초로 ‘기하학’이라는 분야를 체계적으로 정리한 학문입니다. 그리고 무려 2000년 동안 널리 쓰이며 ‘절대 진리’로 여겨졌습니다. 19세기에 이르러 다른 관점이 제시되기 전까지는 말이죠. 

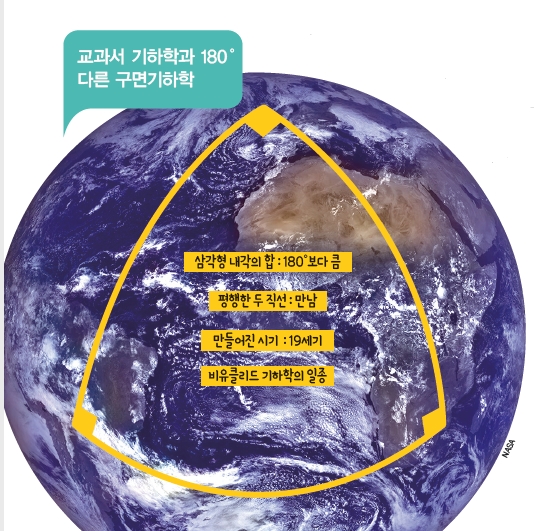
이탈리아 수학자 지오바니 사케리를 시작으로 많은 수학자가 연구를 거듭한 끝에 유클리드 기하학을 이루는 5번째 공리인 ‘평행선 공리’를 거짓이라고 가정해도 그 기하학에 모순이 없다는 것을 밝혔습니다. 오히려 평행선 공리를 부정하자 기존의 기하학으로는 설명할 수 없는 새로운 기하학이 탄생했습니다. 이처럼 유클리드 공간을 벗어난 여러 기하학을 통틀어 ‘비유클리드 기하학’이라고 부릅니다. 비유클리드 기하학은 교과서에서 배운 내용과 많이 다르지만 실제 세계를 잘 설명하죠.
비유클리드 기하학을 배우려면 유클리드 기하학을 먼저 이해해야 하고, 유클리드 공간에서는 여전히 유클리드 기하학이 훌륭하게 성립하기 때문에 거짓말 했다고 교과서를 무작정 미워할 필요는 없습니다. 도리어 유클리드 기하학을 잘 배워서 비유클리드 기하학까지 공부하면 두 배로 유익하겠죠?  

수학 교과서의 거짓말은 발전의 단서

수학 교과서의 거짓말 단계는 인류의 수학 발전 단계를 함축해놓은 역사적 기록과도 유사합니다. 그 과정에서 때로 의도적으로 정보를 감추기도 하고 나중에 제대로 알려줄 내용을 슬쩍 다른 말로 알려주기도 합니다. 수학 교과서의 거짓말은 학생들에게 중요한 공부 장치로써 떼려야 뗄 수 없는 동반자였던 겁니다.  
반면 우리가 알아야 할 수학 교과서의 진짜 거짓말은 아직 아무도 모르게 숨어 있을 수도 있습니다. 지금 인간이 이해하는 수학도 200년 전의 유클리드 기하학처럼 절대 진리는 아닐 수도 있기 때문이죠. 정우성 포스텍 물리학과 교수는 자신의 칼럼에서 교과서의 거짓말에 대해 이렇게 말했습니다. 

현재 우리가 알고 있는 모든 법칙과 이론은 수백 년 뒤 모조리 새로운 것으로 대체될 수도 있다. 교과서의 내용을 절대 진리라고 믿고 있다면, 이것이 과연 옳은 것인지 의심하고 의문을 던지지 않는다면 더 이상의 지식의 진보와 사회의 발전은 기대하기 힘들다. 이런 호기심과 의심, 의문, 그리고 적절한 타협은 비단 수학이나 과학 뿐 아니라 삶의 전반에 필요한 덕목일지 모른다.
 
현재 절대적이라고 믿고 있는 수학도 더 발전시키다 보면 언젠가 다른 모습으로 드러날 수도 있습니다. 지금까지 그래왔던 것처럼요. 어쩌면 거짓말을 하나하나 극복해나가는 과정이야말로, 수학을 배우는 진짜 길일지도 모릅니다. 그러니 수학 교과서가 거짓말쟁이란 걸 알게 됐다면 배신감을 느끼기보다 오히려 기뻐하면서 새로운 거짓말을 찾아내 보는 건 어떨까요? 그 속에 새로운 수학이 숨어 있을 테니까요.
 
그동안 속여서 미안합니다,  하지만 저는 여러분이 쉽게 개념을 익힐 수 있도록 노력했을 뿐이에요. 앞으로도 오직 학생을 위한 거짓말만 할 것을 맹세할게요. 그리고 시험을 칠 때는 학습 단계에 맞는 답을 적으셔야 한다는 것도 잊지 마세요! 

참고자료

김용관 ‘수냐샘의 중학수학, 이렇게 바뀐다’, 모리스 클라인 
‘수학의 확실성’, 이환철·강옥기 ‘수학적 사고의 발달 메커니즘에 
기초한 교과서 분석 연구’, 정우성 ‘교과서의 거짓말’