d라이브러리

코로나19가 전세계를 강타한 현재! 각국은 대책을 세우느라 여념이 없는데요, 바이러스를 극복하기 위해 군론을 어떻게 활용하는지 함께 알아볼까요?”

인류 탄생 이래, 세균과 바이러스 등이 일으키는 무서운 전염병으로부터 인류를 보호하는 싸움은 계속됐습니다. 그리고 여러 문명이 체득한 방법들이 ‘의학’이라는 학문으로 발전했고, 과학기술이 발달하면서 지금의 ‘현대의학’이 정립되었죠.

세균은 비교적 일찍 관찰하고 정의를 내렸지만, 바이러스는 19세기 말이 돼서야 그 존재를 인지하고, 20세기 초에 구체적으로 정의합니다. 1892년 동유럽 크림반도에서 여러해살이풀인 담배가 알 수 없는 이유로 죽어갔고, 러시아의 미생물학자 드미트리 이바노프스키가 그 원인을 알아내기 위해 연구했습니다. 처음에는 이 전염병을 퍼뜨리는 세균이 있을 것이라 예상하고 현미경으로 살펴봤지만, 기존의 세균보다 너무 작아 관찰되지 않았죠. 이바노프스키는 실험을 통해 세균을 걸러내는 필터에도 걸리지 않는 작은 병원체가 있다는 사실을 알아냅니다. 

6년 뒤인 1898년 네덜란드의 미생물학자 마르티뉘스 베이예링크가 같은 방법으로 실험한 뒤 필터가 못 거르는 생물을 ‘바이러스’라고 이름 붙이죠. 나중에 알고 보니 담배를 병들게 한 원인은 ‘담배 모자이크 바이러스’였는데요, 1939년 전자 현미경이 개발되고 나서야 제대로 관찰할 수 있었고, 인류 역사상 최초로 발견한 바이러스로 기록됐습니다.

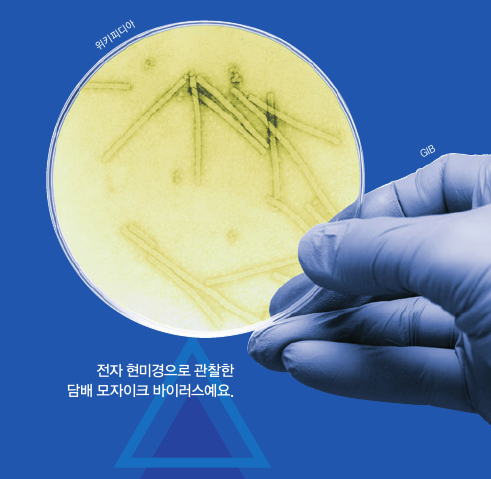
현미경 기술이 발달하면서 더욱더 많은 바이러스를 관찰해 연구하기 시작했습니다, 그런데 바이러스는 생물학적으로 굉장히 특이한 존재입니다. DNA 혹은 RNA 같은 유전 정보를 담은 핵산을 보호하는 단백질 껍질(캡시드)이 둘러싸고 있는 간단한 구조로, 스스로 번식하지 못합니다. 하지만 숙주 세포를 이용해 자신의 유전 정보를 복제하며 급속히 증식하죠. 

대칭이어야 자기 복제가 쉽다!

빠르게 자기 복제를 할 수 있는 건 바이러스의 구조가 굉장히 단순한 대칭이기 때문입니다. 복잡한 구조는 그만큼 복제하기 힘들 테니까요. 간단한 예를 들어볼까요? 종이에 같은 모양의 사각형을 10개 그려야 한다고 생각해봅시다. 임의의 사각형이 주어졌다면 이 사각형의 네 변의 길이와 변이 이루는 각도를 모두 알아야 합니다. 즉 필요한 정보가 여러 개죠. 하지만 똑같이 그려야 하는 사각형이 정사각형이라면 한 변의 길이만 알면 됩니다.

또 다른 예를 들어볼게요. 비대칭 구조의 일부가 손상됐다면 복원하기 쉽지 않습니다. 반대쪽과 구조가 달라 원래 구조가 어땠는지 정확하게 추정하기 어렵기 때문입니다. 하지만 대칭 구조의 일부가 손상됐다면 쉽게 원래 구조를 유추하고 복원할 수 있죠. 즉 바이러스의 구조가 대칭이어야 빠르게 자기를 복제할 수 있는 겁니다.

전염병과 싸우기 위해 연구자들은 이런 바이러스 껍질의 구조를 이해하고 분류하는데요, 많은 바이러스가 대칭구조이기 때문에 대칭을 수학적으로 연구하는 군론을 통해서도 연구하고 있습니다. 

1953년 DNA의 이중나선 구조를 발견한 업적으로 유명한 영국의 생물학자 프랜시스 크릭과 미국의 생물학자 제임스 왓슨은 바이러스의 유전 정보를 싸고 있는 단백질 껍질의 일부 이미지와 바이러스가 가질 수 있는 유전 정보량의 한계를 종합해 수학 모형을 만들었습니다. 바이러스 껍질를 이루는 모양은 정삼각형 아니면 정오각형 형태였습니다. 만든 수학 모형으로 분석한 결과 단백질 껍질의 기본 구조가 정이십면체와 유사할 것으로 추정했습니다. 

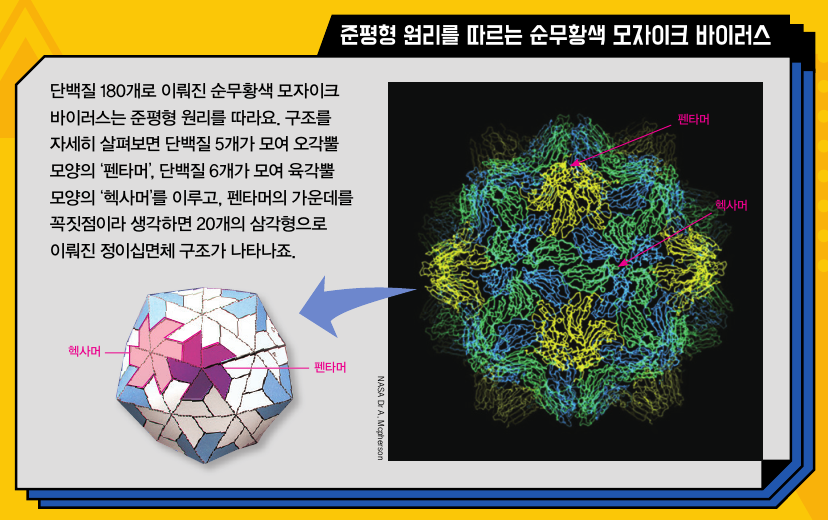
군론, 바이러스의 모양을 예측하다!

1962년 미국의 생물학자 도널드 캐스퍼와 영국의 화학자 아론 클루그는 왓슨과 크릭의 발견을 발전시켜 바이러스 단백질 껍질들이 작은 정삼각형들로 이뤄진 ‘가짜 정이십면체’ 구조를 따른다는 ‘준평형 원리’를 발표했습니다. 정삼각형 20개로 이뤄진 정이십면체가 아닌 더 작은 조각들이 모여 정이십면체와 유사한 대칭을 이룬다는 내용이었죠. 

이후 이 원리로 설명할 수 없는 다른 바이러스들도 발견됐지만 여전히 바이러스의 구조를 예측하고 분류하는 데 가장 기본적인 원리로 쓰이고 있습니다. 물론 바이러스의 구조를 예측할 수 있다고 해서 바로 치료제를 만들 수 있는 건 아닙니다. 당장 전세계를 괴롭히는 신종 코로나 바이러스 역시 이미 그 구조를 알고 있지만, 백신이나 치료제를 만들지 못하고 있거든요. 

하지만 인류는 바이러스와의 싸움에서 지금까지 이겨 왔으며, 군론은 이 전쟁의 최전선에서 바이러스의 구조를 분석하는 가장 중요한 무기로 쓰이고 있습니다. 추상적이고 이론적으로만 보였던 군론이 가장 실용적인 곳에서도 쓰이다니, 어쩌면 이게 군론의 매력이 아닐까요?