d라이브러리

2019년 11월 9일 매년 뛰어난 성과를 거둔 17세 미만 청소년에게 상을 주는 ‘트루 리틀 히어로 어워드’에서 12세 학생 치카 오필리는 새로운 7의 배수 판정법을 발견해 상을 받습니다. 그리고 치카가 발견한 방법을 ‘치카의 판정법’이라고 부르기로 했습니다. 치카의 판정법은 과연 어떤 방법일까요?

2019년 11월 9일 매년 뛰어난 성과를 거둔 17세 미만 청소년에게 상을 주는 ‘트루 리틀 히어로 어워드’에서 12세 학생 치카 오필리는 새로운 7의 배수 판정법을 발견해 상을 받습니다. 그리고 치카가 발견한 방법을 ‘치카의 판정법’이라고 부르기로 했습니다. 치카의 판정법은 과연 어떤 방법일까요?

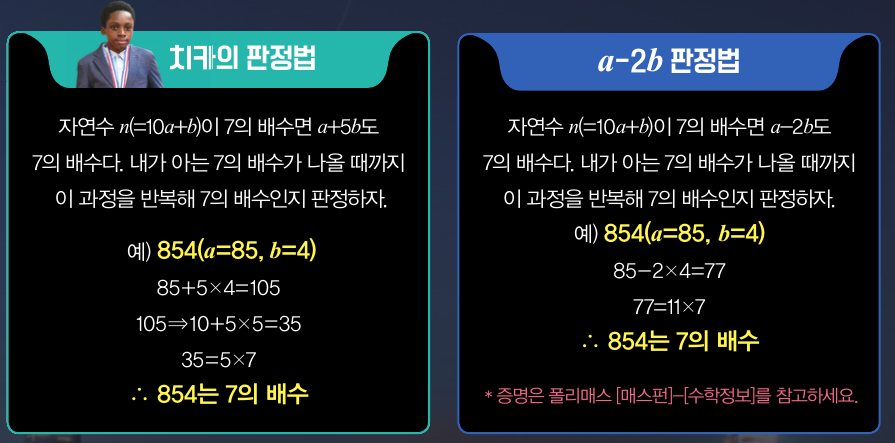
의혹1 치카의 판정법은 a-2b 판정법?

이서준 학생은 치카의 판정법이 ‘a-2b’ 판정법과 궁극적으로 같다고 주장했습니다. a-2b 판정법은 워낙 간단해서 여러 사람이 독립적으로 재발견하기도 했는데요, 10a+b 꼴인 어떤 자연수에 a-2b의 과정을 반복했을 때 나오는 값이 7의 배수이면 그 자연수는 7의 배수라는 것입니다. 1956년 영국의 수학잡지 ‘수학 가제트’에서는 스펜스의 판정법이라고 소개하기도 했죠.
이렇게 두 방식을 비교해놓으니 한쪽엔 -2를, 다른 쪽엔 5를 곱했다는 것 외에는 전체적인 계산 방식이 같아 보입니다. 하지만 -2와 5는 명백히 다른 수인데요. 이서준 학생은 왜 -2를 곱한 것과 5를 곱한 것이 같은 판정법이라고 말하는 걸까요?

의혹 2 a-2b와 a+5b가 같은 판정법?

서준 학생의 주장을 이해하기 위해선 먼저 ‘합동식’을 이해해야 합니다. 합동*이란 단어는 기하 단원에서 본 적이 있을 텐데요, 도형에서 사용하는 합동이란 개념을 정수로 옮겨와 만든 식을 합동식이라고 합니다. 합동식에서 합동은 어떤 수로 나눴을 때 나머지가 같은 수를 말합니다. 

예를 들어 15와 50은 7로 나눴을 때 나머지가 1로 같기 때문에 ‘15와 50은 7을 법으로 하는 합동’입니다. 간단히 15≡50(법 7)이라고 쓰죠. 두 수를 5로 나눴을 때도 나머지가 0으로 같기 때문에 15≡50(법 5)이기도 합니다.

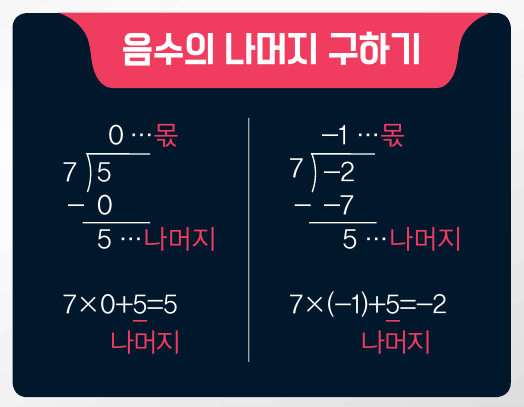
그럼 -2와 5가 7을 법으로 하는 합동인지 확인해봅시다. 이때 -2의 나머지는 어떻게 구할까요? 음수의 나머지는 나눗셈의 검산식을 생각하면 쉽게 구할 수 있습니다. 나누는 수에 몫을 곱하고 나머지를 더했을 때 나오는 수가 나누기 전 수인지 확인하면 되죠. 예를 들면 5를 7로 나눴을 때의 검산식은 7×0+5=5입니다. 이를 음수에 적용하면 -2는 7×(-1)+5이므로 나머지가 5입니다. 따라서 -2와 5는 7을 법으로 하는 합동입니다. 

의혹3 그럼 상은 왜 받은 것일까?

실제로 치카의 판정법은 해외에서도 논란이 되고 있습니다. 치카의 학교 수학 선생님의 동생 사이먼 앨리스는 치카의 판정법을 자신의 블로그에 올렸는데, 그 게시글엔 ‘치카의 판정법이 새롭지 않다’는 댓글이 여러 개 달렸습니다. 또 수학, 과학 질의응답 사이트인 ‘스켑틱스 스택 익스체인지’에서도 ‘치카의 판정법이 새롭냐’는 토론이 벌어졌죠. 결국 앨리스는 자신의 블로그에 치카의 판정법이 기존에 있던 방법과 수학적으로 같다고 해도 치카는 기존 방법을 몰랐기 때문에 치카에게는 새로운 발견이었다고 해명했습니다.

그렇다면 ‘트루 리틀 히어로’는 왜 치카에게 상을 준 것일까요? 김 기자는 치카에게 상을 수여한 ‘트루 리틀 히어로’에 수상 이유를 문의했지만 답변을 받지 못했습니다. 정민주 인하대학교 과학영재교육센터 연구원은 “트루 리틀 히어로는 수학적 권위를 갖는 기관이 아니기 때문에, 스스로 문제 의식을 품고 탐구한 치카의 리더십을 칭찬하는 의미로 상을 줬을 것”이라고 설명했습니다. 

제보자 이서준 학생을 만나다 INTERVIEW

김 기자의 팩트체크 확인 결과 치카의 판정법은 완전하게 새로운 것은 아니었습니다. 
그렇다면 이서준 학생은 이 사실을 어떻게 알았을까요? 직접 이서준 학생의 이야기를 들어봤습니다. 
 
처음 7의 배수 판정법을 알게 된 건 초등학교 3, 4학년쯤 책을 통해서였어요. 처음에 책에서 7의 배수 판정법을 봤을 땐 잘 이해되지 않아서 인터넷에서 찾아봤어요. 그런데 최근에 기본적인 합동식 개념과 7의 배수 판정법 증명을 학원에서 배웠어요. 그 내용을 응용해서 모든 자연수에 대해 판정법을 만들 수 있는지 고민하던 중 수학동아 기사를 보게 됐죠. 그래서 치카의 방법이 기존의 방법과 같다는 것을 쉽게 발견할 수 있었습니다. 

* 용어정리

합동 : 모양과 크기가 똑같아 완전히 포개어지는 두 도형.