d라이브러리

작년 이맘때 퓨처킴은 태국여행을 다녀왔습니다. 하지만 올해는 마크 망치질을 하고 있군요(쓴웃음). 그 추억을 회상하며 태국에서 봤던 수상가옥을 만들어보겠습니다. 그럼 시작 전에 좋아요 꾸욱! 구독 꾸욱! 누르면 수학 시험 100점 맞을지도~?

집을 한 채도 아니고 여러 채 지었더니 정말 힘드네요. 하지만 완성작품을 보니 왕왕 뿌듯합니다. 제 상상력을 더해서 수상가옥끼리 연결하는 다리도 만들었어요. 친한 이웃 집은 자주 왕래할 수 있게 말이죠! 그런데 다리라…, 다리…, 다리? 갑자기 수학 문제가 번뜩였어요! 바로 ‘쾨니히스베르크 다리 문제’요! 

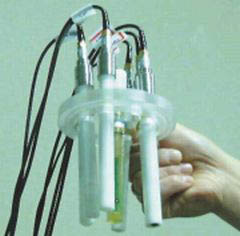
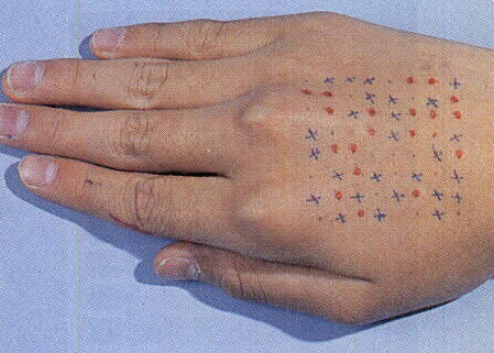
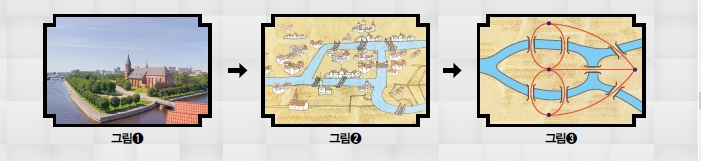
18세기 독일 쾨니히스베르크(현재 러시아 칼리닌그라드)에는 고리 모양으로 흐르는 프레겔 강이 있었습니다. 이 강은 그림➋처럼 도시를 4개의 구역으로 나눴고, 7개의 다리가 이 구역들을 연결했습니다. 다리를 산책하던 사람들은 이런 궁금증이 생겼죠. ‘7개의 다리를 한 번씩만 지나 모든 다리를 건널 수 있을까?’ 당시 수학에 자신 있다는 많은 사람이 도전했지만, 이 문제는 풀지 못했어요. 

한붓그리기가 가능한 조건은?

그런데 1736년 수학계의 거장! 스위스 수학자 레온하르트 오일러가 이 문제에 도전합니다. 오일러는 참신한 방법으로 문제를 해결했는데요, 바로 육지 부분을 점으로, 다리는 선으로 표현하는 거였어요. 오일러는 이 문제를 푸는 데 중요한 것이 다리나 육지의 모양이 아닌 ‘연결 관계’라고 생각했습니다. 그래서 그림➊과 같은 실제 다리를 그림➌처럼 점과 선으로 나타냈죠. 
그리고 보니 쾨니히스베르크 다리 문제는 점 4개와 선 7개가 있는 한붓그리기 문제네요. 한붓그리기란 붓을 한 번도 종이 위에서 떼지 않고 같은 곳을 두 번 지나지 않으면서 모든 점과 선을 들르는 도형을 그릴 수 있느냐 하는 문제예요.
오일러는 고심한 끝에 ‘쾨니히스베르크 다리 문제는 불가능하다’라는 결론을 내립니다. 그리고 이 문제를 푼 것에서 더 나아가 한붓그리기가 가능한 조건을 밝히고 증명하죠. 그 조건은 다음과 같습니다. 

그래프 이론의 시초가 되다!

오일러의 방법이 그다지 참신하지 않다고요? 그건 이미 한붓 그리기를 많이 접해봐서 그래요. 당시에는 획기적이자 매우 위대한 발견이었습니다. 오일러의 한붓그리기가 ‘그래프 이론’의 시초라고 여겨지거든요. 그래서 그래프 이론에서 한붓그리기를  ‘오일러 경로’라고 부릅니다. 
그래프 이론은 지하철 노선도를 보면 이해하기 쉬운데요, 역은 점으로 철길은 선으로 나타내 복잡한 서울 지하철 노선을 한눈에 확인할 수 있죠. 이렇게 연결되어 있는 관계를 그래프로 나타내 그 관계들을 수학적으로 연구하는 것이 그래프 이론이랍니다.

언제나 말 많은 퓨처킴은 오늘은 이 정도로 말을 줄이겠습니다. 대신 여러분께 문제 하나 내죠. 과연 퓨처킴이 만든 수상가옥은 한붓그리기가 가능할까요? 그 답은 유튜브 댓글로 남겨주세요! 

※편집자주 LOL, 오버워치, 배그부터 다양한 인디게임까지 섭렵한 게임 인생 6년 차 퓨처킴. 하지만 마인크래프트는 처음이다. 회사에서 게임하는 것이 조금은 눈치 보이지만 마크의 초고수가 되는 그날까지, 나는 달린다!

참고

달인과 함께하는 마인크래프트 세계 건축 여행 : 아시아와 아프리카