d라이브러리

무엇을 그린 것인지 잘 알 수 없는 작품을 본 적이 있나요? 보이는 것을 그리지 않고 점이나 선, 면 또는 색채와 같은 조형 요소로 구성한 그림을 말이지요. 이런 그림을 ‘추상화’라고 합니다. 오늘은 추상화의 선구자로 불리는 화가, 피에트 몬드리안의 작품을 감상하려고 합니다. 그의 작품은 많은 부분에서 수학과 닮았거든요.

왼쪽 작품을 한번 보시죠. 검은색 선으로 나뉜 사각형에 빨강, 파랑, 노랑의 단순한 색깔로 이뤄져 있습니다. 이 작품을 보면 어떤 생각이 드나요? 

‘이런 건 나도 그리겠네’ 또는 ‘도대체 이 그림은 무엇을 의미할까?’ 이런 생각을 하게 되지 않나요? 아마도 추상화를 봤을 때 대부분 비슷한 생각을 할 것 같습니다. 대체 몬드리안은 왜 이런 그림을 그리게 된 걸까요? 

몬드리안의 나무에서 프랙털을 찾다! 

몬드리안이 처음부터 추상화를 그렸던 건 아니에요. 초기에는 아름다운 풍경 그림을 주로 그렸습니다. 그중에서도 많이 볼 수 있는 것이 바로 ‘나무’입니다. 

1908~1910년 작품인 ‘붉은 나무’와 1916년 작품인 ‘뒤벤드리히 인근의 농장’을 보세요. 어떤가요? 이때만 해도 전혀 추상화의 느낌은 없죠? 살아있는 나무를 보는 것 같은 착각이 들 정도로 나뭇가지를 정교하게 표현했습니다. 

수학의 눈으로 두 작품을 보면 마치 똑같은 패턴이 반복되는 ‘프랙털’ 성질을 갖는 것처럼 보입니다. 프랙털은 ‘조각난 도형’이라는 뜻으로 일부 작은 조각이 전체와 비슷한 기하학적 형태를 말합니다. 해안선, 번개, 뇌의 표면, 구름, 나무 등 자연현상이나 생물에서 발견되곤 하지요. 

그래서일까요? 2017년 타소스 분디스 그리스 파트라이대학교 수학과 교수가 이끄는 연구팀은 몬드리안의 그림에서 복잡하게 뻗어 나간 나뭇가지가 프랙털 성질을 갖는지 분석했습니다. 결론부터 말하자면 두 작품의 나뭇가지에서 모두 프랙털 구조를 발견했습니다. 그리고 두 나뭇가지의 프랙털 차원의 값은 같았습니다. 

프랙털 차원은 자기 복제를 위해 필요한 도형의 수로, 어떤 도형의 길이를 x배 크게 했을 때 도형의 면적이 n배 증가하면 그 도형의 차원(D)을 logxn이라고 정의합니다. 이 값은 대개 1과 2 사이의 값이 나오는데, 값이 클수록 전체와 부분이 닮았다고 볼 수 있습니다. 

이런 프랙털 차원은 어떻게 계산하냐고요? 연구팀은 프랙털 차원을 계산하는 방법으로 ‘사각형 세기 방법’을 골랐습니다. 위와 같이 그림의 일부를 격자로 나타내고, 나무가 차지하는 사각형의 개수를 셉니다. 그림의 같은 부분을 더 촘촘한 격자로 나타내고 사각형의 개수를 센 뒤 두 값을 프랙털 차원을 구하는 식에 대입하면 약 1.75의 값이 나옵니다. 1보다 2에 더 가까운 값이므로, 몬드리안의 나무는 프랙털 성질을 갖는다고 볼 수 있습니다.

추상화는 본질에 다가가기 위한 화가의 노력 

이처럼 정교하게 나무를 그리던 몬드라인이 왜 갑자기 추상 미술을 하게 된 걸까요? 몬드리안이 활동하던 20세기 초반에는 사진이 대중화되고 있었습니다. 아무리 실물과 똑같이 그려도 실물을 그대로 담는 사진이 있으니 이런 그림은 점점 매력을 잃게 됩니다. 자신만의 세계를 담은 그림이 필요했지요. 

몬드리안은 우리가 보는 모든 것에 본질이 있고, 그 본질은 간결하며 조화롭다는 깨달음을 얻습니다. 이런 생각을 처음 반영한 작품이 바로 앞서 본 1930년에 발표한 ‘빨강, 파랑, 노랑의 구성2’입니다. 본질을 향해 다가가기 위해 점점 가지치기하다 보면 결국 수평선과 수직선, 그리고 삼원색인 빨강, 파랑, 노랑만 남는다는 것이지요. 

구체적인 현상에서 보이지 않는 추상의 본질을 향해 가는 몬드리안의 작품 세계는 수학의 성질과 무척 닮았습니다. 처음 수학을 배울 때를 생각해 보세요. 보이는 사물을 세는 것으로 시작해 더하고 빼고 연산합니다. 그러다가 점점 어떤 현상을 문자와 수로 된 가장 간결한 수식으로 표현하지요. 그래서 수학을 공부하는 시간이 점점 길어지면 무엇인지 잘 알 수 없는 추상화를 보는 것 같은 느낌이 듭니다. 간결한 아름다움을 추구한다는 점에서 몬드리안과 수학이 일맥상통하는 것 같군요. 

춤추는 그림, 빅토리 부기우기 

이번에는 몬드리안이 끝내 완성하지 못한 그의 마지막 작품을 살펴보려고 합니다. 언뜻 보면 전통 보자기 같기도 하고, 또 언뜻 보면 알록달록한 색을 입힌 바코드 같아 보이기도 한 이 작품은 ‘빅토리 부기우기’입니다. 

제목이 독특하지요? 유럽에서 활동하던 몬드리안은 2차 세계대전이 일어나자 미국 뉴욕으로 건너갔습니다. 당시 뉴욕에서는 재즈 음악이 유행하고 있었고, 몬드리안은 재즈 음악 ‘부기우기’를 무척 좋아했습니다. 그리고 자신이 사랑하는 음악을 작품으로 나타내고자 했습니다.  

1996년 미국의 건축학자 칼 보빌은 ‘빅토리 부기우기’에 어떤 기하학적 성질이 있는지 알아보기 위해 작품을 이루고 있는 형형색색의 사각형 배열을 분석했습니다. 보빌은 그림에 쓴 색에 번호를 매겨 이 색 배열을 수열로 나타냈지요. 붉은색은 1, 파란색은 2, 노란색은 3, 검은색은 4, 회색은 5로 정한 후, 그림의 첫 번째 줄의 색을 수열로 나타내니 다음과 같았습니다. 

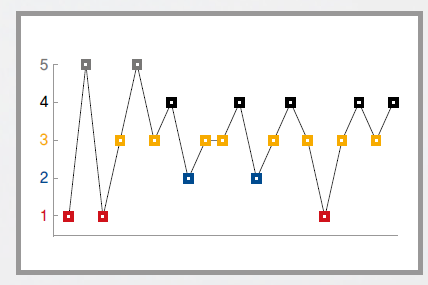
규칙성 없이 1과 5 사이에 숫자들이 움직이고 있죠? 무질서한 선율이라고 생각할 수 있지만, 결국 1과 5 사이의 값 안에서 이런 불규칙함이 반복적으로 이뤄지고 있기에 이 또한 하나의 규칙으로 볼 수도 있습니다. 

어떤가요? 여러분은 이 작품에서 재즈의 향기가 느껴지나요? 재즈의 가장 큰 특징은 그때그때 다른 멜로디로 즉흥 연주하는 것인데, 특유의 리듬과 악기 소리로 이 음악이 재즈라는 걸 나타냅니다. 재즈를 사랑한 몬드리안이 ‘빅토리 부기우기’에 재즈의 이런 면을 표현하고 싶었던 게 아닐까요? 부기우기 음악을 들으며  몬드리안의 작품을 감상해 보세요. 또 다른 매력을 느낄 수 있을 겁니다.