d라이브러리

들러야만 하는 교실들을 점으로, 교실 사이의 길을 선으로 연결하면 회로 모양 그래프가 나와요. 이때 어느 한 점에서 출발해 각 점을 한 번씩만 들르면서 처음 점으로 돌아오는 경로를 찾는 문제를 ‘해밀턴 회로 문제’라고 해요. 견우가 처한 상황과 비슷하죠? 

해밀턴 회로 문제의 해를 탐색하는 방법에는 여러 가지가 있지만 그 중 대표적인 것으로 ‘백트래킹(퇴각검색) 알고리듬’이 있어요. ‘백트래킹’ 기법은 ‘되추적’ 기법이라고도 하는데 간단히 말하면 갈림길이 나올 때마다 표시를 해뒀다가 막힐 때마다 그 갈림길로 되돌아가서 다시 해를 찾는 방법이에요. 경로를 트리 구조로 만들어 따라가며 모든 경우의 수를 따진다고 생각하면 쉬워요. 

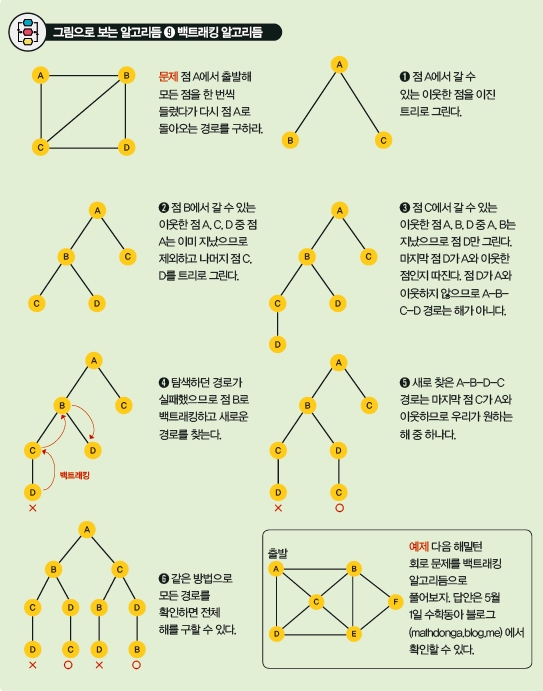
예를 들어 해밀턴 회로 문제는 ‘이웃한 점으로만 이동할 수 있다’, ‘마지막 점이 첫 번째 점과 이웃해야 한다’는 제한 조건에 따라 해당하는 점을 이진 트리로 그려나가는 방법으로 풀 수 있어요.

출발점을 A라고 두면 A에서 갈 수 있는 이웃한 점을 아래에 쓰고 또 그 점에서 이웃한 점 중 기존에 지나지 않은 점들을 계속 써나가는 거예요. 만약 규칙에 어긋나는 지점이 생기면 틀리지 않은 지점까지 한 칸씩 거슬러 올라가며 해를 재탐색하죠. 이런 방법을 ‘백트래킹 알고리듬’이라고 하는데 ‘백트래킹’이라는 용어는 미국 수학자인 데릭 헨리 레머가 1950년대에 처음으로 사용한 뒤 컴퓨터 과학에 널리 쓰이게 됐어요.

백트래킹 알고리듬은 모든 경우의 수를 따져보는 방법이기 때문에 다른 알고리듬에 비해 다소 시간이 많이 걸린다는 단점이 있지만, 해가 있는 문제라면 근사해가 아닌 확실한 답을 찾을 수 있다는 강점도 있지요. 간단한 해밀턴 회로라면 직관적으로 답을 찾을 수도 있지만 회로가 복잡해질수록 정확한 해와 해의 개수를 알기는 어려워요. 이때 백트래킹 기법을 쓰면 정확한 답과 해의 개수도 알 수 있답니다! 견우가 이 설명을 들었으면 금방 경로를 결정할 수 있었을 텐데 사서 고생을 하고 있네요. 그래도 먼저 사과하기 전까진 도와주지 않을 거예요! 

참고자료

문양세 ‘Algorithm-Backtracking’