d라이브러리

까~치까치 설날은 어저께고요, 우~리우리 설날은 떡국 먹는 날이지요! 민족 대명절 설날이 왔습니다. 유행에 민감한 피터팍은 기쁜 날을 맞아 특별히 떡국을 준비해봤습니다. 그런데 떡국이 뜻밖에 아주 수학적이지 뭐예요? 떡국으로 기하학 공부하기, 시작해볼까요?

오래 전부터 우리나라에는 새해 첫날 떡국을 먹는 풍습이 있었습니다. 여기에는 흰 가래떡처럼 건강하고 오래 살라는 의미가 담겨 있습니다. 해가 바뀌는 날 먹다 보니 떡국을 먹으면 한 살 더 먹는다는 이야기도 있는데요, 저는 올해 떡국 안 먹고 한 살 더 안 먹고 싶은데 여러분은 어떠세요? 아직 괜찮다고요? 그럼 가래떡을 좀 더 넉넉히 썰어 볼게요.

떡국을 더 푸짐하게 만드는 타원

떡국떡은 원기둥 가래떡을 비스듬히 썰어 타원으로 자르는 것이 특징입니다. 그런데 왜 하필 타원으로 자르는 걸까요? 피터팍은 여기에서 놀라운 사실을 발견했습니다. 옛 기록을 보면 궁중에서는 떡국을 만들 때 가래떡을 똑바로 썰어 동그란 모양으로 잘랐다는 겁니다! 즉, 어떤 이유가 있어 떡국떡을 타원으로 자르기 시작했다는 뜻이죠.

궁중음식 전문가는 떡국떡 모양이 바뀐 이유가 가난한 백성들이 적은 양으로 더 푸짐한 느낌을 내기 위해서였을 거라고 추측하고 있습니다. 떡을 비스듬히 썰어 타원으로 만들면 같은 양도 확실히 더 많아 보이거든요.

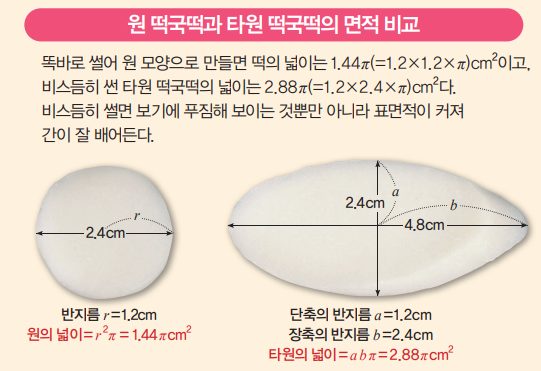
원은 한 점에서 거리가 같은 점이 모여 만들어진 곡선이라 원점을 지나기만 하면 어느 길이나 지름과 같지만, 타원은 단축과 장축으로 이뤄진 도형이라 각도에 따라 지름보다 훨씬 길게 떡국떡을 자를 수 있습니다. 장축이 길수록 면적이 넓어지니까 그릇에 담아두면 훨씬 떡의 양이 많아 보이는 거지요.

타원의 탄생

수학을 정식으로 배우지 않았던 시절에 같은 가래떡의 표면적을 더 크게 할 수 있는 모양이 타원이란 걸 알아낸 조상님들이 대단하죠? 그럼 타원이 어디에서 처음 등장했는지, 타원이란 정확히 어떤 도형인지 조금 더 알아보도록 합시다.

고대 그리스 수학자 아폴로니우스의 저서 ‘원뿔 곡선론’을 보면 그리스어로 ‘부족하다’라는 의미를 지닌 ‘ellipse(타원)’라는 도형이 등장합니다.

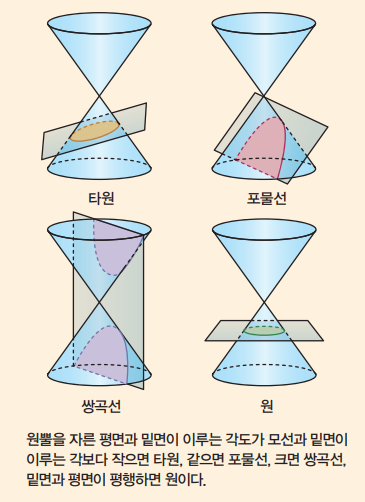
아폴로니우스는 다음 그림과 같이 기울기가 다른 평면으로 원뿔을 잘랐을 때, 이 평면과 원뿔 밑면의 각이 모선과 밑면이 이루는 각보다 작은가, 큰가, 같은가에 따라 도형을 분류했습니다. 모선은 원뿔의 꼭짓점과 밑면의 원둘레의 한 점을 이은 선입니다. 타원은 이 중에서 모선과 밑면이 이루는 각보다 작은 경우이므로 ‘부족하다’는 이름이 붙은 거지요.

하지만 아폴로니우스는 단순히 수학적 흥미로 원뿔 곡선을 연구했을 뿐, 타원을 실생활에 활용하거나 문제를 해결하는 데 쓰지는 않았습니다. 타원이 본격적으로 연구되고 세상의 많은 분야에 응용하기 시작한 건 2천여 년이나 지난 17세기에 이르러서였습니다.

케플러, 우주의 원리를 타원으로 설명하다

천문학에서 인류에게 가장 충격을 준 발견은 코페르니쿠스의 지동설일 겁니다. 그런데 지동설 말고도 큰 파장을 일으킨 우주의 비밀이 또 있습니다. 독일의 수학자이자 천문학자인 요하네스 케플러가 발표한 ‘케플러의 법칙’입니다. 케플러의 법칙에 따르면 태양계의 모든 행성의 공전 궤도가 태양을 초점으로 두는 타원이라는 거였죠!

당시 사람들은 행성이 태양을 중심으로 완전한 원을 따라 움직인다고 믿고 있었습니다. 케플러 본인도 그랬고요. 하지만 스승인 티코 브라헤가 남긴 방대한 관측 자료를 수학적으로 분석한 결과, 원 궤도로는 행성의 움직임을 설명할 수 없다는 결론에 이르렀습니다. 우주의 비밀을 풀려면 새로운 태양계 모형이 필요했죠.

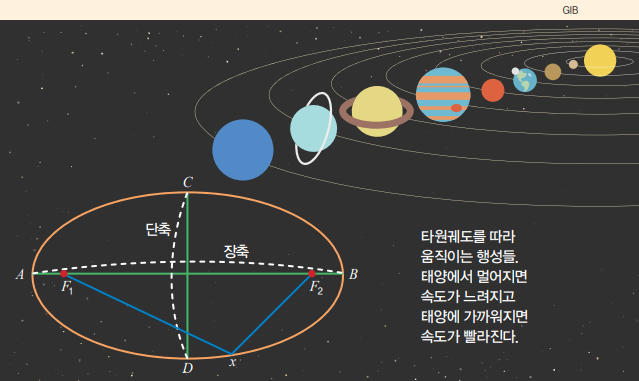
고민 끝에 케플러는 이 문제를 해결할 열쇠가 타원이라는 사실을 알아냅니다. 두 점에서의 거리의 합이 일정한 점들의 집합, 즉 타원으로 궤도를 계산하자 태양과 행성의 거리가 변하는 이유, 어떤 지점에서는 행성의 움직임이 빨라지고 어떤 지점에서는 느려지는 이유 등을 설명할 수 있었습니다.

행성이 타원으로 움직인다는 발견은 원운동을 이상적인 우주의 원리라 믿었던 당시 학계를 놀라게 한 획기적인 발상이었습니다. 하지만 2000년 전에 그리스 수학자들이 원뿔 곡선에 흥미를 느끼고 연구하지 않았다면 케플러가 타원 궤도를 떠올릴 수 없었을지도 모르죠. 그러니 여러분도 무엇이든 수학으로 탐구하는 취미를 가져보세요. 혹시 아나요? 몇천 년 뒤에 우주를 뒤흔들 발견이 될지!

수학과 함께라면 떡국떡을 썰다가도 우주의 비밀에 다가갈 수 있다는 걸 알았으니 이번 설에는 떡국 한 입 먹을 때마다 타원의 정의와 특징을 떠올려 봅시다. 떡국 한 입, 타원 한 입, 떡국 두 입, 타원 두 입…. 타원 한 사발과 함께하는 민족 대명절! 멋지군요.

여러분 제가 떡국을 조사하다가 ‘떡국 무한 굴레’란 걸 발견했습니다. 떡국에 들어가는 떡은 ‘떡국떡’이니까 떡국떡으로 만든 국은 떡국떡국이고, 떡국떡국의 재료는 떡국떡국떡이고 그걸로 만든 국은 떡국떡국떡국이고…(이하 생략). 이걸 보고 있으니 제가 떡국떡인지 떡국떡이 저인지 알 수 없는 무한의 굴레에 빠져드는군요. 여러분도 해보세요. 떡국떡국떡국에 들어가는 떡은 떡국떡국떡국떡, 그러면 떡국떡국떡국떡으로 만든 국은….