d라이브러리

안녕하세요. 피터팍(피터팬+Park)입니다. 요리 실력이 영원히 어린아이에 머물러있어서 붙은 별명이죠. 언젠가 요리 네버랜드를 떠나 당당한 셰프로 성장할 수 있기를 바라며, 여러분 저와 함께해주시겠어요?

스파게티 면을 아무리 구부려도 딱 2조각으로 쪼개지지 않는다니! 뭔가 특별한 이유가 있는 것이 틀림없습니다. 궁금한 건 꼭 수학으로 밝혀내야만 직성이 풀리는 저 수(數)셰프 피터팍이 마른 스파게티 면을 낱낱이 조사했습니다. 앗, 그랬더니 놀라운 사실이 드러났습니다! 이 질문이 이미 물리학자와 수학자 사이에서 꽤 이름난 문제라는군요. 일명 ‘스파게티 미스터리’라고 말이죠.

파인만도 못 푼 ‘스파게티 미스터리’

노벨상을 받은 미국 물리학자 리처드 파인만은 어느 날 친구와 저녁 식사를 준비하다가 이런 궁금증이 생겼습니다. 

‘왜 마른 스파게티 면은 절대 2개로 쪼개지지 않는 걸까?’

간단한 질문이었지만 답은 쉽게 떠오르지 않았습니다. 파인만과 컴퓨터과학자인 친구 대니얼 힐리스는 고민에 빠졌죠. 두 사람은 요리는 제쳐두고 저녁 시간 내내 스파게티 면을 2개로 쪼개기 위해 온갖 이론과 방법을 동원해 실험하기 시작했습니다. 물에서도 쪼개보고, 식탁에 놓고 한 손으로 누르고 한 손으로 끝을 쳐보고, 간격을 바꿔가며 쪼개봤지만 결국 답은 찾지 못했습니다. 주방만 온통 스파게티 면으로 더러워졌을 뿐이었죠.  

알버트 아인슈타인과 함께 20세기 최고의 물리학자라고 꼽히는 파인만이 풀지 못하는 스파게티 문제라니! 흥미를 느낀 학자들은 스파게티 면 2개로 쪼개기에 도전하기 시작했습니다. 하지만 도통 성공하지 못하면서 이 문제는 ‘스파게티 미스터리’라는 별칭을 얻게 됐죠. 

진전이 없는 것처럼 보였던 스파게티 미스터리연구가 풀리기 시작한 건 수십 년이 지난 2005년이었습니다. 프랑스 에꼴폴리테크 교수인 바질 오돌리와 세바스티엥 노이커치가 스파게티 면을 2개로 쪼갤 수 없는 이유를 수학적으로 설명하는 논문을 발표한 겁니다.

평범한 막대 모양 물체를 떠올려보죠. 마침 눈에 띄는 이 나무젓가락이 좋겠군요. 나무젓가락의 양 끝을 잡고 천천히 힘을 준다고 생각해봅시다. 어느 정도까지는 휘어지지만, 한계를 지나는 순간 부러지겠죠? 나무젓가락이 견딜 수 있는 ‘곡률’이 한계를 넘어섰기 때문입니다. 곡률은 곡선이 얼마나 휘었는지 나타내는 기울기 변화율입니다. 

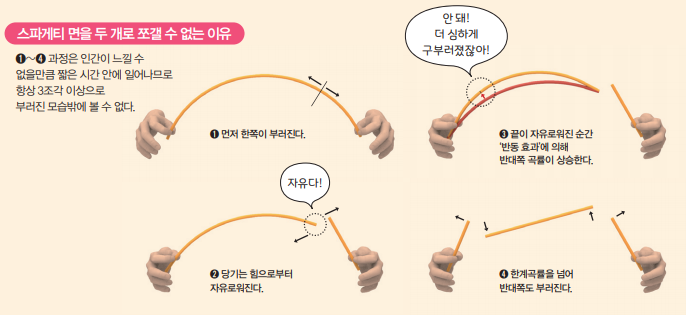
보통 막대기 모양 물체는 한계보다 많이 구부러지는 순간 두 동강이 납니다. 가장 심하게 휘어졌던 부분이 끊어져 힘으로부터 자유로워지면, 다시 곡률이 낮아지며 원래 상태로 돌아가는 거죠. 그런데 스파게티 면은 조금 달랐습니다.

스파게티 면은 오히려 부러지는 순간 반대쪽이 더 심하게 휘었습니다. 원래 구부러졌던 정도보다 훨씬 곡률이 커지면서 반대편도 한계점을 넘어버렸던 겁니다! 한쪽을 자르면 반대쪽도 부러져버리니 스파게티 면은 절대 2조각이 될 수 없었던 거죠. 오돌리는 이런 현상을 이상적인 유체에서 단단한 물체의 움직임을 설명하는 ‘키르히호프 방정식’을 통해 설명하고 ‘반동 효과’라고 불렀습니다.

자, 이로써 스파게티 면은 절대 2개로 쪼갤 수 없다는 결론에 도달했군요. 하지만 정말 그럴까요?

수십 년의 난제, 마침내 수학자가 풀다

끝난 것 같았던 이 문제에 다시금 도전한 건 수학자였습니다. 미국 매사추세츠공과대학교(MIT) 수학과 연구원인 로널드 헤이저와 에드가 그리델로는 면을 배배 꼬아서 구부리면 반으로 쪼개지는 경우가 있다는 걸 알아냈습니다. 꼬임이 첫 번째 절단이 일어날 때 반동 효과를 낮춰줬던 겁니다.

아이디어를 찾은 연구팀은 이 현상을 설명하고 정확히 계산할 수 있는 수학 모형을 세우기 위해 또 다른 MIT 수학자 비샬 파틸을 팀에 들였습니다. 

직접 만든 기계로 꼬임 각도와 간격을 분석하길 수백 번, 연구팀은 드디어 스파게티 미스터리를 풀 수학 모형을 완성했습니다. 어떤 종류의 스파게티 면이든 정확하게 반으로 쪼개는 방법을 계산할 수 있게 된 거죠! 또한 이 모형으로 13년 전 오돌리와 노이커치가 발표했던 논문도 이론적으로 설명할 수 있었습니다.

보통 판매되는 24cm 길이의 스파게티 면은 250° 꼬인 상태에서 구부리면 된다고 하니, 여러분도 집에 스파게티 면이 있다면 실험해 보세요!

알고 보니 냄비에 스파게티 면을 넣을 땐 부러뜨리는 게 아니라 부채처럼 기울여서 펼치면 된다고 하네요. ‘머쓱타드’. 하지만 우리는 그냥 부러뜨리기로 해요. 파인만의 난제를 떠올리며 수학자의 해법을 직접 확인해볼 좋은 기회니까요. 무엇을 상상하든 그 이하의 요리상식을 보여주는 피터팍은 다음에 더 맛있는 수학 이야기로 돌아오겠습니다. 안녕~!