d라이브러리

# 편집자 주
이름만 보고서는 정체를 알 수 없는 수학 정리가 있다! 특이한 이름의 수학 정리에 재미있는 이름이 붙게 된 유래와 함께 수학적 의미를 살펴봅니다. 기사를 읽기 전에 어떤 수학 정리인지 추측해 보면 더 재밌을 거예요!

할머니가 오빠와 저에게 맛있는 간식을 만들어 주셨어요. 미션은 싸우지 말고 정확히 반으로 나눠 먹기! 단, 칼은 한 번만 쓸 수 있다! 바나나 팬케이크와 초콜릿 팬케이크, 햄 샌드위치 모두 정확히 반으로 나눌 수 있을까요? 그 순간, 오빠와 나는 서로 눈치를 보기 시작합니다. 수학 요정이여, 간식을 정확히 나눠 오빠와 전쟁을 치르는 일은 없도록 도와주소서!

평화롭게 지내던 남매의 의가 상하는 꼴을 볼 수 없어 수학이라는 학문이 생긴 건 아닐까 싶습니다. 수학으로는 팬케이크가 삐뚤빼뚤한 모양이라도, 단 한 번의 칼질이면 딱 절반으로 나눌 수 있습니다.

팬케이크 절반으로 자르는 완벽한 방법

다른 맛 팬케이크를 두 개씩 만들어 주셨다면 아무 문제가 없었을 것인데, 할머니가 왜 남매에게 이런 시련을 주셨는지 모르겠어요. 하지만 직사각형이든, 삼각형이든 심지어 찌그러진 원모양이라도 수학 요정과 함께라면 문제없으니 걱정하지 마세요.

이제 접시 위에 납작한 팬케이크 두 개가 놓여 있습니다. 마치 직선처럼 보이는 실처럼 얇은 칼을 이용하면 초콜릿 팬케이크 하나는 절반으로 자를 수 있는 순간은 늘 있습니다. 직선의 방향에 상관없이요!

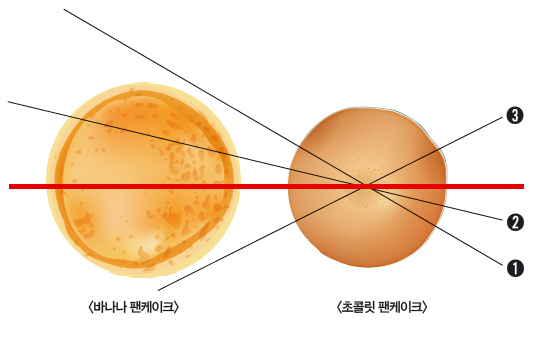
그런데 ➊번처럼 칼질하면 초콜릿 팬케이크는 절반으로 나눠지지만 바나나 팬케이크는 0:100으로 완전히 불공평하게 나뉘네요.

직선을 조금 회전해 ➋번처럼 칼질하면 어떨까요? 아까보다는 낫지만 여전히 불공평합니다. 아래쪽은 전체의 80%정도, 위쪽은 20% 정도밖에 안 돼 보이거든요. ➌번처럼 칼질을 하면 처음의 경우와 완전히 반대로 아래쪽을 가져가려던 사람이 하나도 못 먹게 됩니다.

그럼 ➊번 직선과 ➌번 직선 사이에 어느 순간에는 빨간 직선처럼 절반으로 나뉘는 지점이 있겠네요. 그 지점을 찾아 칼질하면 한 번에 두 팬케이크를 정확하게 절반으로 나눠먹을 수 있답니다. 아하! 2차원 평면에서, 마치 평면처럼 납작한 2개의 물체는 1차원 직선으로 정확히 반씩 나뉘네요.

도전! 햄 샌드위치 나누기!

이번엔 빵 2개와 햄 1장으로 만든 샌드위치입니다. 팬케이크는 납작했으니 실처럼 얇은 칼로 자를 수 있었지요. 그러나 햄 샌드위치는 3개의 물체로 만들어진 음식으로, 완전한 3차원 물체입니다.

이 경우 아까와 다르게 생각해야 합니다. 팬케이크를 자르는 것과 비슷하지만, 차원을 다르게요. 3차원 물체인 빵과 햄이 행성처럼 둥둥 떠 있고, 세물체를 2차원 평면으로 자른다고 상상해 보세요. 물체와 평면의 위치가 적절하면 세 물체를 정확히 반씩 나눌 수 있을 겁니다. 이 방법으로 햄 샌드위치도 정확히 절반으로 나눌 수 있는 것이고요.

이 문제는 폴란드의 수학자 후고 스테인하우스가 1938년 처음 떠올렸는데, 이후 1945년 같은 나라의 스테판 바나흐라는 수학자가 ‘보석 울람 정리’라는 위상수학의 이론을 이용해 증명했습니다. 이를 ‘햄 샌드위치 정리’라고 부릅니다.

혹시 눈치 채셨나요? 햄 샌드위치 정리는 3차원에 해당하는 특별한 경우이고, 팬케이크 정리는 2차원에 해당하는 경우이며 이것은 다음과 같이 n차원으로 일반화할 수 있습니다.

‘n차원 공간에 있는 n개로 된 물체는 n-1차원의 초평면★으로 정확히 반으로 나뉜다.’

초평면★
전체 공간보다 한 차원 낮은 공간. 평면에서는 직선이 초평면이고, 공간에서는 평면이 초평면이다.

3차원 공간에 있던 2개의 빵과 1개의 햄, 총 3개 물체로 이뤄진 햄 샌드위치는 2차원의 평면 칼로 정확히 반 나눌 수 있습니다. 일반화된 식을 이용하면, 만약 7차원 공간에 있는 7개로 된 물체는 6차원의 칼로 똑같이 반으로 나눌 수 있을 겁니다. 4차원 이상은 우리 머리로 상상하기 힘들지만, 이론상으로는 가능합니다.

이렇게 열심히 설명하고 있는데, 벌써 다 먹었다고요…? 수학 요정은 한 남매의 평화를 지킨 것으로 만족할게요.