d라이브러리

단 한 명의 시청자만 있어도 최선을 다하는 수학동아TV! 안녕하세요! BJ맹추입니다. 두 번째 방송에서 다룰 수학 개념은 특집 기사에 등장하는 ‘대칭’입니다. 대칭은 주변에서 흔히 사용하는 말이지요. 그러나 흔할수록 눈여겨 보지 않는 법. 오늘 방송을 보면 그동안 몰랐던 대칭의 숨은 이야기가 속속 등장할 거예요! 자, 그럼 채널~고정!

무엇이 무엇이 똑같을까♪

대칭에 관해 자세히 말하기 전에 먼저 대칭하면 무엇이 떠오르는지 말해보죠. 중·고등학생이라면 교과서에 등장하는 대칭이동, 점 대칭, 선 대칭이 떠올랐겠지만, 보통은 거울에 비친 사물이나 미술 시간에 배운 데칼코마니, 길 양옆에 서 있는 가로수가 생각날 거예요. 이들의 공통점은 뭔가를 기준으로 좌우에 ‘똑같은’ 대상이 있고, 뭔가 질서정연한 느낌이 든다는 겁니다.

우리가 어렴풋이 알고 있는 이 대칭이 과연 정확한지 확인하기 위해 진부하지만 ‘대칭’의 어원을 살펴볼게요. 대칭(symmetry)은 ‘같다’(sym)는 뜻과 ‘측정한다’(metry)는 뜻으로 이뤄져 있는데, 이 말은 기준으로부터 어떤 대상까지의 거리를 측정하면 동시에 대칭인 대상까지의 거리를 함께 측정한 것과 같다는 거예요. 아직도 조금 애매한가요? 그럼 수학에서는 대칭을 뭐라고 정의하고 있는지 살펴보죠!

그래서 ‘대칭’이 뭐야? 딱 말해!

수학에서는 대칭을 뭐라고 말하는지 알면 깜짝 놀랄 수도 있어요. 여러분을 위해 제가 찾아온 대칭의 정의를 읽어 보겠습니다.

“어떤 대상에 작용을 가해서 원래 모습과 변하지 않을 때, 이 대상은 대칭을 갖는다고 말한다….”

잠깐! 제가 아주 쉬운 예를 들어 설명해볼 테니 채널 돌리는 그 손을 10초만 멈춰주세요. 설명을 들으면 아마 ‘아~, 그렇구나’라고 외칠지도 모른다니까요.

먼저 여러분과 제 사이에 앞, 뒤 색이 같은 정삼각형이 놓여있다고 생각해 봅시다. 이제 여러분이 잠시 눈을 감고 있는 동안 제가 이 삼각형에 어떤 ‘행위’를 할 거예요. 뭘 해도 상관없지만, 조건이 있습니다. 반드시 뭔가 해야 한다는 것과 여러분이 눈을 떴을 때 삼각형이 움직였다는 사실을 눈치 채면 안 된다는 겁니다. 다시 말하면, 삼각형을 움직이긴 하는데 처음과 상태가 똑같아 보여야 하는 거지요!

삼각형을 이리저리 움직이다 보면 시계 또는 반시계 방향으로 적당히 회전하거나 뒤집는 방법 밖엔 없을 거예요. 이런 행위가 위에서 말한 작용이고, 이런 행위가 가능하다면 그 대상은 대칭을 갖는다고 말하는 거죠. 이제 이해가 가시나요?

방정식을 여는 열쇠가 대칭?

어차피 원래 모습과 달라지는 게 없다면 가만있는 삼각형을 왜 움직이냐고요? 언뜻 보면 의미 없는 장난을 하는 것 같지만, 수학에서 대칭은 도형보다 방정식과 관련이 많답니다.

15세기 초 은행이 처음 생기면서 사람들은 이자계산 문제에 관심을 갖기 시작했어요. 이자를 계산하려면 1차, 2차는 물론 5차방정식의 해까지 구해야 했지요. 그런데 4차방정식까지는 해를 구하는 ‘근의 공식’을 찾았지만 5차방정식은 도저히 근의 공식을 구할 수 없었어요.

이때 프랑스의 천재 수학자 에바리스트 갈루아가 등장해 ‘5차방정식의 근의 공식은 없다’라는 갈루아 이론을 발표합니다. 갈루아는 어떤 집합의 원소는 그대로 둔 채 순서만 바꿔주는 함수의 집합을 고안해, 5차방정식의 해는 근의 공식으로 구할 수 없다는 사실을 밝혔는데, 이 함수 집합이 바로 ‘대칭군’이랍니다.

5차방정식의 해를 구하려다 대칭을 수학적으로 다룬 갈루아 이론은 대수학의 핵심인 ‘군론’으로 발전했어요.

티 좀 내는 게 어때?

이제 대칭에 대해 좀 알았으니 평면도형이 어떤 대칭을 갖고 있는지 살펴보도록 하죠! 좀 전에 예로 든 정삼각형은 회전해서 원래 모양으로 돌아오는 ‘회전대칭’과 뒤집어서 원래 모양으로 돌아오는 ‘반사대칭’이 있다고 했어요. 그런데 회전은 얼마나 회전했느냐, 반사는 무엇을 기준으로 반사했느냐에 따라 다양합니다.

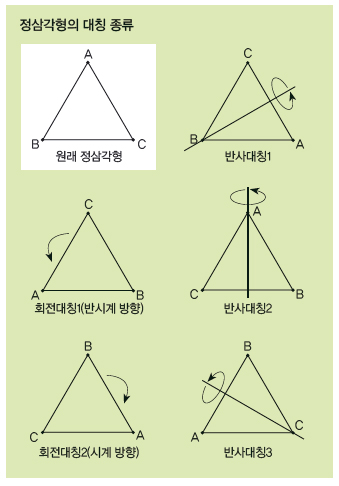
정삼각형은 먼저 시계 방향과 반시계 방향으로 각각 120° 회전하면 원래 모양과 겹치므로 회전대칭은 2개고, 각 꼭짓점에서 마주보는 변에 수직으로 내린 선을 기준으로 뒤집으면 되니까 반사대칭은 3개예요.

모양이 다른 정사각형의 경우 정삼각형과 비슷하게 생각해보세요. 회전대칭은 4개, 반사대칭 역시 4개가 있어요. 대칭을 해도 티가 나지 않기 때문에, 달라 보이지만 실제로는 같은 대칭을 중복해서 세는 경우가 많아요. 대칭을 잘 찾는 팁은 한 꼭짓점을 기준으로 대칭했을 때, 이 꼭짓점이 어디로 옮겨가는지 잘 살펴보는 거예요. 다들 헷갈리지 말고 잘 찾을 수 있도록!

수학의 주기율표, 대칭

수헬리베붕탄질산플네나마…. 뜬금없이 뭔 소리냐고요? 화학 시간에 배운 주기율표의 원소들을 순서대로 외우고 있는 겁니다. 대칭 얘기하다가 갑자기 웬 주기율표냐고 하시겠지만, 대칭도 주기율표와 비슷한 점이 많답니다.

주기율표를 보면 여러 원소가 결합해 새로운 물질을 만들지요. 수학에서는 1과 자신만 약수로 갖는 ‘소수’가 비슷한 역할을 합니다. 복잡한 화합물을 쪼개면 결국 주기율표에 있는 원소들로 분해되는 것처럼 아무리 큰 자연수도 여러 소수의 곱으로 표현되니까요. 여러 소수를 곱하는 것을 한 대상에 여러 대칭을 반복 적용하는 것으로 생각하면 서로 다른 대칭을 이용해 새로운 대칭을 만들 수 있어요.

정15각형을 예로 들어볼게요. 정15각형의 회전대칭은 정삼각형과 정오각형의 회전대칭을 반복적용해서 만들 수 있습니다. 아래 왼쪽 그림처럼 정15각형의 꼭짓점 A가 B로 이동하려면, 정오각형이 360°×1/5=72°만큼 회전하는 대칭을 두 번 적용한 뒤(①), 정삼각형을 360°×1/3=120°만큼 반시계 방향으로 돌리면(②) 정15각형을 360°×1/15 =24°만큼 회전하는 대칭을 만들 수 있어요.

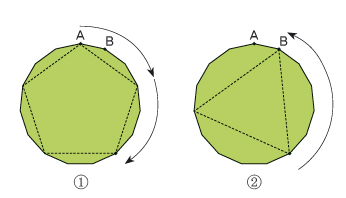
360°를 기준으로 어떤 비율만큼 회전했는지에 주목하면 3과 5가 15의 소인수이고, 따라서 1/15=2/5-1/3이 성립하기 때문에 정15각형의 대칭을 만들어낼 수 있는 거예요. 결국 대칭이 소수와 연관이 돼서 대칭도 마찬가지로 주기율표의 원소 같은 역할을 할 수 있는 거지요.

유희수학으로 유명한 수학자 ‘존 콘웨이’는 이렇게 원소 역할을 하는 대칭을 찾아 대칭의 주기율표를 만들고 있다고 해요. 대칭은 광물의 결정 모양을 분류하거나 패턴이 있는 벽지 문양을 만들 때처럼 다양한 분야에 쓰입니다. 대칭의 주기율표가 완성되면 아직 과학이 밝혀내지 못한 사실을 수학이 밝혀낼 수 있지 않을까요?