d라이브러리

여러분은 슬링키를 어떤 방법으로 즐기나요? 보통 양손으로 슬링키를 잡고 저글링을 하듯이 위아래로 손을 엇갈려 움직이며 코일이 오른쪽, 왼쪽으로 쏠리도록 하는 동작을 반복해요. 그런데 슬링키를 제대로 즐기려면 계단에 굴려야 한대요.

슬링키를 계단에서 떨어뜨리면 우당탕탕 내려 오거나 그냥 뚝 떨어져 멈추는 다른 물체와 달리, 이제 걸음마를 시작한 아이처럼 몸을 늘렸다 줄였다 하면서 차근차근 내려오거든요. 이 광경은 많은 어린이의 마음을 사로잡았답니다. 슬링키는 왜 이렇게 움직이는 걸까요?

실수로 발명한 슬링키
1943년 미국의 선박 회사에서 기계공학전문가로 일하던 리처드 제임스는 거친 파도에도 끄떡없이 떠 있게 해줄 기계 장비를 개발하는 일을 하고 있었어요. 어느 날 실수로 높은 선반에서 용수철 하나를 떨어뜨렸는데, 이 용수철이 선반에서 탁자 위의 책으로, 탁자로, 바닥으로 자연스럽게 건너뛰는 게 아니겠어요.

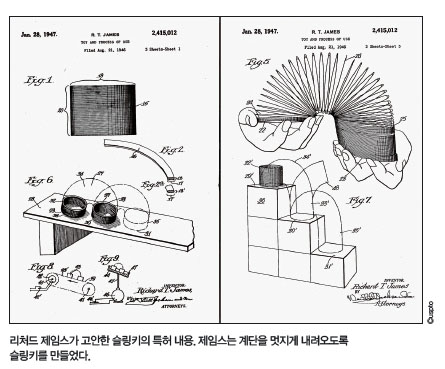
이 모습이 신기했던 제임스는 용수철의 낙하운동을 잘 활용하면 재밌는 장난감을 만들 수 있겠다는 생각에 여러 종류의 철사를 감았다 풀었다 하며 계단을 멋지게 내려오는 장난감 개발에 꼬박 1년을 매진했어요. 그 결과 특허까지 받아 시중에 선보일 수 있었어요.

시장의 반응은 대성공! 처음 만든 400개가 단숨에 팔려나갔고, 출시 2년 만에 세계적으로 사랑받는 장난감 반열에 올라 밀려드는 주문을 소화하기 위해 슬링키를 만드는 기계까지 고안했답니다. 70년 동안 세계적으로 3억 개가 팔렸다고 하니 정말 대단하지요?

슬링키가 잘 엉키는 까닭은?!

슬링키의 단점 중 하나가 잘 엉킨다는 거예요. 가지고 놀려고 보면 어느새 자기들끼리 엉켜 어떻게
풀어야 할지 막막하게 만들어요. 그런데 이런 슬링키의 엉킴이 위상수학과 관련 있다는 내용이 수
학 질문 사이트 ‘매스매틱스 스택 익스체인지’에 올라왔어요.

아이디 weux082690은 DNA의 꼬임과 같은 원리로 슬링키가 엉켰기 때문에 그 원리를 이용해 엉킴을 풀 수 있다고 주장했어요. 어떤 뜻인지 자세히 살펴볼게요.

줄 하나를 양 손으로 잡고 한쪽 방향으로 계속해서 돌려요. 그러면 어느 순간 그림처럼 끈 전체가 서로 엉키기 시작해요. 그 이유는 고리수=꼬임수+비틀림수(75쪽 고리수와 꼬임수, 비틀림수의 관계 참고)를 만족하기 때문이에요. 줄을 꼬기 시작하면 꼬임수가 증가해요. 줄의 끝을 고정하면 고리수는 절대 변하지 않기 때문에 전체를 엉키게 만드는 비틀림이 꼬임과 다른 방향으로 많아지는 거예요. 이는 실험을 통해서도 확인할 수 있고, 수학적으로도 계산할 수 있어요. DNA는 이 같은 원리로 꼬여 이중 나선 구조를 이룹니다.

아이디 weux082690의 주장에 따르면 슬링키도 고리수=꼬임수+비틀림수를 만족하기 위해 엉켰대요. 슬링키를 가지고 놀다가 자기도 모르게 줄로 고리를 만드는 행동(고리수 증가)을 하게 되고, 그것이 반복되다 보니 서로 엉키고 말았다(비틀림수 증가)는 거지요.

이같은 모습은 유선 전화선의 엉킴에서도 나타난다고 주장했어요. 한 손으로만 전화를 받으면 문제가 없는데, 통화 중에 전화기를 받는 손을 바꾸기도 하고 매번 다른 손으로 전화를 받으면서 은연중에 전화선을 교차하게 만들어 어느 순간 줄 전체를 엉키게 만들었다는 거예요. 따라서 반대로 선을 교차시키면 자동으로 엉킴이 풀린다고 주장했어요.

과연 이 말은 수학적으로 신빙성이 있을까요? 박경배 고등과학원 연구원은 “수학적으로는 설명이 되지만, 현실에선 이렇게 슬링키의 엉킴을 푸는 건 쉽지 않다”고 설명했어요. 슬링키의 재질이 단단한 플라스틱이나 철이라 실제로 엉킴을 풀 수는 없다는 거예요. 하지만 전화선처럼 말랑말랑한 재질로 만든 줄은 weux082690의 주장대로 반대 방향으로 줄을 돌리기만 해도 전체 엉킴을 풀 수 있다고 설명했어요.

혹시 모르니, 잠자고 있던 슬링키를 꺼내 돌려 봐야겠어요. 제멋대로 엉킨 슬링키가 풀리는 기적이 일어나길 바라면서요.