d라이브러리

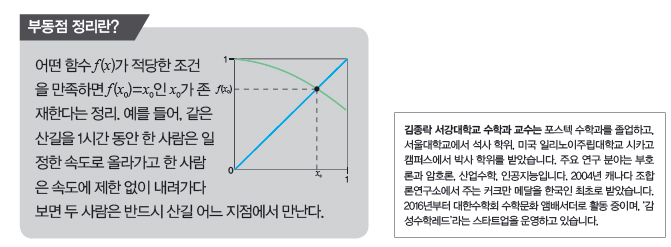
매일 이용하던 지하철의 운행이 중단됐을 때 허겁지겁 다른 노선을 찾아본 경험이 있나요? 지하철은 여러 노선이 얽혀있어서 출발역과 도착역을 잇는 노선 중 아무거나 골라 타면 도착역에 갈 수 있어요. 만약 새로 찾은 노선도 운행이 중단됐다면 또 다른 경로를 찾으면 되지요.

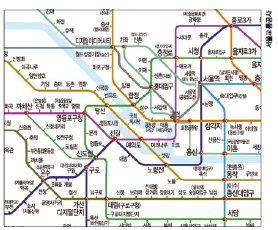
끊긴 노선을 피해 새로운 경로를 찾는 모습이 꼭 게임을 하는 것 같습니다. 오늘 소개할 ‘스위칭 게임’이 바로 이런 방식으로 즐기는 게임이에요. 스위칭 게임은 1951년경 미국의 수학자이자 공학자인 클로드 섀넌이 만들었어요. 섀넌은 여러 컴퓨터를 이어주는 통신선 중 하나가 끊겼을 때 주변에 있는 통신선을 이용해 우회하는 방법을 찾다가 스위칭 게임을 떠올렸어요.

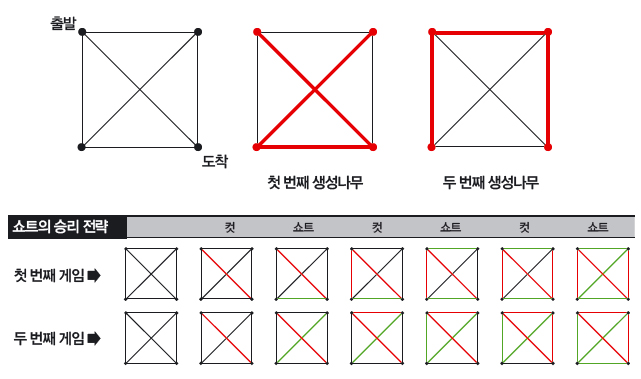
스위칭 게임은 보통 사각형 격자 그래프 위에서 진행합니다. 먼저 그래프 위에 있는 두 점을 출발점과 도착점으로 정하고, 한 사람은 그래프의 변을 하나씩 색칠하는 쇼트(short), 다른 한 사람은 변을 지우는 컷(cut)을 맡습니다. 여기서 변이란 이웃한 두 점을 연결한 선이에요. 이제 쇼트는 변을 색칠해 출발점과 도착점을 잇는 길을 만들어야 하고, 컷은 쇼트가 길을 만들지 못 하도록 방해해야 합니다.

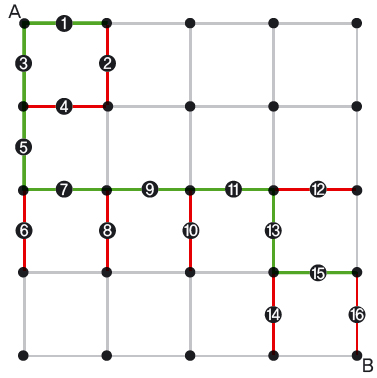
왼쪽 가로세로에 점이 5개씩 있는 격자에서 하는 스위칭 게임을 보세요. 쇼트(녹색)는 변을 색칠해 출발점 A에서 도착점 B를 잇는 길을 만들어가고, 컷(빨간색)은 쇼트가 길을 잇지 못하도록 변을 지웁니다. 왼쪽은 결국 컷이 16번째 변을 지우면서 쇼트가 도착점으로 가는 마지막 경로를 차단했기 때문에 컷이 이긴 게임이에요.

스위칭 게임에서 이기려면 어떻게 해야 할까요? 수학동아 10월호 ‘보드게임 페스타’에 나온 촘프와 마찬가지로 스위칭 게임도 구체적으로 어떤 변을 색칠하거나 지워야 이길 수 있는지 밝혀져 있지 않아요. 다만 컷이 먼저 시작하고, 그래프가 어떤 조건을 만족하는 경우 ‘쇼트가 이기는 방법이 반드시 존재한다’는 사실이 알려져 있을 뿐입니다. 1964년 수학자 알프레드 레먼은 그래프 이론을 이용해 컷이 먼저 시작하는 스위칭 게임에서 쇼트가 항상 이기려면 아래와 같은 조건이 필요하다는 사실을 밝혔어요.

생성나무는 그래프와 관련된 수학 개념으로, 어떤 그래프가 있을 때 그래프 위의 모든 점, 그리고 몇 개의 변만 색칠해 새로 만든 그래프를 뜻해요. 단 새로 만든 그래프는 반드시 순환 고리가 없어야 하고 색칠한 변으로 연결돼 있어야 해요. 즉, 한 점에서 출발해 어떤 경로를 택해서 움직이더라도 출발점으로 다시 돌아올 수 없고, 두 점을 선택했을 때 두 점을 연결하는 경로가 반드시 있어야 합니다.

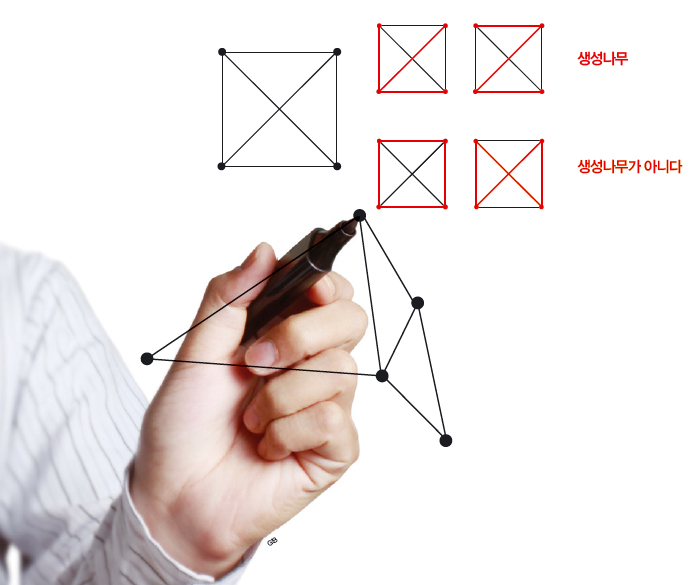
레먼에 따르면 그래프에서 색칠한 변이 겹치지 않는 생성나무를 두 개 이상 찾을 수 있으면 쇼트가 항상 이길 수 있어요. 점과 변이 많은 그래프에서는 이길 수 있는 방법을 찾기가 어려우니 위에 점이 총 4개, 변이 6개인 그래프에서 정말 쇼트가 이길 수 있는지 확인해 볼게요. 물론, 이기는 전략을 찾기 전에 먼저 변이 겹치지 않는 두 개의 생성나무를 찾아야겠죠?

스위칭 게임과 닮은 브릿짓과 헥스
모습은 다르지만, 스위칭 게임과 방식이 비슷한 게임으로 ‘브릿짓’과 ‘헥스’가 있어요. 보드게임 페스타를 열심히 읽는 독자라면 브릿짓이 낯설지 않을 거예요. 브릿짓은 촘프를 만든 데이비드 게일이 만든 게임으로, 스위칭 게임과 달리 변 없이 점만 세로로 n개, 가로로 n+1개 있는 격자를 이용합니다. 크기가 같은 격자를 시계 방향으로 90° 돌려서 원래 격자와 포갠 뒤에 게임을 한다는 점이 독특합니다.

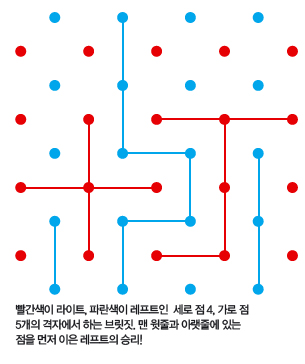
게임 규칙은 이렇습니다. 먼저 원래 격자에서 게임을 할 사람을 라이트, 90° 돌린 격자에서 게임을 할 사람을 레프트라고 정합니다. 레프트는 맨 위에 있는 n개의 점 중 하나를 출발점으로 선택해 맨 아래에 있는 점까지 선을 이어야 하고, 라이트는 맨 왼쪽에 있는 점에서 맨 오른쪽에 있는 점을 이어야 합니다.

레프트와 라이트는 가로세로 방향으로 선이 겹치지 않게 그리면서 먼저 선을 이어야 이길 수 있습니다. 격자를 떨어뜨려 놓고 보면 두 사람이 동시에 길을 만드는 스위칭 게임으로 볼 수 있습니다. 상대가 그리는 경로가 선분과 겹치면 안 된다는 게 스위칭 게임에서 컷이 경로를 지우는 것과 같으니까요.

헥스는 정육각형으로 이뤄진 마름모 보드판 위에서 하는 게임으로, 브릿짓과 비슷하게 마주 보는 두 변에 붙어있는 정육각형을 먼저 연결하는 사람이 이깁니다. 다른 점이 있다면 선을 연결하는 대신 두 사람이 각자 말을 정육각형 위에 올려놓아 연결한다는 겁니다.

노벨상의 일등공신, 헥스
헥스는 1940년대에 덴마크의 공학자이자 시인인 피엣 헤인과 게임이론으로 유명한 존 내시가 각각 독자적으로 개발했습니다. 존 내시는 헥스를 개발했을 뿐 아니라 헥스에서 처음 말을 두는 사람이 반드시 이길 수 있다는 사실을 밝혔고, 헥스는 절대 비기는 경우가 없다는 ‘헥스 정리’를 증명하기도 했습니다.

헥스 정리에 따르면 굳이 양 끝 정육각형을 이어서 이기려 하지 않고 상대편 말이 이어지는 걸 막다 보면 저절로 이길 수 있습니다. 비기는 경우가 없으니 한 사람이 변 위의 정육각형을 잇지 못해 게임에서 지면 반드시 다른 사람이 이겨야 할 테니까요.

놀라운 사실은 헥스 정리가 존 내시에게 노벨 경제학상을 받게 한 일등공신이라는 점입니다. 내시는 헥스 정리와 부동점 정리가 내용은 달라 보여도 사실은 같은 뜻이라는 걸 밝혔어요. 따라서 헥스 정리가 참이니 부동점 정리도 참이 되고, 부동점 정리를 이용해 게임이론의 핵심내용인 ‘내시 균형이 항상 존재’한다는 사실을 밝힐 수 있었죠.

수학에서는 재미있는 게임이 때때로 엄청난 발견으로 이어집니다. 여러분도 게임을 수학적으로 분석하다 보면 새로운 이론을 발견하게 될지도 몰라요!