d라이브러리

2차원에서 어느 두 직선을 골라도 사잇각이 같은 직선 3개는 쉽게 찾을 수 있습니다. 사잇각이 60°가 되게 그리면 되지요. 하지만 4개만 되도 사잇각이 다른 두 개가 반드시 나와 불가능합니다. 즉 평면에서는 사잇각이 일정한 직선 수의 최댓값이 3입니다.
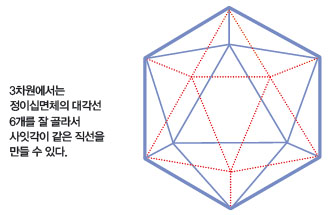3차원에선 어떨까요? 2차원보다는 구하기 어렵지만 그렇다고 아주 어려운 건 아닙니다. 1948년 네덜란드 수학자 요하네스 한티어스는 3차원에서는 최대 6개까지 가능하다는 것을 증명했습니다.

정이십면체의 대각선 중 6개를 잘 고르면 사잇각이 일정하게 만들 수 있다는 거지요. 한티어스는 한걸음 더 나아가 4차원에서도 3차원과 같은 상황에서 직선 6개가 만들어지고, 이게 최대라는 걸 밝혔습니다.

 

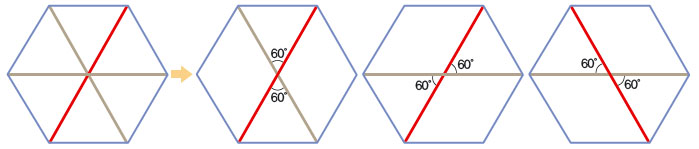
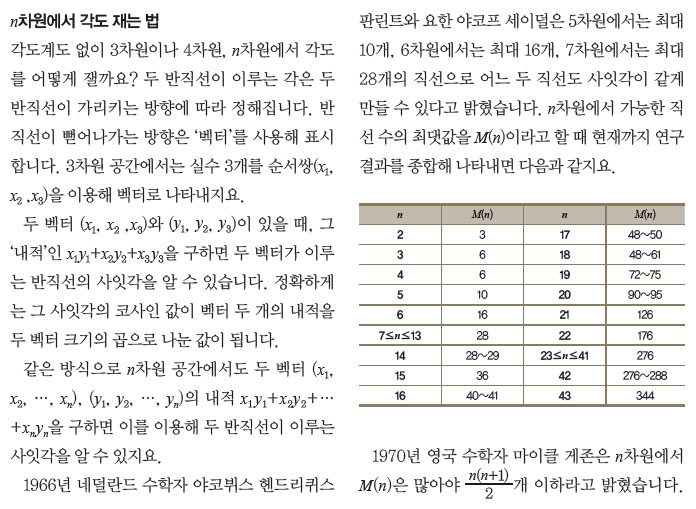
해결의 열쇠는 램지정리
이번 연구를 이끈 수다코브 교수는 2015년 연구에 관한 부크 교수의 강연을 듣고 이 문제에 관심을 가지기 시작했습니다. 사실 부크 교수는 수다코브 교수의 제자입니다. 그리고 이번에 논문을 같이 쓴 세 사람 모두 수다코브 교수의 제자지요. 수다코브 교수는 그해 한 학기 동안 옥스퍼드대에서 머물렀는데, 거기에 다른 제자인 키바쉬 교수가 있어서 함께 문제를 풀었습니다. 그리고 스위스로 돌아와 현재 지도 학생인 발라와 드렉슬러와 함께 연구를 이어간 것이지요.

이 문제를 풀기 위해 연구팀은 각 직선을 길이 1인 벡터로 나타낸 다음 이 벡터들 사이의 내적을 구했습니다. 이는 행렬로 나타나는데, 두 직선의 사잇각이 일정하면 행렬의 대각선은 모두 1이고 나머지 항은 cos x 혹은 -cos x 값을 갖습니다. 여기서 부호를 보고 그래프를 만든 뒤 램지정리(수학동아 2017년 1월호 ‘따끈따끈한 수학’ 참고)를 이용해 답을 구했습니다.

이 문제에도 아직 수학자가 해결하지 못한 부분이 많이 남아 있습니다. 당장 14차원에서 답이 무엇인지 아직도 모릅니다. 과연 14차원에서 최댓값은 29일까요? 각이 고정된 경우에 1.93n보다 더 작게 할 수 있을까요? 여러분도 한 번 생각해 보세요.


엄상일 교수는 KAIST 수학과를 졸업하고, 미국 프린스턴대에서 박사 학위를 받았습니다. 현재는 KAIST에서 강의와 연구를 하고 있습니다. 그래프이론과 이산수학, 조합적 최적화가 주요 연구 분야입니다. 2012년에는 젊은과학자상(대통령상)을 수상했고, 2013년에는 한림선도과학자로 선정됐습니다.