구독상품안내
미남, 미녀를 가리는 기준으로 얼굴의 좌우 대칭을 들기도 하죠? 아름다움의 기준은 수학에서도 똑같이 적용돼요. 수학자는 점 대칭, 선 대칭, 거울 대칭, 회전 대칭 등 대칭이 많은 도형을 아름답다고 생각했어요. 그래서 대칭이 가장 많은 도형이 무엇인지 찾는 연구를 했어요.
이번 호에서는 어떤 그림을 그리든 좌우 또는 상하 대칭인 모습으로 그림을 그려 주는 프로그램을 만들어 볼 거예요.
대칭이라고 하면 나비처럼 좌우가 같은 것만 떠오르죠? 하지만 수학에서는 회전 이동, 반사와 같은 변환GIB 했을 때 원래 상태로 돌아오는 것을 대칭이라고 불러요. 여기서 반사는 대칭축을 중심으로 반 접었을 때 같은 모양이 되는 거예요.
예를 들어 볼까요? 정삼각형을 떠올리고, 120° 회전해 보세요. 여전히 정삼각형이죠? 따라서 정삼각형은 120° 회전 변환을 해도 모양이 같은 대칭 도형이에요. 사실 정삼각형에는 이 밖에도 5가지 대칭이 더 숨어 있어요. 240°, 360° 회전 이동과 한 꼭짓점과 마주보는 대변의 중심을 이은 직선을 대칭축으로 하는 3가지 반사가 그 주인공이에요.
수학자들은 도형마다 몇 가지 대칭이 숨어 있는지 알아봤어요. 입체도형 중에서 가장 기본이 되는 정육면체의 대칭은 48가지, 4차원 초입방체는 384가지나 됐어요.
그렇다면 대칭이 가장 많은 도형은 무엇일까요? 또 몇 개나 될까요? 수학자들은 이 물음에 답하기 위해서 오랫동안 연구했어요.
해답은 독일의 수학자 베른트 피셔가 찾았어요. 피셔는 거울에 비친 모습은 반드시 대칭이 된다는 점에 착안해 꼭짓점을 거울이라고 가정하고 도형을 만들기 시작했어요. 거울 13,571,955,000개를 설치하자 더 이상 새로운 거울을 둘 자리가 없었어요. 이렇게 만든 도형의 대칭을 따지자 무려 4,154,781,481,226,426,191,177,580,544,000,000가지나 됐어요. 정말 어마어마하죠?
그런데 얼마 지나지 않아 미국의 수학자 봅 그리스가 이보다 더 큰 도형이 있을 수도 있다고 주장했어요. 그리스와 피셔가 함께 연구한 끝에 대칭의 개수가 무려 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000가지나 되는 도형을 발견했어요. 대칭의 개수가 몇 개인지 읽을 수조차 없는 이 도형은 196,883차원에서 볼 수 있어요. 이 도형을 발견한 피셔조차도 어떤 모양인지 상상이 가지 않아 ‘몬스터’라는 이름을 붙여줬어요.
그렇다면 대칭이 가장 많은 도형은 무엇일까요? 또 몇 개나 될까요? 수학자들은 이 물음에 답하기 위해서 오랫동안 연구했어요.
해답은 독일의 수학자 베른트 피셔가 찾았어요. 피셔는 거울에 비친 모습은 반드시 대칭이 된다는 점에 착안해 꼭짓점을 거울이라고 가정하고 도형을 만들기 시작했어요. 거울 13,571,955,000개를 설치하자 더 이상 새로운 거울을 둘 자리가 없었어요. 이렇게 만든 도형의 대칭을 따지자 무려 4,154,781,481,226,426,191,177,580,544,000,000가지나 됐어요. 정말 어마어마하죠?
그런데 얼마 지나지 않아 미국의 수학자 봅 그리스가 이보다 더 큰 도형이 있을 수도 있다고 주장했어요. 그리스와 피셔가 함께 연구한 끝에 대칭의 개수가 무려 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000가지나 되는 도형을 발견했어요. 대칭의 개수가 몇 개인지 읽을 수조차 없는 이 도형은 196,883차원에서 볼 수 있어요. 이 도형을 발견한 피셔조차도 어떤 모양인지 상상이 가지 않아 ‘몬스터’라는 이름을 붙여줬어요.
➊ 대칭축 오브젝트와 연필 오브젝트, 글상자 오브젝트를 3개 만들어요. 글상자의 이름을 각각 ‘좌우 대칭’, ‘상하 대칭’, ‘설명’으로 변경해요. 오브젝트 각각을 보기 좋게 배치합니다.
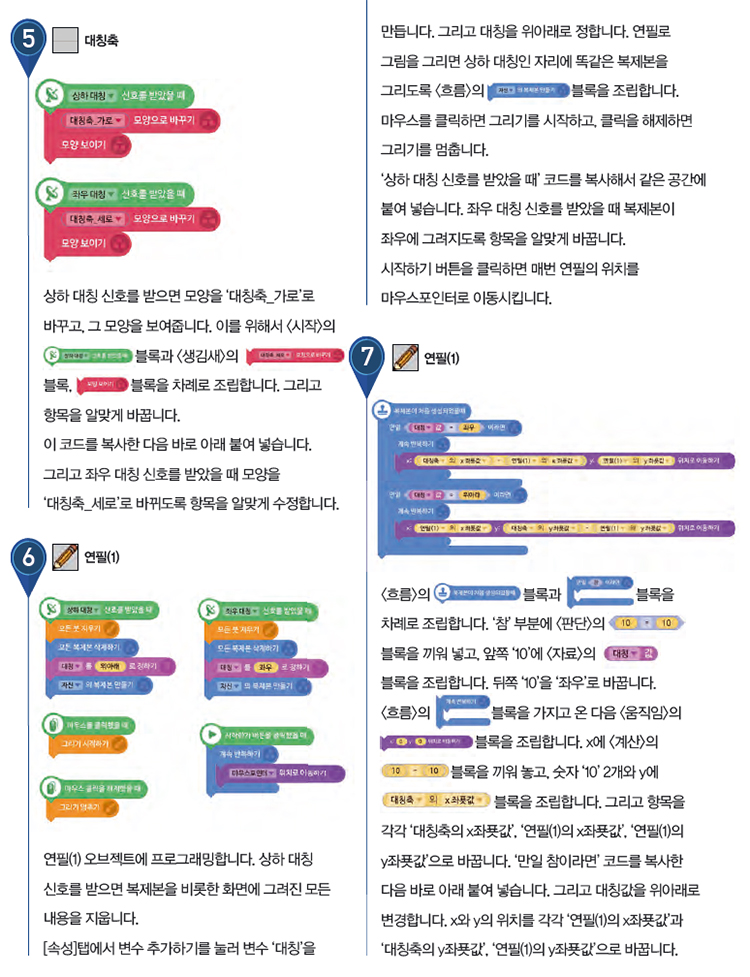
➋ ‘좌우 대칭’ 글상자를 클릭하면 화면에 그려진 모든 내용을 지우고, 대칭축 모양을 세로로 바꿉니다.
➌ ‘상하 대칭’ 글상자를 클릭하면 화면에 그려진 모든 내용을 지우고, 대칭축 모양을 가로로 바꿉니다.
➍ 연필 오브젝트의 복제본을 만듭니다.
➎ 복제본의 위치는 대칭축을 기준으로 연필 오브젝트에 대칭인 곳으로 정합니다. 좌우 대칭일 때 x값은 대칭축의 x값에서 연필의 x값을 뺀 값입니다. y값은 연필의 y값 그대로입니다. 반대로 상하 대칭일 때는 x값은 그대로고, y값은 대칭축 y값에서 연필의 y값을 뺀 값입니다.
➏ 마우스를 클릭하면 연필 오브젝트와 복제본에서 동시에 그림을 그립니다.
➐ 마우스 클릭을 멈추면 연필 오브젝트와 복제본에서 동시에 그리기를 멈춥니다.
엔트리 홈페이지(play-entry.org) ‘학습하기’ 코너에서 ‘오픈 강의’를 클릭한 뒤 검색창에 ‘수학동아 11월호’를 검색해 보세요! 그러면 대칭 프로그램을 조금 더 쉽게 프로그래밍할 수 있어요. 화면 구성과 프로그래밍에 필요한 변수가 기본으로 저장돼 있어 블록을 이용해 알고리즘만 짜면 되기 때문이에요. 앞으로 학습하기 코너를 많이 이용해 주세요!
