
모르는 사람들끼리만 시험 보려면?
저르퍼시의 추측
최근 영국 옥스퍼드대 알렉스 스콧 교수와 미국 프린스턴대 폴 세이머 교수가 30년 묵은 난제 ‘저르퍼시의 추측’을 풀었습니다. 저르퍼시의 추측은 1985년 헝가리의 수학자 언드라시 저르퍼시가 제기한 추측으로, 모르는 사람들끼리만 시험을 치려면 시험장이 몇 개 있어야 하는지 묻는 문제입니다. 그동안 수학자들은 이 문제를 어떻게 연구해 왔는지, 앞으로 어떤 연구가 이어질지 알아봅시다.
학생 N명이 수학경시대회에 응시했습니다. 서로 아는 학생들은 같은 시험장에서 시험을 볼 수 없다고 할 때 시험장은 최소 몇 개 있어야 할까요?
서로 아는 사이인지 미리 조사해 놓는다면 시험장이 최소 몇 개가 필요한지 알 수 있습니다. 모두 서로 모르는 사이라면 시험장이 한 개만 필요할 테고, 최악의 경우 N개가 필요할 수도 있습니다. {재석, 준하, 명수, 동훈, 광희}처럼 서로 아는 사이인 학생들의 집합 중에서 원소가 가장 많은 집합의 학생수를 P라고 하면 시험장은 적어도 P개 이상 필요합니다.
만일 P≤2인 경우, 즉 서로 아는 사이인 세 명의 학생이 없다면 어떨까요? 막연하게 생각해 보면 N(학생수)이 아무리 커도 시험장은 아주 많을 필요가 없을 것 같습니다. 하지만 60년 전 그래프의 이론의 선구자 중 한 명인 캐나다의 수학자 윌리엄튀테는 시험장의 개수가 10100보다 작으면 시험을 치를 수 없는 상황이 생긴다고 밝혔습니다. 게다가 10100을 어떠한 큰 수로 바꾸더라도 결론은 동일하다는 것을 밝혔지요.
시험장이 P개일 조건은?
학생수와 상관없이 시험장의 수가 적은 경우는 없을까요? 있다면 그렇게 되는 조건이 있을까요? 1960년 프랑스 수학자 클로드 베지는 다음 두 질문의 답이 모두 ‘아니오’라면 P개의 시험장으로 충분하다고 추측했습니다. 이를 ‘완벽그래프에 관한 강한 추측’이라고 합니다.
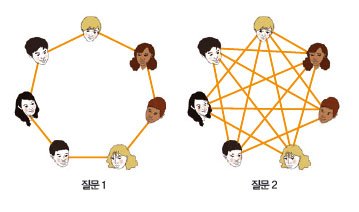
❷ 5명 이상의 홀수인 m명의 학생을 잘 뽑아서 동그랗게 앉힌다. 이때 이웃한 학생끼리는 서로 모르는 사이고, 이웃하지 않은 학생끼리는 서로 아는 사이인 경우가 있는가?
완벽그래프에 관한 강한 추측은 매우 어려운 문제입니다. 추측이 제기되고 46년이 지난 2006년에야 179쪽에 달하는 논문으로 해결됐습니다. 마리아 처드노프스키, 폴 세이머, 닐 로버트슨, 로빈 토마스 이렇게 4명의 수학자가 몇 년 동안 노력한 끝에 질문 1, 2의 답이 모두 ‘아니오’인 경우에는 P개의 시험장만 준비하면 된다는 것을 증명한 것입니다. 수학자들은 질문의 답이 ‘아니오’인 모든 경우를 다 따져 이런 결론을 이끌어냈습니다.

저르퍼시의 추측이란?
시험장의 개수가 정확히 P가 아니라 P에 관한 함숫값 이하로 되는 경우도 찾을 수 있을까요? 즉 학생수 N이 매우 클 때 시험장의 개수를 P에 관한 식으로 나타낼 수 있는지 묻는 겁니다.
1985년 헝가리 수학자 언드라시 저르퍼시는 질문 2의 답이 무엇이든 간에 질문 1의 답만 ‘아니오’라면 N의 크기에 상관없이 P에 관한 어떤 함수만큼만 시험장을 준비하면 된다고 추측했습니다. 다시 말해 질문 1의 답이 ‘아니오’인 경우 P100이라든지, 100P, PP처럼 어떤 적당한 P에 관한 함수만큼의 시험장만 준비하면 된다는 것이지요. 이게 바로‘저르퍼시의 추측’입니다.
그런데 최근 영국 옥스퍼드대 알렉스 스콧 교수와 미국 프린스턴대 폴 세이머 교수가 저르퍼시의 추측을 해결했습니다. 질문 1의 답이 ‘아니오’인 경우, 22P+2개의 시험장만 있으면 된다는 것을 증명한 것이지요. 조만간 어느 저널에 논문이 실릴 예정입니다. 그런데 논문이 15쪽으로 매우 짧아 많은 수학자들이 놀랐습니다. 현재 두 수학자는 후속 연구로 이와 관련된 더 어려운 문제, 다른 저르퍼시의 추측을 해결하고 있습니다.
저르퍼시의 추측은 그래프 색칠 문제로 바꿔 생각해 볼 수가 있습니다. 시험을 보는 N명의 학생 하나하나를 꼭짓점으로, 서로 아는 사이인 학생들을 선으로 연결하면 그래프가 됩니다. 이제 그래프의 꼭짓점을 색칠하면 되는데, 단 조건이 있습니다. 선으로 연결돼 있는 두 꼭짓점은 같은 색으로 칠할 수 없는 것이지요. 이때 필요한 최소 색깔을 그래프의 ‘채색수’라고 하고, 이런 문제를 ‘그래프 색칠 문제’라고 합니다.
그래프 색칠 문제 중에 가장 잘 알려진 문제는 ‘4색 문제’입니다. 지도의 각 영역을 꼭짓점, 국경을 맞대고 있는 이웃한 나라는 선으로 연결해 나타낸 평면그래프의 채색수가 항상 4 이하라는 것을 증명하라는 문제로, 1852년에 제기됐습니다. 무려 100년 동안 풀리지 않다가 지난 1976년 케네스 아펠과 볼프강 하켄이 컴퓨터를 이용해 증명했습니다.


그래프 색칠 문제는 여러 분야에 쓰입니다. 예를들어 라디오 방송을 위해선 최소 몇 개의 주파수가 필요한지 구할 때 쓰입니다. 라디오 송신탑의 거리가 가까우면 혼선이 일어날 수 있기 때문이지요. 고속버스 회사가 정해진 버스 노선의 시간표를 모두 운행하고자 할 때 필요한 최소 버스 수를 구할때도 그래프 색칠 문제로 바꿔 문제를 해결합니다.
이처럼 그래프 이론에는 실생활에 유용한 문제가 많지만 오랫동안 풀리지 않은 문제 또한 많지요. 여러분도 한 번 자기만의 생각을 가지고 시도해 보세요. 어쩌면 누구도 생각지 못한 새로운 아이디어로 사람들을 깜짝 놀라게 할 수도 있습니다.












