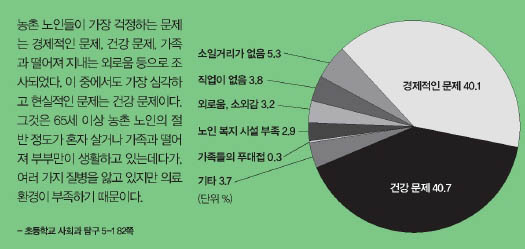
오늘 함께 이야기하려는 게임은 핀란드의 로비오 엔터테인먼트가 만든 ‘앵그리버드’예요. 이름에서 알 수 있듯이 눈썹이 V자에 부리를 삐죽거리는 화난 새들이 나옵니다. 알을 훔쳐간 돼지들을 응징하기 위해 직접 새총에 올라탔대요.
휴대전화 스크린에 손가락을 대고 새총을 잡아당긴 뒤, 손가락을 떼어 새총을 놓는 방법으로 새를 쏘아 돼지 탑을 맞힙니다. 새총을 제대로 튕기면 한 방에 돼지 탑이 무너지기도 하고, 또는 무너진 돼지 탑이 연쇄적으로 다른 탑을 무너뜨리기도 합니다. 하지만 아무렇게나 새총을 튕겼다가는 새가 돼지 탑까지 날아가지 못하거나 힘이 너무 약한 탓에 부딪치기만 하고 떨어져버립니다.
앵그리버드 스페이스 버전까지 깨면서 나만의 노하우가 생겼어요. 새총을 어떤 방향으로 얼마나 당기냐에 따라 새가 날아가는 포물선의 크기와 방향, 부딪히는 힘이 달라진다는 것이었지요. 나도 모르게 수학적인 직감을 이용했다고나 할까요?
 새가 튕겨나가는 순간의 ‘앵그리 벡터’
새가 튕겨나가는 순간의 ‘앵그리 벡터’미국 텍사스대 수학교육과의 존 램 교수는 앵그리버드의 원리를 수학으로 설명했어요. 그는 새총을 튕겼을 때 빨간 새가 날아가는 포물선 궤적을 이차함수로 나타냈습니다.
램 교수는 2차원 좌표에서 새가 출발하는 위치를 (0, 0)로 정했어요. 새가 가장 높이 날아오른지점, 즉 포물선의 꼭짓점은 (20.2, 4.8)이었지요. 그리고 새가 지나는 다른 지점의 좌표를 고려해보면, 새가 날아가면서 그리는 포물선 궤적은 f(x)=-0.0118x2+0.47672x입니다(상수는 0에 가까워서 생략합니다).

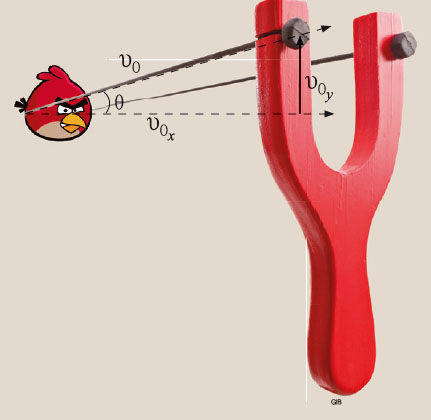
램 교수는 새총을 당기는 각도와 길이에 따라새가 날아가는 방향이나 궤적뿐 아니라 블록에 부딪히는 힘의 크기도 달라진다며 ‘앵그리 벡터’로 표현했어요. 그리고 새총에서 새가 튕겨 나가는 현상을 삼각함수로 설명했습니다. 새총을 잡아당겼을 때 지표면과의 각도(θ)를 이용해 새가 처음에 튕겨나가는 초기속도(υ0)를 구한 것입니다.
새가 (x, y) 좌표에 놓여 있다고 생각하고, 초기속도도 앞으로 나아가는 방향과 수직으로 올라가는 방향으로 나눠 υ0x와 υ0y로 정했어요. 초기속도는 삼각함수로 설명했어요. υ0x= υ0 cosθ, υ0y= υ0sinθ처럼 말이지요(오른쪽 그림). 그리고 시간(t)에 따라 달라지는 새의 위치는 다음과 같아요.

이렇게 구한 식들을 공통된 변수로 묶고 하나로 합쳐, 새총을 약 25°로 당겼을 때 1초당 약22.5864앵그리의 속도로 새가 튕겨져 나간다는 결론을 얻었습니다.
게임 노하우는 바로 직감적인 수학 능력!
앵그리버드에서는 빨간 새 외의 여러 가지 새가 색깔별로 운동 변환을 해요. 예를 들어 하얀 새는 커다란 알을 떨어뜨린 뒤 다시 작은 포물선 운동을 시작하고, 노란 새는 특정 지점으로부터 도착지까지 빠르게 직선으로 내리꽂히지요.
이런 운동도 수학식으로 나타낼 수 있습니다. 하지만 우리는 하나하나 계산하지 않아도 어느 지점에서 스크린을 눌러 운동을 변환시켜야 돼지 탑을 효율적으로 무너뜨릴 수 있을지 예상할 수 있습니다. 또 단계별로 점점 어려워져도 각각의 새를 어떻게 이용해야 할지 스스로 깨닫습니다. 게임 단계만 올라가는 것이 아니라, 직감적인 수학 능력이 늘고 있었던 셈이지요.
그 사이 버터맥주에서 모락모락 피어오르던 김이 사라졌네요. 다음에는 더 맛있는 음료와 함께 더 재미난 이야기로 만나기로 해요.