냄새 맡다=향기 분자와 후각 수용체가 결합한다
최 순경 : 실종된 지 4일째인 패션모델을 찾아야 해. 용의자는 연쇄 살인범인데, 이전 범죄에서 항상 실종 5일째에 피해자를 살해했으니 서둘러야 해. 경기도 양평에 있는 모 마을회관 마당에서 실종자의 지갑이 발견됐어. 지갑이 발견된 지점 가까이 있는 뒷산을 수색하는 데 경찰들이 총동원될 거야. 그런데 오초림 너, 냄새를 보는 게 확실한 거지?
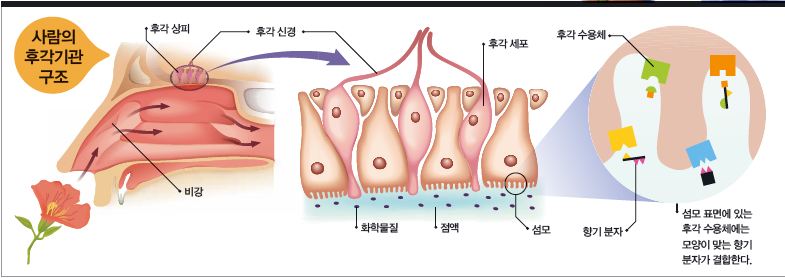
제가 보통 사람들과 어떻게 다른지 알려드릴게요. 사람의 콧구멍 안쪽에는 ‘비강’이라는 빈 공간이 있어요. 공기가 코로 들어오면 비강에서 먼지 같은 이물질을 걸러내요. 비강의 천장에는 축축한 점막이 있어요. 이 점막을 ‘후각 상피’라고 해요. 이곳엔 냄새를 감지하는 후각 세포(뉴런)가 있고요. 후각 세포의 한쪽 끝은 비강 쪽으로 나와 있고 다른 한 쪽은 뇌로 연결돼요.
비강 쪽 후각 세포 끝에는 ‘섬모’라는 솜털이 있어요. 바로 이 섬모 표면에 있는 후각 수용체와 향기 분자가 결합하는 거예요. 냄새를 맡으면, 냄새가 콧구멍을 지나 후각 상피에 도착해요. 냄새는 콧물로 축축한 후각 상피에 녹아들죠. 그러면 냄새에 섞여 있던 향기 분자가 자기와 맞는 후각 수용체와 각각 결합해요. 후각 수용체는 향기 분자와 만나면 전기신호를 만들어 뇌로 보내요. 그러면 무슨 냄새를 맡은 건지 알 수 있답니다.
사람의 후각 세포는 약 500만 개예요. 사람보다 후각이 발달한 개는 후각 세포가 2억개가 넘어요. 후각 세포에서 향기 분자와 결합하는 후각 수용체는 300~400종류예요. 후각 수용체의 모양에 따라 결합하는 향기 분자가 다르대요. 예를 들어, 달콤한 향기를 내는 분자와 기름 향기를 내는 분자는 서로 다른 후각 수용체와 결합해요.
보통 사람들은 이런 방식으로 냄새를 맡지만 특이하게도, 전 냄새 분자가 보여요.
오초림 : 실종자의 지갑에서는 물방울 모양, 개 모양의 향기 분자가 보여요. 산이 아니라 강가에 있던 걸 개가 물어다가 마을회관 앞으로 가져온 것 같아요. 산이 아니라 강가를 수색해야 해요!
행렬의 곱으로 냄새를 본다고?
최 순경 : 강력계에 산이 아니라 강을 중심으로 수색해야 한다고 말했더니 비웃음만 샀어. 개가 실종자의 지갑을 물고 강가에서 마을회관까지 1km 넘게 걸어서 마당의 잘 보이는 곳에 갖다놨다는 게 말이 되냐는 거지. 지갑에서 나는 물비린내는 일반인들이 분간할 수 없을 정도니 냄새를 맡은 거라고 해도 믿지 않을 거야. 냄새를 봤다는 건 더 믿지 않을 거고. 물비린내가 난다는 걸 설명할 다른 방법을 찾아야 해.
오초림 : 방법이 한 가지 있긴 해요. 제가 언젠가 이런 일이 생길까봐 행렬 공부를 열심히 해 뒀거든요. 행렬의 곱을 쓰면 가능해요. 먼저 행렬과 행렬의 곱셈에 대해 알려드릴게요.
수학에서 ‘행렬’이란, 숫자나 기호 등을 네모꼴로 배열해 괄호([ ])로 묶은 걸 말해요. 행렬은 주로 두 항목의 관계를 나타낼 때 써요. 예를 들어,

이 행렬은 농구에서 초림이가 5점, 무각이가 6점을 얻었고 축구에서는 초림이와 무각이가 모두 2점을 얻었다는 뜻이에요.

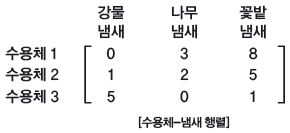
강물, 나무, 꽃밭 냄새를 각각 맡을 때 서로 다른 후각 수용체 3개의 반응도 행렬로 나타낼 수 있어요. [수용체-냄새 행렬]은 후각 수용체 1, 2, 3이 냄새에 반응하는 정도를 수의 크기로 표현한 행렬이에요. 강물 냄새를 맡았을 땐 수용체 3이 전기신호를 많이 만들었고, 나무 냄새를 맡았을 땐 수용체 1과 수용체 2가 반응해요. 또 꽃밭 냄새에는 세 종류의 수용체가 모두 반응하네요.
오초림 : 그런데 냄새는 여러 가지 향기 분자가 섞여서 나는 거예요. 꽃밭에서 한 가지 향기만 나지는 않잖아요? 즉, 이 행렬만으로는 각 수용체가 어떤 향기 분자와 결합하는지 볼 수 없어요. 문제 해결의 열쇠는 바로 ‘행렬의 곱셈’이랍니다.


곱해서 [수용체-냄새 행렬]이 되는 행렬 2개를 찾으면 특정 향기를 내는 분자가 어느 후각 수용체와 결합하는지 볼 수 있지요! 곱셈이 가능한 꼴의 행렬 가운데 제가 찾은 두 행렬은 이거예요.

‘비린 향’, ‘풀 향기’는 세 가지 냄새 속에 섞여 있다고 추측할 수 있는 향이예요. [행렬 1]과 [행렬 2]를 곱해서 나온 행렬은 [수용체-냄새 행렬]과 비슷해요. 곱해서 원래 행렬이 되는 두 행렬을 찾는 건 어려워요. 그러니 곱한 결과가 원래 행렬과 가장 차이가 적은 두 행렬을 찾아야 한답니다.
[행렬 1]을 보면 후각 수용체가 어떤 향기 분자와 결합하는지 알 수 있어요. 수용체 3은 비린 향기를 내는 분자와 결합하고, 수용체 1과 수용체 2는 풀 향기를 내는 분자와 주로 결합하네요! [행렬 2]는 강물, 나무, 꽃밭 냄새에 비린 향과 풀 향이 얼마나 들어 있는지를 나타내요.

행렬을 분해하면 숨은 특징이 쑤욱~!
어떤 행렬을 두 행렬의 곱으로 분해하는 건 수학자들의 아이디어예요.
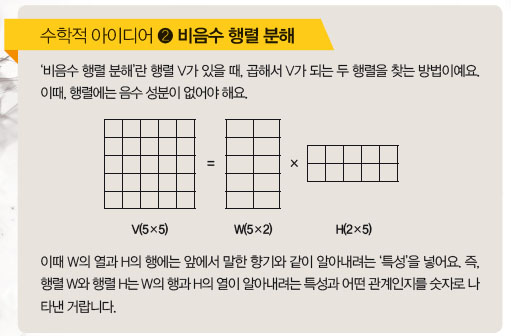
비음수 행렬 분해를 쓸 때 몇 가지 주의해야 할 점이 있어요. 우선 곱해서 처음 행렬이 되는 두 행렬을 찾을 때, 앞 행렬의 열의 개수와 뒷 행렬의 행의 개수를 실험으로 정해야 해요. 둘째, 행렬의 열과 행의 개수가 많아지면 행렬을 곱할 때 계산량이 엄청나게 늘어나요. 이 부분만 극복하면 비음수 행렬 분해는 ‘향기’처럼 정보의 숨어 있는 특성을 알아내는 데 아주 효과적이랍니다!
최 순경 : 그렇구나! 어서 강력계에 냄새를 증명할 수 있다고 얘기해야겠어! 순경이라고 날 무시한 형사들의 코를 납작하게 해줄 수 있겠군!

얼굴인식과 기사 분류도 행렬로!
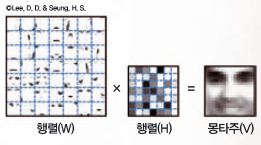
비음수 행렬 분해기법으로 조사대상의 숨겨진 특성을 분석할 수 있어요. 그래서 다양한 분야에 쓰이고 있죠. 첫 번째는 얼굴인식이에요. 컴퓨터는 눈, 코, 입에 대한 정보만 갖고도 누구의 얼굴인지 찾아내요. 이 기법을 써서 눈, 코, 입 사진이 성분인 행렬(W)과 어떤 행렬(H)을 곱해야 완전한 몽타주(V)가 나오는지 찾을 수 있어요. 찾아낸 행렬(H)은 서로 다른 눈, 코, 입 사진을 어떻게 겹쳐야 하는지를 나타내요. 컴퓨터가 얼굴을 인식하는 원리, 참 쉽죠?
비음수 행렬 분해기법은 ‘텍스트마이닝’에서도 써요. 인터넷에는 숫자로 된 정보도 있지만 한글, PDF, 파워포인트 같은 복합 문서나 블로그, SNS처럼 일정한 형식이 없는 정보가 더 많죠? 문서 형태에 관계없이 글로 된 모든 정보를 0과 1로 바꾼 뒤 유용한 정보만 뽑아내는 것이 텍스트마이닝 기술이에요. 빅 데이터 같은 대규모의 문서에 숨겨진 단어 사이의 연관성을 찾아 줘요.
예를 들어, 한 대형 마트는 텍스트마이닝 기술로 블로그, SNS를 분석해 기저귀를 사러 온 아빠들이 맥주도 함께 산다는 것을 알아냈어요. 그래서 맥주와 기저귀를 가까운 곳에 진열해 매출을 올렸대요. 텍스트마이닝 기술로 거리가 멀어 보이는 두 단어의 연관성을 밝힌 덕분이죠. 비음수 행렬 분해는 단어의 출현 빈도, 다른 단어와 동시에 출현하는 빈도와 같은 정보를 토대로 숨은 정보를 찾아낸답니다. 이 기법은 단어를 입력해 비슷한 주제의 기사나 글을 골라내는 데도 쓸 수 있어요.
비음수 행렬 분해기법에 대한 초기 연구 논문은 1994년 핀란드 헬싱키대 컴퓨터과학과 연구팀이 발표했어요. 하지만 당시 이 기법은 과정이 복잡해 실제로 연구에 응용하기 어려웠어요. 그러나 한국계 미국인인 세바스찬 승 미국 매사추세츠공대 교수와 다니엘 리 미국 펜실베이니아대 교수가 비음수 행렬 분해를 쉽게 하는 방법을 개발함으로써 이 기법이 더 널리 쓰이게 됐다는군요.
오초림 : 최 순경님, 이제 문제를 해결해 드렸으니 어서 만담 준비를 해야죠? 지금 강가로 수색하러 가신다고요? 그럼 연습은 언제 해요?! 저 극단에서 잘리면 안되는데에~!