
제1코스 기념일과 관계가 깊은 14
매달 14일에는 발렌타인데이, 화이트데이를 비롯해 다이어리데이(1월), 로즈데이(5월), 포토데이(9월) 등 각종 기념일이 있다. 그런데 왜 하필이면 14일에 이런 기념일들이 자리잡게 된 걸까?
발렌타인데이에서 그 이유를 찾을 수 있다. 발렌타인데이는 3세기 경 로마 시대의 성인 발렌티노(Valentinus)의 축일에서 유래됐다. 당시 로마 황제는 군대의 기강을 바로잡기 위해 황제의 허락 없이 젊은 병사들이 결혼을 할 수 없도록 명령을 내렸다. 하지만 로마 교회의 사제였던 발렌티노는 이 명령을 어기고, 서로 사랑하는 남녀의 결혼을 허락한 죄로 2월 14일에 순교했다고 전해진다. 이후 발렌티노를 기념해 2월 14일마다 연인들끼리 사랑을 고백하거나 선물을 주고받는 풍습이 생겨났다고 한다. 발렌티노의 영어식 표현을 따서 만든 것이 바로 발렌타인데이다.
그런데 1950년대 일본의 유명 제과 회사에서 ‘발렌타인데이에는 여자가 남자에게 초콜릿으로 사랑을 고백하라’는 캠페인을 시작했다. 이것이 널리 퍼져서 발렌타인데이에 여자가 남자에게 초콜릿을 선물하게 된 것이다. 또한 같은 회사에서 3월 14일에는 사탕을 주는 캠페인을 벌인 결과 화이트데이가 자리잡았다. 화이트데이는 일본, 대만, 한국 등 일부 지역에서만 행해지고 있는 기념일이다. 기념일을 이용하는 이러한 상업적 전략이 계속되며, 특히 우리나라에서 매달 14일마다 장미꽃이나 다이어리 등의 선물을 주고받는 기념일이 계속 만들어졌다.
하지만 3월 14일은 화이트데이인 동시에 파이데이다. 파이데이는 수학자들이 원의 지름에 대한 원둘레의 길이의 비인 원주율를 기념하기 위해 만든 날이다. 미국과 유럽을 중심으로 수학에 관심이 있는 사람들이 주축이 돼 각종 행사를 마련하고 있으며, 우리나라에서도 고등과학원에서 매해 파이데이 행사를 열고 있다. 원주율의 근삿값 3.14159…를 기념하기 위해 3월 14일 1시 59분에 맛있는 파이를 나누어 먹기도 하고, 원주율의 근삿값 외우기나 원주율과 관련된 글짓기 대회 등을 열기도 한다.
제2코스 π의 근삿값, 3.14는 어떻게 나왔나?

약 3.14라는 것을 알아 낸 것은 매우 오래 전 일이다. 기원전 3세기경의 수학자 아르키메데스도 알고 있을 정도였다. 지금은 슈퍼컴퓨터를 이용해 소수점 이하 수백만 번째 자리까지도 쉽게 알 수 있지만, 아르키메데스는 어떻게 π 값을 알아 낸 것일까?
바로 원에 내접하는 정다각형과 외접하는 정다각형을 이용한 방법 덕분이었다. 반지름의 길이가 r인 원의 둘레의 길이는 원에 내접하는 정다각형의 둘레의 길이보다는 크고, 원에 외접하는 정다각형의 둘레의 길이보다는 작다. 이 정다각형을 정n각형이라고 하면, n값이 커질수록 원의 둘레의 길이의 범위를 좀 더 정확하게 구할 수 있다.
30°, 45°, 60°와 같이 특수각에 대한 삼각비를 적절히 이용하면, 정삼각형, 정사각형, 정육각형의 변의 길이를 원의 반지름 r에 관해 나타낼 수 있다. 이를 통해 대략적인 π 값의 범위를 알아내 보자.
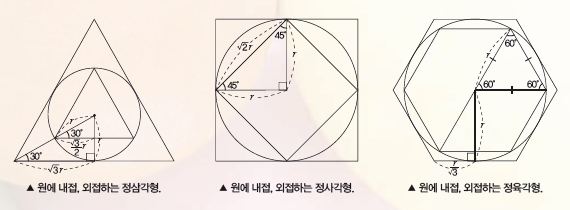


이 3개의 도형만 살펴봐도 정n각형의 n값이 커질수록 π 값의 범위를 더 정확하게 구할 수 있다는 사실을 확인할 수 있다. 아르키메데스는 이 아이디어를 가지고 원과 원에 내접, 외접하는 정96각형을 이용해 원주율의 근삿값이 대략 3.14라는 것을 알아냈다.

그런데 왜 하필 정96각형이었을까? 그것은 96=6×2⁴인 것과 관련이 있다. 왼쪽 그림과 같이 원에 내접하는 정육각형을 이용하면, 변의 개수가 2배인 원에 내접하는 정십이각형을 편리하게 만들 수 있다. 원에 외접하는 정육각형과 정십이각형의 경우도 마찬가지다.
따라서 아르키메데스는 이와 같이 정육각형을 기준으로 변의 개수를 2배로 늘리는 방법을 4번 반복해 정96각형을 만들었다. 그리고 여기서 얻은 원주율의 범위로부터 소수 둘째 자리까지 정확한 원주율의 근삿값 3.14를 구한 것이다. 지금으로부터 2000년도 훨씬 넘는 시대에 원주율의 근삿값을 얻어낸 아르키메데스의 내공은 정말 놀랍다.

제3코스 육각형과 경로의 수를 연결하는, 4번째 카탈란 수 14
육각형을 4개의 삼각형으로 나누는 방법에는 몇 가지가 있을까? 육각형을 4개의 삼각형으로 나누는 방법은 ‘4개의 삼각형들이 모두 한 꼭짓점을 지나는 경우(6개)+3개의 대각선을 사용하는 경우(6개)+정육각형의 가운데에 삼각형이 자리 잡는 경우(2개)’로, 모두 14가지다. 그림을 직접 그려 답을 확인해 보자.
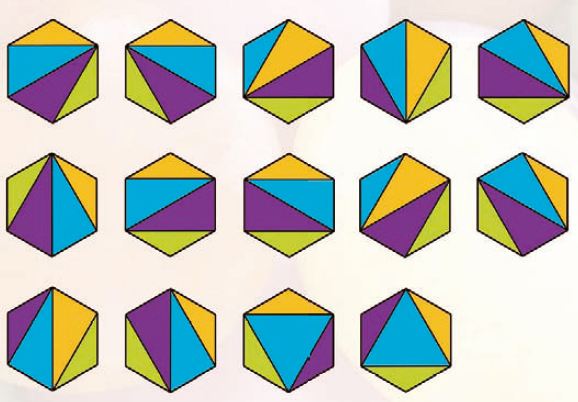
이 문제는 단순해 보이지만 사실 꽤 오랜 역사를 갖고 있다. 18세기 초 스위스의 수학자 레온하르트 오일러는 “n+2각형을 서로 교차하지 않게 대각선을 그어서 n개의 삼각형으로 나눌 수 있는 방법의 수는 몇 개인가?”란 질문을 던졌다. 오일러에 의해 발견된 몇 개의 수는 다음과 같다.

이후 벨기에의 수학자 카탈란이 오일러의 문제를 해결하면서 위 조건을 만족하는 수를 ‘카탈란 수’라고 부르게 됐다. 카탈란 수는 도형을 나누는 오일러의 질문에서 출발했지만, 경로의 수로도 소개된다. 좌표평면에서의 카탈란 수는 원점 (0,0)에서 출발해 (n,n)까지 가는 최단 경로 중, 직선 y=x의 그래프 위를 지나지 않는다는 조건을 만족해야 한다. 그럼 (0,0)에서 출발해 (4,4)까지 도착하는 4번째 카탈란 수를 직접 구해 보자.
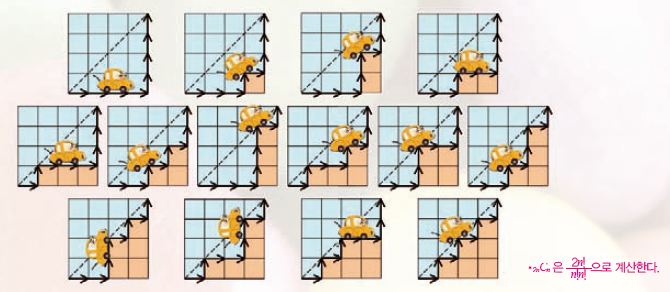
조건을 만족하는 경로의 수는 모두 14개다. 카탈란은 이를 다음과 같은 수식으로 나타냈다.

지금까지 살펴본 숫자 14의 다양한 면모 중 특히 기억에 남는 부분은 어떤 것일까? 발렌타인데이나 파이데이의 14일 수도 있고, 어떤 자연수의 제곱근의 근삿값을 구하는 과정이 흥미로웠을 수도 있다. 또 경우의 수에 관심이 많다면 4번째 카탈란 수인 14가 기억에 남을 수도 있다. 이제 기사에서 그치지 말고 인터넷이나 책을 통해 더 깊이 알아보도록 하자. 이 과정을 통해 숫자 14의 비밀을 더 알게 되는 기쁨을 누릴 수 있다. 그리고 그런 반짝이는 마음이 수학의 달인으로 가는 첫걸음이 될 것이다.











