
숫자 3에는 ‘완성’이라는 의미가 담겨 있다. 빛의 삼원색(빨강, 초록, 파랑)과 색의 삼원색(빨강, 파랑, 노랑)을 비롯해, 물체의 상태(고체, 액체, 기체)와 기독교의 삼위일체(성부, 성자, 성령), 불교의 삼보(불, 법, 승) 등 숫자 3에 들어 있는 완성의 의미는 무수히 많다. 또한 숫자 3은 캠페인에서도 인기가 있다. 각종 건강 관리와 마케팅 전략에서 333법칙은 기억하기에 좋아 활발히 쓰인다. 수학 속 숫자 3의 활약상을 살펴보자.
제1코스 우리가 사는 세상은 3차원!
최근 3D 영화나 3D TV가 인기를 끌고 있다. 여기서 3D란 ‘3D CG’, 즉 3차원 컴퓨터 그래픽(3-dimensional computer graphics)을 의미한다. 3차원 입체공간을 2차원 평면에 투영해 표현하는 3차원 컴퓨터 그래픽을 간단히 3D라고 부르는 것이다.
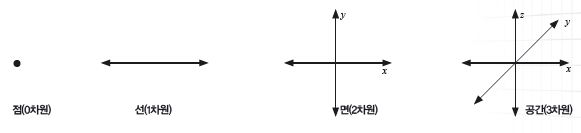
그럼 3차원(3D, 3 dimension)이란 무엇일까? 초등학교 때 배우는 수직선은 1개의 축으로 이루어졌으므로 1차원, 중학교 때 배우는 좌표평면은 x축과 y축, 2개의 축으로 이루어졌으므로 2차원으로 볼 수 있다. 여기에 축을 하나 더 추가해 x, y, z의 3개의 축으로 이루어진 공간이 바로 3차원이다. 우리가 살고 있는 세상이 바로 3차원 공간이며, 만약 우리가 마법에 의해 벽에 걸린 그림 속으로 빨려 들어간다면, 2차원 세상에 살게 되는 것이다.
제2코스 갑자기 사라진 UFO의 비밀은?
점, 선, 면, 공간에 해당하는 0, 1, 2, 3차원 세상에 진드기, 개미, 거미, 파리가 살고 있다고 생각해 보자. 진드기는 0차원, 즉 점 하나로 이루어진 세상에 살고 있다. 세상이 오직 점 하나뿐이므로 전혀 움직일 수 없고, 자신이 세계인 동시에 세계가 바로 자기 자신이다.
1차원의 개미는 선분과 같은 존재로, 선 위만 움직일 수 있다. 선을 따라 전진, 후진만 할 뿐이다. 개미는 선 외에 세상은 보이지 않기 때문에 다른 세상은 상상도 못할 것이다.
이제 1차원인 선 근처에 0차원인 점이 위치했다고 생각해 보자. 아무리 가까워져도 두 세상은 여전히 떨어져 있으므로 진드기와 개미는 서로를 알아차리지 못한다. 그러던 어느 날, 점이 선 위에 위치하게 된다. 이제 개미는 갑자기 등장한 진드기를 보고 퉁명스레 말한다.
“넌, 뭐야? 왜 길을 막고 있어? 저리 비켜~!”
하지만 진드기에게 점 바깥에 있는 개미는 보이지 않는다. 개미는 앞으로 나아가려면 진드기를 밀면서 갈 수밖에 없다. 뛰어넘으면 좋겠지만, 안타깝게도 1차원 개미는 뛰어넘는다는 개념을 갖고 있지 않다.
이번엔 2차원 평면에 사는 거미를 생각해 보자. 거미는 전후좌우 좌표평면 위 어디로든 자유롭게 이동할 수 있다. 하지만 높이가 없어 점프를 하거나 땅 속으로 기어들어갈 수는 없다. 평면 위에 개미가 살고 있는 선이 놓이면 어떻게 될까? 거미는 앞뒤로 왔다갔다만 하는 개미를 보고는 답답해서 말을 건다.
“어디 아파? 왜 자꾸 왔다갔다만 하니?”
하지만 1차원의 개미에게 거미는 보이지 않고 환청만 들릴 뿐이다. 답답해진 거미는 개미의 세상인 선 위로 가서 개미의 앞을 가로막는다. 그제야 개미가 깜짝 놀라며 말한다.
“뭐야? 넌 누군데 불쑥 나타난 거야?”
개미의 반응이 신기했던 거미는 한 걸음 물러서서 개미가 살고 있는 선에서 나온다. 그러자 개미는 안도의 숨을 내쉬며 말한다.
“어휴~, 내가 헛것을 봤나 보다.”
한편, 3차원 공간의 파리는 전후좌우뿐만 아니라 위아래로도 이동할 수 있다. 또한 3차원 공간에 있는 모든 존재를 인식할 수 있다. 이런 파리에게 0차원의 진드기나 1차원의 개미, 2차원의 거미는 모두 이상해 보일 뿐이다. 파리는 거미 근처로 날아가 말을 시켰다.
“거미야, 뭐 해?”
거미는 아무것도 보이지 않아 두리번거렸다. 파리는 이 모습이 답답해서 평면에 내려 앉아 다시 말했다.
“야! 내 말 안 들려?”
거미는 그제서야 파리를 발견하고는 파리에게 거미줄을 던졌다. 하지만 파리는 거미줄을 사뿐히 피하며 날아올랐다. 다시 파리를 보지 못하게 된 거미는 파리가 갑자기 없어졌다고 생각하며 굶주린 배를 아쉽게 쓰다듬는다.
이처럼 낮은 차원의 생물에게는 높은 차원의 생물이 갑자기 나타났다 사라지는 것처럼 보일 수 있다. 이런 현상을 통해 ‘UFO가 갑자기 나타났다 사라졌다’는 목격담을 설명할 수 있다. 예를 들어 3차원 이상의 시간축까지 있는 고차원의 외계인이 현재에서 미래로 이동하다가 우리 눈에 띄면 UFO가 나타났다 사라지는 것처럼 보일 수 있다.
차원 간 현상은 그밖에도 다양하고 재미있는 상황을 만들어 낼 수 있다. 이를 소재로 한 영국 애드윈 애보트의 1884년 소설 ‘플랫랜드(flat land)’는 이후 여러 소설에 영감을 주었고, 다양한 애니메이션의 소재가 됐다.
제3코스 3등분을 반복해 눈송이를 만들어라
프랙탈 도형에서도 3의 의미를 찾을 수 있다. 프랙탈 도형은 아무리 확대해도 자신을 1/a로 축소한 닮은 도형이 계속해서 나타나는 도형으로, 들쭉날쭉한 주름이 특징이다. 프랙탈의 대표적인 예로는 스웨덴의 수학자 로베르트 코흐가 소개한 ‘코흐의 눈송이 곡선’이 있다. 이 코흐의 눈송이를 얻기 위해서는 숫자 3과 무한반복이라는 인내심이 필요하다.
코흐의 눈송이를 만들려면 정삼각형의 각 변을 3등분한 뒤, 한 변의 길이가 처음 정삼각형의 ⅓에 해당하는 정삼각형을 아래 그림과 같이 붙여야 한다. 그 결과 얻은 각 변에 대해서도 이 과정을 계속해서 반복하면 코흐의 눈송이가 만들어진다.
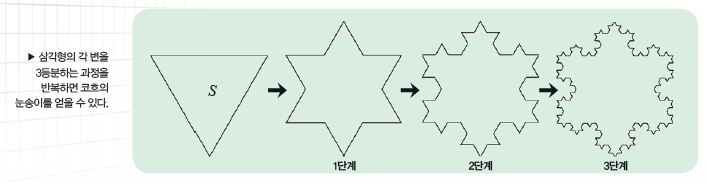

코흐의 눈송이 둘레의 길이는 각 단계마다 4/3배씩 늘어나기 때문에, 처음 정삼각형의 둘레의 길이를 ℓ이라고 하면 n번째 단계에서 코흐의 눈송이 둘레의 길이는 (4/3)ⁿℓ이 된다.
즉, n이 커짐에 따라 코흐의 눈송이 둘레의 길이가 무한히 커지는 것이다. 이처럼 코흐의 눈송이는 원래 정삼각형 넓이의 2배도 안 되는 넓이를 차지하면서, 그 둘레의 길이는 무한한 신비로운 도형이다.
이와 비슷한 예는 지도상에서도 찾아볼 수 있다. 바로 노르웨이의 해안선이다. 이 곳은 코흐 곡선처럼 굴곡이 심한 해안선 때문에 좁은 국토 면적에 비해 1만 8000km라는 긴 해안선을 가지고 있다. 또한 미국 알래스카 주의 해안선 역시 그 길이가 미국 나머지 주의 해안선 길이를 모두 합친 것과 거의 같을 정도로 매우 길다.
숫자 3은 우리가 살고 있는 3차원 세상뿐만 아니라, 자연에서 쉽게 발견되는 프랙탈 구조 등 다양한 곳에서 찾을 수 있다. 3월에는 숫자 3의 남은 매력을 모두 찾아보는 재미에 푹 빠져 보는 것은 어떨까?











