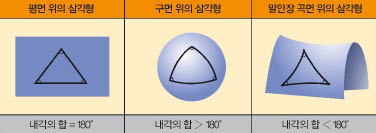
“박사님, 놀이공원에 와서 너무 좋아요! 저기 멀리 보이는 동그란 구조물은 가까이 보니까 삼각형으로 이뤄져 있네요.” “이 놀이공원의 상징인 ‘지구별’이란 이름의 구조물이란다. 겉이 삼각형으로 채워진 구조물이지. 그래서 삼각형에 관한 미션을 준비했단다.”
삼각형의 세 내각의 합은?
삼각형의 세 내각의 합은 180°다. 누구나 아는 사실이지만 이 사실이 진짜임을 보이려면 증명을 해야 한다. 삼각형은 세 점과 세 선분으로 이뤄져 있다. 예를 들어 평면 위의 서로 다른 위치에 점A, B, C를 표시한 다음, 세 점을 곧게 이으면 그림 ①과 같이 삼각형 ABC가 된다. 여기에 그림 ②에서처럼 꼭짓점 A를 지나고 변 BC에 평행한 선분 HG를 그리자. 엇각의 성질에 의해 ∠ABC와∠HAB가 같고, ∠BCA와 ∠GAC가 같다. 따라서 삼각형 ABC의 세 각의 합은 x+y+z=180°다.
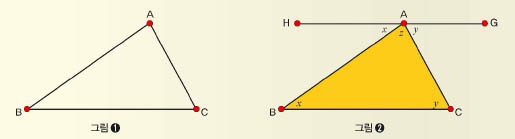
그런데 만약 삼각형의 세 변이 곡선으로 이뤄져 있다면 세 내각의 합은 어떻게 될까? 편의상 곡선으로 만들어진 삼각형을 ‘곡선 삼각형’이라 부르고, 직선의 일부인 선분으로 이뤄진 삼각형은‘직선 삼각형’이라 부르기로 하자.
평면에서 곡선 삼각형을 만들려면 컴퍼스를 이용해 크기가 같은 원 세 개를 겹치거나 접하도록 그리면 된다. 그림 ③은 크기가 같은 원 세 개를 겹쳐 그린 경우다. 원의 일부로 이뤄진 볼록한 곡선 삼각형 ABC가 생긴다. 반면 그림 ④와 같이 크기가 같은 원 세 개를 외접시키면 오목한 곡선 삼각형 ABC가 생긴다.
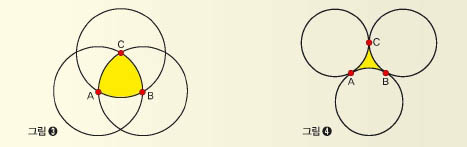
직선 삼각형과 비교해 보면 볼록한 곡선 삼각형의 세 내각의 합은 180°보다 크고, 오목한 곡선삼각형의 세 내각의 합은 180°보다 작다는 것을 알 수 있다. 이제 직선 삼각형의 세 내각의 합이 180°가 된다는 사실을 간단한 색종이 실험으로 확인해 보자.

지구의 어느 한 점에서 곰이 남쪽으로 이동하고 다시 서쪽으로 이동한 다음, 북쪽으로 이동했다.
그런데 도착 지점이 처음 출발한 곳이다. 어떻게 된 걸까?
이 문제를 풀려면 지구를 구라고 가정하고, 곰이 이동한 경로를 생각하면 된다. 곰은 직선으로 이동했고 방향을 두 번 바꿨는데, 처음 출발한 위치로 돌아왔으므로 곰이 이동한 경로는 지구 위에 그린 삼각형이다. 그런데 평면이 아니라 구 위에 그렸기 때문에 이 삼각형은 평면에 그린 삼각형과 다르다.
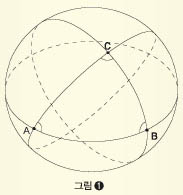
이와 같이 구면 위에 그린 삼각형을 ‘구면 삼각형’이라고 부른다. 구면 삼각형은 볼록한 곡선으로 이뤄져 평면 삼각형과 모양이 다르고, 세 내각의 합도 180°보다 크다. 그림 ①에서 점 A, B, C로 이뤄진 삼각형이 바로 구면 삼각형이다.
만약 곰이 평면에서 움직였다면 곰의 이동경로는 ‘ㄷ’자 모양이 되므로 만날 수 없다. 그러나 구 위에서 움직이면 이동경로가 삼각형이 될 수 있다. 특히 곰이 지구 위에서 직선으로 이동하다가 90°씩 두 번 방향을 바꿨기 때문에 곰의 이동경로는 세 각이 모두 90°인 삼각형이다! 그런데 모든 각이 90°인 삼각형이 되려면 삼각형의 꼭짓점은 반드시 극점과 적도에 있어야 한다. 따라서 곰은 북극에서 출발했다는 얘기다.
한편 구면 위에 그린 삼각형이 볼록한 삼각형이라면, 오목한 면 위에 그린 오목 삼각형도 있다. 오목한 삼각형을 그리려면 말안장 모양처럼 생긴 곡면위에 삼각형을 그리면 된다. 말안장 곡면 위에 그린 이 삼각형의 내각의 합은 180°보다 작다. 따라서 공간을 평면, 볼록한 면, 오목한 면으로 나누면 각각의 경우마다 서로 다른 삼각형이 생기고, 내각의 합도 달라진다는 점을 알 수 있다.