d라이브러리

이번 호에서는‘방정식’에 대해 꼼꼼히 살펴보겠습니다. 방정식에 대한 처방전은 서울 보성여자중학교로 찾아가 박광순 선생님께 받아왔습니다. 오늘 도움 말씀을 주실 보성여중 박광순 선생님은 올해로 보성여중 학생들과 함께하신 지 8년째를 맞고, 2009년부터 서울 중부교육청 영재교육원에서 수학영재를 지도하고 계십니다. 또 2009년부터 전국수학교사모임‘교실 관찰팀’에서 활동해왔는데, 현재는 팀장도 맡고 계시죠. 2010년에는 7월 27일 방영된 KBS 시사기획‘떠들썩 교실, 수업을 바꾼다’에 출연하기도 하셨어요. 보성여중에는 학교도서관에 수학동아가 비치돼 있을 정도로, 수학동아를 사랑하는 학생들이 많았어요. 오늘은 특별히 박광순 선생님의 수업을 듣는 보성여중 1학년, 3학년 학생들과 함께했습니다.


선생님, 궁금합니다!
선생님, ‘방정식’은 왜 공부하나요?

방정식은 여러분이 상상하는 것보다 훨씬 많이 생활 속에서 쓰이고 있는데, 사실 일상생활 속에서 발생하는 문제를 풀기 위해 발전했죠. 예로부터 실생활 문제를 해결하기 위해 방정식이 이용됐다는 기록이 있어요. 방정식은 중국에서 가장 오래됐다는 약 2000년 전의 수학 책‘구장산술’에 전해 내려오고 있어요. 구장산술은 총 9장으로 나뉘어 있는데, 그중 제8장의‘방정(方程)’에는 1차 연립방정식의 계산문제를 가감법으로 푸는 방법이 나오고, 제9장의‘구고(句股)’에는 직각삼각형에 관한 문제로 피타고라스 정리를 이용한 응용문제와 2차 방정식 문제가 나오죠. 예를 들어 설명할게요.

구장산술 제8장‘방정’의 제1문제

"지난해 우리 논에서는 상품 1뭇(단), 중품 2뭇, 하품 3뭇에서 26말의 쌀이 나왔는데 너희 논에서는 몇 말씩의 쌀이 나왔는지 기억하니?" 셈돌이가 묻자 지난해, 쇠돌이네 논에서는 상품 3뭇, 중품 2뭇,하품 1뭇에서 39말의 쌀이 나오고, 개동이네 논에서는 상품 2뭇, 중품 3뭇, 하품 1뭇에서 34말의 쌀이 나왔다고 쇠돌이와 개동이가 대답했다. "그러면 우선 하품 1뭇에서 몇 말의 쌀이 나오는지 계산해보자. 음…,2.75말의 쌀이 나오겠네."
*여기서 1말=18039ml=18.039L

이 문제를 우리가 배우는 방정식에 빗대어 생각해보면 상품은 x, 중품은 y, 하품은 z라 둘 수 있습니다. 미지수가 3개이고 식이 3개인 방정식을 세워 문제를 해결할 수 있겠죠. 하지만 구장산술에서는이 문제를 *산가지를 이용해 풀었어요.
 

오른쪽 표와 같은 방법으로 *산가지를 놓아 방정식을 풀었는데, 산가지를 늘어놓은 모양이 정사각형(정방형) 또는 직사각형(장방형)을 이루었다고 해서 네모 모양을 뜻하는 방(方), 나눈다는 뜻의 정(程)으로 구성된‘방정’이라는 말이 생겨났다고 해요. 방정식은 여기서 유래된 거죠.

이처럼 실생활의 문제를 해결하기 위해 유래된 방정식은 초등학교 6학년 때부터 고등학교에 이르기까지 단계적으로 공부합니다. 따라서 어느 한 부분의 개념을 놓치면 크게 고생할 수 있으니 처음 배울 때, 개념을 정확히 알고 넘어가야 합니다.

*산가지: 예전에 셈하는 데 쓰던 막대기를 말한다. 일, 백, 만 단위는 세로로 놓고, 십, 천, 억(지금의 십만) 단위는 가로로 놓아 수를 표시했다.


한 걸음 더

올해부터는 초등학교 6학년 때부터 간단한‘방정식’단원을 공부합니다. 이전에는 미지수를 □로 표시했는데, 이제는 초등학교 때부터 도형 대신 문자로 나타내는 연습을 하는 거죠. 방정식을 처음 접할 때는 문자나 미지수, 변수의 개념을 정확히 이해하고 문제를 풀어야 합니다. 자칫 잘못하면 방정식의 개념을 정확히 모르고 단순히 미지수를 구하는 방법만 외우는 학생이 생길 수 있거든요. 초등학교 때는 먼저 방정식과 관련된 생활 속 상황을 충분히 접하고, 그 상황을 어떻게 해결할지에 집중하는 것을 추천합니다.



선생님만 알고 있는 비밀
선생님, 학생들이 방정식 문제를 풀 때 어떤 실수를 자주 하나요?

객관식으로 출제된 문제를 해결할 때는 별 무리가 없지만 서술형 문제를 풀 때 학생들이 많이 하는 실수를 알아볼게요. 여러분도 아래의 두 풀이과정을 비교해 보고 잘못된 부분을 찾아보세요.
 

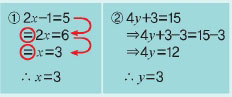
두 풀이는 어떤 차이점이 있나요? 풀이에 ‘등호(=)’와‘화살표(⇒)’를 각각 다르게 사용한 점이 보이나요? 둘 중 한 사람은 잘못된 기호를 사용했어요.

찾았나요? 맞습니다, 학생들이 서술형으로 풀이를 쓸 때, 무심코 많이 하는 실수 중의 하나가 등호(=)의 남용이에요. 등호(=)를 사용할 때는 등호를 기준으로 등호가 성립하는지 반드시 확인해야합니다. 예를 들어, ①번의 풀이대로라면, 5=6=3 이라는 오류가 생기거든요. ②번의 풀이와 같이 행을 바꿔 풀이를 이어나갈 때는 등호(=)대신 화살표(⇒)를 사용하거나 화살표(⇒)를 생략하는 것이 올바른 풀이방법이랍니다.

②번 풀이에서 조금 아쉬운 점이 있다면 등식의 성질을 이용해 풀이과정을 써 내려갔으니, 마지막 4y=12에서 양변에 $\frac{1}{4}$을 곱하거나, 4를 나눠 답을 구하는 과정을 썼다면 더 좋을 뻔했네요.


보성여중 학생들의 생 생 노하우

기자는 보성여자중학교 3학년 7반 교실에서 수학동아를 즐겨 보고 있다는 1학년, 3학년 학생 8명을 만날 수 있었어요. 평소 수학 공부에 관심이 많아서 늘 수학시간이 기다려진다는 학생들이에요.

오늘의 주제가‘방정식’인 만큼 학생들이‘방정식’을 배우고 시험을 보는 동안 어려웠던 점과, 실수를 최소한 줄일 수 있는 노하우를 물어봤어요.

1학년 대표로 김윤지 학생은 자신의 어려움과 노하우를 소개해주었답니다.“저는 객관식 문제를 풀때보다는, 서술형 문제를 풀 때 어려움을 겪는 것 같아요. 평소에 서술형 문제나 고난도 문제를 풀 때 포기하지 않고 절대 답지를 보지 않으며 문제를 푸는 연습을 해요. 답지를 보기 시작하면 문제에 대한 흥미가 떨어지거든요. 한 문제를 풀더라도 스스로 풀 수 있는 데까지 풀어보는 끈기가 수학과목에서 중요한 것 같아요.”

또한 3학년 7반 학급회장을 맡고 있는 구주현 학생은 ‘연속한 세 자연수의 합이 102일 때, 자연수 중 가장 큰 수를 구하라’와 같은 활용 문제를 예로 들어 설명해주었어요.“이 문제는 미지수 x로 놓는 값과 구하고자 하는 값이 달라 조심해야 하는 문제예요. 연속한 세 자연수의 합이 조건으로 제시 됐으니, 각각을 x-1, x, x+1로 생각해야 합을 식으로 세울 때 간단하게 3x가 돼 계산이 쉽거든요. 하지만 문제에서 요구하는 답은 가장 큰 수니 x 값을 그대로 정답으로 썼다간 다 구해놓고 틀리게 되죠.방정식 활용문제를 풀 때는 항상 미지수 x와 문제에서 요구하는 답이 같은 값인지 반드시 확인하는 습관이 중요한 것 같아요.”


박광순 선생님의 ‘방정식’ 정복 비법 전수!

방정식 문제를 비롯한 수학 문제를 풀 때, 문제의 답에 관심을 갖기보다 그 풀이과정에 관심을 갖도록 노력해야 합니다. 그래야 문제 해결력을 키울 수 있어요.

특별히 방정식은 실수 없이 식을 풀어내야 하는 어려움도 있지만, 활용문제에서는 식 세우기가 가장중요하죠. 이때 포기하지 않고 스스로 해결할 수 있는 부분까지 꾸준히 도전하는 습관이 중요해요. 설사 답이 틀렸더라도, 풀이과정을 고민하고 써 내려가면서 배우는 점이 분명히 있거든요.

혹시 수학에 흥미가 떨어지고 있는 단계라면, 무엇보다 수학을 가까이 하려는 자신만의 의지가 중요합니다. 의지가 생기면 교육방송의 EBSi 동영상프로그램이나, 재미있는 수학 교양 서적 등을 통해 수학의 매력을 발견할 수 있어요. 아! 서울교육연구정보원의 수학센터에 방문하는 것도 추천합니다.

마지막으로 제게‘수학’이란‘무한 질문’인 것 같아요. 학창시절에는‘이 문제는 왜 이렇게 풀지?’라는 물음을 끊임없이 제 자신에게 던졌다면, 수학교사가 된 지금은 ‘학생들은 왜 이 문제를 이렇게 풀지?’‘지금 이 상황에서 학생들은 어떤 수학적 사고를 하고 있지?’‘학생들에게 수학을 좀 더쉽게 잘 가르치려면?’ 등과 같은 무한한 질문을 쏟아내고 있어요. 여러분에게도 수학이 끊임없이 호기심과 궁금증을 일으키는 과목이 됐으면 해요.


도전! 나만의 수학문제 만들기

박광순 선생님은 수학 공부의 완성은 스스로 문제를 만들어 보는 것이라고 조언해 주셨어요. 다음 예시를 보고, 수학동아 독자 여러분도 나만의 수학문제를 만들어 보세요!
 

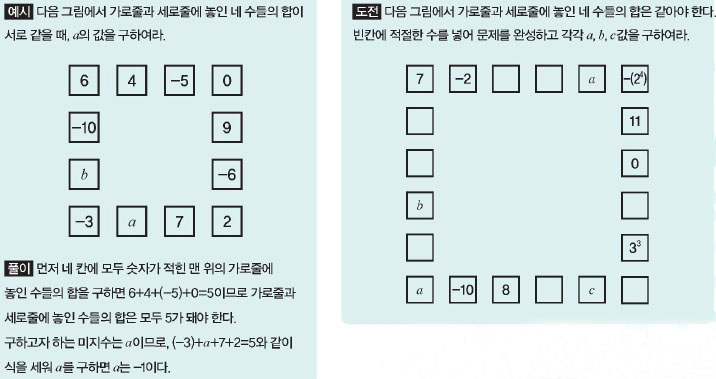
예시 
다음 그림에서 가로줄과 세로줄에 놓인 네 수들의 합이 서로 같을 때, a의 값을 구하여라.

풀이
먼저 네 칸에 모두 숫자가 적힌 맨 위의 가로줄에 놓인 수들의 합을 구하면 6+4+(-5)+0=5이므로가로줄과 세로줄에 놓인 수들의 합은 모두 5가 돼야 한다. 구하고자 하는 미지수는 a이므로, (-3)+a+7+2=5와 같이 식을 세워 a를 구하면 a는 -1이다.

도전
다음 그림에서 가로줄과 세로줄에 놓인 네 수들의 합은 같아야 한다. 빈칸에 적절한 수를 넣어 문제를 완성하고 각각 a, b, c값을 구하여라.