d라이브러리

중·고교 교과과정의 수학을 넘어서지 않는 수준에서 해결할 수 있는 재미있는 수학 연구 주제들을 소개하고 있습니다. 이번에는 매우 즐거운 주제인 타일 깔기 중에서 골라보았습니다. KAIST 사이버영재교육센터에서 2002년에 출제되었던 과제입니다.


1963년 소련 수학올림피아드에 다음과 같은 문제가 나온 적이 있다.

동기가 된 예제
 

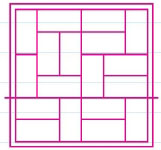
6×6 크기의 체스판에 2×1 크기의 도미노들을 서로 겹치지 않게 완전히 깔 때, 체스판의 한쪽 변에서 도미노들 사이의 경계로 이어진 금을 따라 반대쪽 변까지 닿는 직선이 반드시 적어도 하나 생김을증명하여라.

이 문제에서와 같이 한쪽 변에서 그 대변까지 타일들 사이의 경계를 따라 가로지를 수 있는 직선을 속선(fault-line)이라 하고, 속선이 하나도 생기지 않도록 타일을 까는 것을 속선 없이 타일깔기(fault-free tiling)이라고 한다.


증명
 

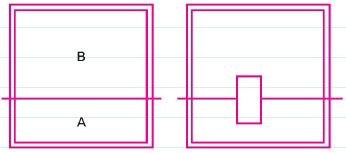
이 문제의 증명은 속선 없이 타일 깔기가 성공했다고 가정했을 때 모순을 찾아내는 귀류법을 사용한다. 즉, 다음과 같이 6×6 체스판의 임의의 가로선 혹은 세로선을 생각할 때, 이 선이 속선이 아니려면 이 선을 가로질러 깔리는 도미노가 적어도 하나 있을 것이다.

그런데, 만일 이 선 위를 가로지르는 도미노의 개수가 위와 같이 단 하나뿐이라면, A영역과 B영역의남은 넓이는 홀수가 되므로, 각각 따로 도미노로 겹치지 않게 완전하게 깔릴 수 없다.(도미노는 넓이가 2이므로, 도미노 몇 개로 깔리는 영역의 넓이는 짝수가 되어야 한다.)

따라서, 이 선 위를 가로지르는 도미노는 2개 이상 있어야 한다.

이것이 임의의 가로선과 임의의 세로선에 대해 다 그런 것이므로, ① 가로선: 5개 → 세로방향으로 깔리는 도미노: 적어도 10개, ② 세로선: 5개 →가로방향으로 깔리는 도미노: 적어도 10개 등, 속선을 없애기 위해 사용되는 도미노는 모두 적어도 20개가 있어야 한다.

그런데, 6×6 체스판의 넓이는 36이므로, 18개의 도미노로 가득 깔린다. 이것은 모순이므로, 속선 없이 타일 깔기는 불가능하다.

 

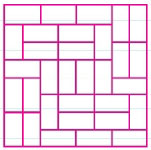
재미있는 증명이 아닐 수 없다. 홀짝에 대한 테스트만으로, 18과 20 이상으로 교묘하게 수가 어긋나서 증명에 성공하고 있다. 하지만, 사실은 이러한 증명이 성공되는 크기의 문제가 선택되어 출제된 것이다. 8×8에서 위와 같은 논리를 적용해보면, 여기에는 가로선이 7개, 세로선이 7개이므로 모두 (7+7)×2=28개 이상의 도미노를 써야 한다고 나온다. 넓이 64의 판에는 32개의 도미노가 쓰여야 하므로, 이것은 아무런 논리적 모순을 일으키지 않는다. 사실은 8×8 크기의 체스판에서는 2×1 크기의 도미노들로 속선 없이 타일 깔기를 할 수 있다. 이것 역시 같은 대회의 이어지는 문제였다.

그럼 이제는, 어떤 크기에서는 속선 없이 타일 깔기가 가능하고 또 어떤 크기에서는 불가능한지 그것을 알고 싶을 것이다. 우선 ‘속선 없이’의 조건이 없이, 도미노로 잘 깔리는 직사각형판의 조건부터 알아야겠다.


문제 1

2×1 도미노로 겹치지 않게 잘 깔 수 있는 m×n 크기의 체스판은 m 또는 n이 짝수인 것들임을 보여라.

이제 속선 없이 타일 깔기의 조건에 대해 연구해보자.


문제 2

m×n 크기의 체스판을 도미노로 속선 없이 까는 것이 가능하다면, m과 n 모두 5 이상임을 보여라. 단, 2×1의 체스판만은 논외로 한다.

이제 다음 크기의 체스판들에 대해 속선 없이 타일 깔기를 생각해보자. m×n이 짝수이므로, 일반성을 잃지 않고, 열의 수 m이 짝수라고 해도 되겠다. 또한, m과 n이 둘 다 짝수일 때에는, 일반성을 잃지 않고, m≤n이라 해도 되겠다. 즉, 우리는 다음의 크기인 경우들에 대해서만 판단해주면 된다.

(6+2m)×(5+2n), (6+2m)×(6+2n) (m, n≥0) 후자에서 6×6 크기는 불가능하고 8×8 크기는 가능함은 이미 앞에서 확인하였다.


문제 3

(1) 6×5 크기와 6×8 크기의 체스판은 도미노로 속선 없이 깔 수 있음을 보여라.
(2) (6+2m)×(5+2n) 크기나 (6+2m)×(8+2n) 크기의 체스판은 늘 도미노로 속선 없이 깔 수 있음을 보여라. 단, m, n은 0 이상의 정수이다.

정리
m×n 체스판 중에서 도미노로 속선 없이 깔 수 있는 경우는 2×1, (6+2m)×(5+2n)과 (6+2m)×(8+2n), 그리고 이들의 가로와 세로가 뒤바뀐 경우들이 전부이다. 단, m, n≥0

이것으로 도미노로 하는 속선 없이 타일 깔기에 관한 즐거운 연구를 마쳤다. 그런데, 이것을 3×1 크기의 타일로 까는 문제로 확장시켜도 즐거운 연구가 가능하다. 또한, 일반적으로 k×1 크기의 타일(k×1 빔)로 확장해도 역시 비슷한 결과를 얻을 수 있다.


문제 4
3×1 빔으로 m×n 체스판을 겹치지 않게 가득 깐다면 3|mn 임을 보여라. 단, a|b는 a가 b의 약수라는 표현이다.

일반적으로 k×1 빔으로 m×n 체스판을 깐다면, k|mn이라는 것도 위 문제의 결과로부터 쉽게 확장될것이다. 그러나,‘k|mn’이라고 해서 늘 타일이 잘 깔리는 것은 아니다.


문제 5

(1) 4×1 빔으로 6×6 체스판을 깔 수 없음을 보여라.
(2) k×1 빔으로 m×n 체스판을 깔려면, m 또는 n이 k의 배수가 되어야 함을 보여라.
이제 3×1 빔과 k×1 빔으로 속선 없이 타일을 깔 수 있는 크기를 찾아보자.


문제 6

(1) 3×1 빔으로 9×7 체스판을 속선 없이 깔 수 있음을 보여라.
(2) 2×1 도미노로 6×5 체스판을, 그리고 3×1 빔으로 9×7 체스판을 속선 없이 깔 수 있었음을 잘관찰하여, k×1 빔으로 속선 없이 깔 수 있는 체스판의 크기 m(k)×n(k)를 하나씩 찾아주어라. 단, m(k)≥n(k)
(3) 3×1 빔으로 9×8 과 9×9 체스판을 속선 없이 깔 수 있음을 보여라.


문제 7

3×1 빔으로 (9+3m)×(7+n) 크기의 체스판을 속선 없이 깔 수 있음을 보여라. 단, m과 n은 음이 아닌 정수.


문제 8

지금까지의 결과들을 잘 응용하고 더 연구하여, k×1 빔으로 속선 없이 깔 수 있는 m×n 체스판을 모두 찾아라.