d라이브러리

수에서 가장 기본이 되는 수는 자연수다. 그 다음은 0과 음수를 포함한 정수고, 정수를 포함한 더 큰 수는 유리수로 분수로 나타낼 수 있는 수를 말한다. 그렇다면 분수로 나타낼 수 없는 수는? 오래 전 피타고라스는 그의 제자와 ‘피타고라스정리’에 대해 이야기하면서 또 다른 수의 필요성을 느꼈다. 분수로 나타낼 수 없는 수, 즉 규칙 없이 끝없이 이어지는 소수인 ‘무리수’는 어떻게 발견된 것일까?


기원전 5세기경 그리스에서는 우주와 자연 현상에 대한 연구가 활발했다. 특히 피타고라스학파 사람들은 ‘만물은 수’라고 믿으며 우주의 모든 질서는 수로 표현할 수 있다고 생각했다. 그들에게 수는 매우 특별했고, 모든 수는 정수비(분수)로 표현할 수 있다고 믿었다. 예를 들어 피타고라스학파는 수에 의미를 부여했다. 모든 정수는 1을 더해서 만들 수 있으므로 1은 모든 수의 창조자로, 2는 첫 번째 짝수로 여성을, 3은 남성을, 4는 정의를, 5는 2와 3의 합이므로 결혼을 의미했다. 또 모든 도형의 선분의 비는 정수비로 이뤄졌다고 생각했다.

왼쪽 그림은 중세의 화가 라파엘로가 그린 ‘아테네 학당’ 모습이다. 왼쪽 아래에서 책에 무언가를 열심히 적고 있는 사람이 피타고라스다. 피타고라스 옆에 제자가 들고 있는 칠판을 살펴보자. 칠판의 문자를 점으로 나타내면 삼각형 모양으로 배열된다.

삼각형 모양으로 배열된 점의 개수는 위에서부터 차례로 1, 2, 3, 4 이고 삼각형 모양을 만들 수 있는 점의 개수는 1, 3, 6, 10임을 알 수 있다.
 

이와 같이 삼각형을 만들 수 있는 점의 개수인 1, 3, 6, 10… 과 같은 수를 ‘피타고라스의 삼각수’라고 한다. 피타고라스학파는 이처럼 수를 점으로 나타내 배열한 수에 관심이 많았다. 같은 원리로 ‘사각수’, ‘오각수’, ‘육각수’도 있다.

이제 피타고라스를 가장 유명하게 만든 ‘피타고라스의 정리’를 보자.

피타고라스 정리에서 가장 단순하면서도 아름다운 비는 3:4:5다. 이 때 빗변은 5, 나머지 두 변은 3과 4다. 그런데 직각을 낀 두 변의 길이가 각각 1일 경우 빗변은 유리수로 나타낼 수 없다. 결국 피타고라스는 새로운 수의 존재를 깨달았고 ‘무리수’가 탄생하게 된다. 이와 관련된 약 2500년 전의 피타고라스와 그의 제자 히파수스의 대화를 보자.

피타고라스 : 직각삼각형에서 직각을 낀 두 변의 길이가 각각 3, 4일 때 빗변은 얼마인가?

히파수스 : 3의 제곱과 4의 제곱의 합은 25입니다. 25는 5의 제곱이므로 빗변의 길이는 5입니다.

피타고라스 : 직각삼각형에서 직각을 낀 두 변의 길이가 각각 5, 12일 때 빗변은 얼마인가?

히파수스 : 5의 제곱과 12의 제곱의 합은 169입니다. 169는 13의 제곱이므로 빗변의 길이는 13입니다.

피타고라스 : 아주 잘했다. 질문이 있느냐?

히파수스 : 예. 직각을 낀 두 변의 길이가 1인 직각삼각형의 빗변의 길이는 얼마입니까?

피타고라스 : …….

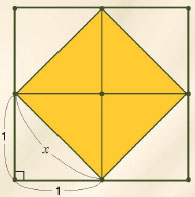
위의 대화에서 히파수스의 질문을 수학으로 표현해 보자. 한 변의 길이가 2인 정사각형을 네 개의 정사각형으로 나누자. 그런 뒤 큰 정사각형의 네 변의 중심을 선분으로 이으면 안에 또 다른 정사각형이 생긴다. 이 때 큰 정사각형의 넓이는 2×2=4가 되고, 작은 정사각형의 넓이는 큰 정사각형의 ${1}^{2}$이므로 2가 된다. 즉 큰 정사각형의 넓이는 작은 정사각형 넓이의 2배다.
 

그렇다면 히파수스 이전 시대의 사람들은 무리수를 몰랐던 것일까? 그렇지는 않다. 약 3600년 전 고대 바빌로니아의 점토판에서 무리수 계산에 대한 흔적을 볼 수 있다. 그 정확한 값을 수나 문자로 나타내진 못했지만 오늘 날의 계산으로 따져 봐도 놀라울 만큼 정밀한 근삿값을 사용하고 있었다.
 

대각선 부근의 숫자를 60진법을 이용해 소수로 나타내면 다음과 같다.
 

수학에서는 새로운 것을 발견하더라도 공식적으로 받아들이기까지는 오랜 시간이 걸리기도 한다. 왜냐하면 수학에서 어떤 개념을 받아들이기 위해서는 논리적인 증명이 뒷받침돼야 하기 때문이다. 고대 바빌로니아인들과 피타고라스가 오래 전 이미 ‘무리수’의 존재를 알았지만 19세기가 돼서야 무리수를 인정한 것처럼 말이다.
 

√는 라틴어로 뿌리(radix)를 뜻하는 단어의 머리글자 r이 변형된 것으로 1525년 크리스토프 루돌프가 처음 사용했다.

대표적인 무리수 π와 e
원주율 π: 원의 크기에 관계없이 원 둘레를 지름으로 나눈 값은 3.141592…으로 일정하고 그 값을 원주율이라고 한다. 순환하지 않는 무한소수기 때문에 근삿값 3.14로 쓴다.

자연상수 e : 근삿값은 약 2.7182이며 자연 및 사회 현상을 분석할 때 사용하는 수다.