d라이브러리

최근 인기를 끌고 있는 드라마 ‘선덕여왕’에서 미실은 월식을 정확히 예언함으로써 권력을 장악한다. 당시 백성들은 일식이나 월식과 같은 천문 현상을 하늘의 뜻으로 여겼기 때문에 민심을 움직이기 위해서는 천문 현상을 잘 예언할 수 있어야 했다.

미실이 월식을 예측하는 데 결정적인 역할을 한 ‘사다함의 매화’는 바로 역서, 즉 역법이 담긴 책으로 밝혀진다. 역법이란 해와 달, 별 등이 만들어 내는 천문 현상을 계산하고 예측하는 방법을 말한다. 오늘날과 같은 정교한 관측 도구나 컴퓨터도 없던 시절에 천문 현상은 어떻게 예측했을까?


하늘의 뜻, 일식

드라마 ‘선덕여왕’의 배경인 신라 시대에서 시간을 약 800년 뒤로 돌려 보자.

때는 세종이 즉위한 지 4년째 되던 1422년 1월 23일. 세종대왕과 신하들이 소복을 입고 제단에 올라 의식을 준비하고 있다. 다들 긴장한 표정으로 하늘을 바라보며 뭔가를 기다리는 중이다. 그런데 시간이 갈수록 세종대왕의 표정이 점점 일그러진다. 동시에 신하들의 얼굴에는 땀이 흐르고….

그 때 사람들의 입에서 탄성이 흘러나온다. 밝게 빛나던 해의 한 구석이 마치 누가 베어간 듯이 사라지기 시작한 것이다. 주위도 서서히 어두워지기 시작한다. 세종대왕은 의식을 치른 뒤 다시 햇빛이 나자 해를 향해 네 번 절을 한다.의식은 이렇게 무사히 끝나지만, 화가 난 세종대왕의 입에서 고함소리가 터져 나온다.

“일식을 잘못 계산한 관리에게 곤장을 쳐라~!”

전통 시대에 해는 왕을 상징했기 때문에 해가 가려지는 일식은 나라에 커다란 재앙이 닥친다는 것을 뜻했다. 그래서 예로부터 왕은 역법을 담당하는 관리를 두어 끊임없이 하늘을 관찰하면서 일식이 언제 일어나는지 계산하도록 했다.

우리나라의 일식 기록은 삼국 시대까지 거슬러 올라간다. 삼국사기에는 67번의 일식이 기록돼 있고, 고려 시대에는 일식이 137번 일어났다는 기록이 있다. 조선 시대에는 더 많아 총 261번의 일식이 기록돼 있다. 약 2년에 한 번씩 일식이 일어났다고 기록한 것이다.

조선 시대에는 일식이 일어나는 날짜를 계산해 두었다가 석 달 전에 나라 전체에 알렸다. 일식이 일어나는 날이면 왕과 신하들은 궁전 뜰에 모여 일식이 무사히 지나가기를 하늘에 빌었다. 그 날만은 백성들도 하루를 경건하게 보내야 했다. 음악을 연주하고 노래를 부르는 등 노는 일도 자제했다.

일식을 정확하게 예측할 수 있다는 것은 왕이 하늘의 뜻에 충실히 따르고 있다는 뜻이었다. 따라서 왕은 자신의 권위를 높이기 위해서 일식이 일어나는 시간을 정확히 예측하는 데 많은 노력을 기울였다. 이를 위해서는 최신 역서는 물론 역법을 계산할 수 있는 뛰어난 수학자가 매우 중요했다. 조선 시대에는 국가적으로 수학자를 길러 낸 뒤 가장 우수한 인재를 역법을 계산하는 관리로 임명했다.

미실이 역서인 ‘사다함의 매화’를 중요하게 여겼던 것이나, 세종대왕이 일식이 일어나는 시간을 잘못 계산한 관리에게 벌을 내린 것은 당연한 일이었다. 이렇듯 일식은 굉장히 중요한 천문 현상이었고, 그에 따라 일식을 계산하는 방법 또한 오래 전부터 알려져 있었다.


일식의 비밀은 황도와 백도의 기울기
 

일식을 계산하기 위해서는 일식이 왜 일어나는지 알아야 한다. 일식은 달이 해를 가리는 현상으로 지구-달-해의 순서로 나란히 놓일 때 일어난다. 그렇다면 달은 지구 주위를 한 달에 한 번 공전하니까 일식도 한 달에 한 번 일어나야 할 텐데, 왜 그렇지 않을까?

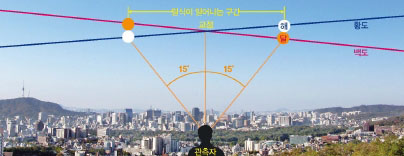
지구에서 바라볼 때 해가 지나가는 길을 황도, 달이 지나가는 길을 백도라고 한다. 황도와 백도가 완전히 똑같이 겹친다면 한 달에 한 번씩 개기일식이 일어난다. 하지만 황도와 백도는 서로 5° 기울어져 있기 때문에 대부분의 경우 해와 달은 위아래로 스쳐지나간다. 황도와 백도가 만나는 점을 교점이라고 하는데, 일식은 이 교점에서 일어난다. 해와 달이 동시에 교점 근처에서 만나는 순간이 바로 일식이 일어나는 순간이다.

해와 달, 그리고 교점 사이의 거리는 지구에서 각각 교점과 해 또는 달을 향해 직선을 그었을 때 두 직선 사이의 각도로 나타낸다. 일식이 일어나기 위해서는 해와 달이 만났을 때 교점으로부터의 거리가 15°보다 작아야 한다. 교점과의 거리가 15°보다 작은 곳에서 해와 달이 만나면 최소한 해의 일부가 가리는 부분일식이 일어난다. 교점과 가까워질수록 가리는 부분이 많아지고, 교점에서는 개기일식이 일어난다.

그러면 일식은 얼마나 자주 일어날까? 일식이 일어나려면 해와 달이 만날 때 교점으로부터의 거리가 15°보다 작아야 하므로 교점 앞뒤로 30° 범위에 있어야 한다. 해는 황도를 따라 1년에 360°를 돌기 때문에 30°를 움직이는 데는 약 한 달인 30~31일이 걸린다. 달이 지구를 한 바퀴 도는 데 한 달이 걸리므로 이 기간 동안 최소한 1번은 일식이 일어난다. 교점이 두 군데이므로 대략 6개월마다 1번씩, 즉 1년 중 일식이 최소한 2번은 일어난다는 뜻이다. 우리가 일식을 드물게 보는 것은 일식을 볼 수 있는 지역이 좁아서 한 곳에서 자주 보기 힘들기 때문이다.

일식 중에서 가장 보기 힘든 개기일식은 최대 7분 30초를 넘지 못한다. 지구에 드리워지는 달의 그림자가 시속 1700km 이상의 속도로 움직이기 때문이다. 6분을 넘는 개기일식도 굉장히 드물다. 지난 7월 22일에 일어난 개기일식은 지속 시간이 최대 6분 이상으로 최근 일어난 개기일식 중에서 가장 길었다. 하지만 개기일식을 아주 오랫동안 감상할 수 있는 방법이 있다. 바로 비행기를 타고 구름 위로 올라가 달의 그림자를 따라가는 것! 그렇게 하면 장장 한 시간이 넘게 개기일식을 감상할 수 있다.
 

최소공배수로 일식의 주기를 알아낸다!

일식은 해와 달이 교점에서 15° 이내에서 만나는 날짜와 시간을 알면 예측할 수 있다. 옛날 사람들은 해와 달이 규칙적으로 움직인다는 사실을 이용해 그게 언제인지를 계산했다. 그 결과 일식이 일정한 주기로 일어난다는 사실을 발견했다.

해가 교점을 지난 뒤 다시 그 교점에 돌아오는 데는 약 346.6일이 걸린다. 달이 교점을 지난 뒤 다시 그 교점에 돌아오는 데는 약 27.212일이 걸린다. 그러면 해와 달이 교점에서 만난 뒤 다시 똑같은 교점에서 만나려면 시간이 얼마나 걸릴까? 346.6일과 27.212일의 최소공배수를 구하면 정답을 알 수 있다.

346.6일 × 19 = 6585.4일
27.212일 × 242 = 6585.3일

최소공배수를 구한 결과 약 6585일이 나왔다. 해와 달이 교점에서 만난 뒤 약 6585일이 지나면 다시 같은 교점에서 만난다.

즉, 지구의 어떤 장소에서 일식이 일어난 뒤 6585일이 지나면 같은 장소에서 똑같은 일식을 볼 수 있는 것이다. 그러나 실제로는 일식이 일어나는 장소가 바뀐다. 최소공배수가 정확히 6585일이 아니라 6585.3일 정도 되기 때문이다.

소수점 아래의 0.3또는 0.4일 때문에 일식은 24시간 × 0.3 또는 0.4 = 약 8시간 만큼 늦어진다. 그 동안 지구도 자전하므로 일식을 볼 수 있는 장소가 서쪽으로 움직이는 것이다. 8시간씩 늦어지는일이 3번 모이면 꼭 하루가 늦어지기 때문에 6585.3일이 3번 지나면 또다시 같은 장소에서 같은 일식을 볼 수 있다.

6585.3일을 환산하면 18년 11일 8시간이 되는데, 이것을 ‘사로스 주기’라고 한다. 사로스 주기는 고대 바빌로니아 시절부터 알려져 있었다. 사로스 주기에 따라 거의 똑같은 일식이 반복해서 일어나기 때문에 지금이 사로스 주기의 어느 때에 해당하는지를 알면 다음에 일식이 언제 일어날지를 예상할 수 있다.

고대 그리스의 수학자인 탈레스와 일식에 관한 일화는 유명하다. 메디아와 리디아라는 두 나라가 전쟁을 벌이고 있을 때 탈레스는 곧 일식이 일어난다고 예언했다. 얼마 뒤 예언이 적중해 정말로 일식이 일어나자 전쟁 중이던 두 나라는 신의 노여움을 살까 봐 전쟁을 멈추고 평화 협정을 맺었다고 한다.

이 이야기가 과연 사실일까? 현대의 과학자들은 컴퓨터로 과거의 일식을 계산한 결과 기원전 585년 5월 28일에 현재의 터키에서 개기일식이 일어났음을 밝혀냈다. 기록이 사실이라면 기원전 585년의 일식이 바로 탈레스가 예측한 일식일 가능성이 높다.
 

최소공배수 구하는 법 

최소공배수는 두 개의 정수가 있을 때 둘 모두의 배수가 되는 최소의 자연수를 말한다. 예를 들어, 4와 5의 최소공배수를 구해 보자.

▶4의 배수는
4, 8, 12, 16, 20, 24…

▶5의 배수는
5, 10, 15, 20, 25….

동시에 4와 5의 배수가 되는 가장 작은 수는 20이므로, 20이 4와 5의 최소공배수가 된다.

한편, 최대공약수는 두 개의 정수가 있을 때 둘 모두의 약수가 되는 최대의 자연수를 말한다.

▶12의 약수는 1, 2, 3, 4, 6
▶16의 약수는 1, 2, 4, 8

따라서 12와 16의 최대공약수는 4가 된다.

최소공배수는 최대공약수를 이용해 구할 수 있다. 두 정수를 곱한 뒤 최대공약수로 나누면 최소공배수가 된다. 12와16의 최소공배수를 구한다면 $\frac{12 X 16}{4}$가 되어 답은 48이 되는 것이다.


일식으로 역사의 기록을 검증한다

일식은 역사 연구에도 큰 도움이 된다. 일식 기록을 이용해 언제 일어났는지 잘 모르는 사건의 연도를 알아낼 수 있기 때문이다. 일식은 옛날부터 중요한 현상이어서 기록으로 남아 있는 경우가 많다. 이 기록과 현대의 컴퓨터로 계산한 과거의 일식 기록을 비교하면 몇 년도에 일어난 일식인지 알 수 있다. 이를 기준으로 과거에 일어났던 다른 사건의 연대를 확인하거나 새롭게 알아낼 수 있다.


조선의 일식 계산법, 칠정산

옛날 우리나라에서도 해와 달이 동시에 교점에 가까이 오는 때를 계산하는 방법으로 일식을 예측했다. 조선 시대 초기에는 중국에서 들여온 ‘선명력’과 ‘대통력’이라는 역법을 사용했는데, 일식은 선명력을 이용해 계산했다. 그러나 822년에 만들어진 선명력은 너무 오래 돼 조선 시대에는 잘 맞지 않았다.

세종대왕을 화나게 한 1422년의 일식 계산 실수도 중국의 역법을 들여오는 과정에서 생긴 오차 때문이었다. 이를 개선하기 위해 세종대왕은 이순지에게 여러 역법을 연구해 우리나라에 잘 맞는 역법을 만들도록 명했다. 그 결과 탄생한 것이 칠정산내편과 칠정산외편이다.

칠정산내편은 중국식 역법을 우리나라에 맞게 고쳐 만든 역법이다. 해와 달의 위치 변화가 표로 담겨 있어 이를 이용해 해와 달이 언제 같은 자리에 오는지 계산했다. 칠정산내편에서는 원의 중심각을 1년의 길이인 365.2425°로 정했기 때문에, 해가 움직인 각도가 하루에 1°가 돼 계산하기 편리했다.

반면에 칠정산외편은 2세기에 살았던 천문학자 프톨레마이오스의 천문학을 기초로 한 서양식 방법으로 일식을 계산하는 법을 담고 있다. 서양에서는 고대 바빌로니아의 영향을 받아 60진법을 사용했기 때문에 원의 중심각을 360°로 사용했다. 칠정산외편은 내편과 달리 기하학적인 모델도 이용했다. 프톨레마이오스가 만든 우주의 구조에 바탕을 둔 계산법을 이용했던 것이다.

일식을 정확하게 계산하기 위해서는 고도의 수학이 필요했다. 계산기나 컴퓨터가 없던 시절 천문 현상을 계산하는 관리들은 나뭇가지(산가지)와 같은 도구를 이용해 연립방정식, 제곱근, 삼각함수 등을 계산했다. 또한 칠정산내편과 외편으로 각각 계산한 결과를 비교해 보며 계산이 정확한지를 확인했다. 훗날 칠정산은 오차가 너무 커져 새로운 역법인 시헌력으로 바뀌었지만 150년 동안이나 일식 예측에 사용됐다.

일식과 같은 천문 현상을 설명하고 예측하기 위해서는 수학이 꼭 필요하다. 고대 바빌로니아의 사례로 알 수 있듯이 수학이 발달한 곳에서 천문학도 함께 발달했다. 우리 조상들도 뛰어난 수학 실력을 이용해 칠정산처럼 믿을 만한역법을 만들어 쓸 수 있었다. 이제 앞으로는 일식이나 월식과 같은 천문 현상을 관찰할 때도 신비로운 우주에 숨어 있는 명쾌한 수학의 원리를 떠올려 보자.