d라이브러리

축구 선수 데이비드 베컴과 농구 선수 마이클 조던은 둘 다 등번호가 소수인 23번이다. 소수는 영어로 프라임 넘버(prime number)라고 하는데, 프라임은 중요하다는 뜻도 있다. 그래서일까. 데이비드 베컴은 레알 마드리드에서 로스앤젤레스 갤럭시로 구단을 옮길 때도 프라임 넘버,
23번을 고수했다.

데이비드 베컴이 구단의 핵심 선수인 것처럼 소수는 수학에서 중요한 역할을 하고 있다. 소수는 2, 3, 5, 7, 11, 13, … 과 같이 1과 자기 자신으로만 나누어 떨어지는 수로, 자연수를 만드는 기본 재료가 된다. 소수만 있으면 소수의 곱으로 자연수부터 정수, 유리수, 실수, 복소수까지 만들 수 있다. 이렇듯 소수가 수학의 토대라는 점에서 소수를 원자에 비유할 수 있다. 마치 원자의 결합을 통해 분자가 만들어지고 이를 통해 우주의 물질이 생성되는 것과 비슷하다.

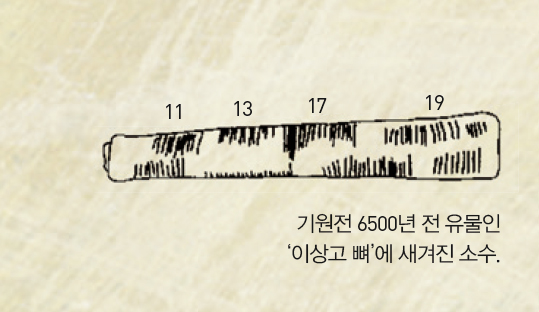
인류가 언제부터 소수에 대해 관심을 갖게 되었을까? 아주 멀리는 기원전 6500년경 유물인‘이상고 뼈(Isango bone)’에서 그 기원을 찾기도 한다. 이 뼈는 세 칸으로 나뉘어 있는데, 그 중 한칸에는 11, 13, 17, 19의 네 개의 수가 적혀 있다. 이는 10과 20 사이의 소수로, 수천 년 전 사람들이 이미 소수에 대한 지식을 가지고 있었다는 추측을 하게 만든다.

그리고 인류가 본격적으로 소수를 연구의 주제로 삼은 시기는 고대 그리스다. 기원전 300년경 수학자 유클리드는 이미 소수가 무한히 많다는 것을 증명했다. 이처럼 소수 연구는 아주 오래전부터 있었지만 여전히 많은 미해결 문제가 존재한다.





여전히 추측으로 남아 있는 골드바흐의 추측

유명한 미해결 문제 중 하나는 일본 추리소설 ‘용의자 X의 헌신’에도 나온 ‘골드바흐의 추측’이다. 명칭이 말하고 있듯이 ‘추측’일 뿐 아직 증명되지 못한 상태다. 골드바흐 추측은 ‘2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다’는 명제다.

간단하게 4=2+2, 6=3+3, 8=3+5와 같이 2보다 큰 짝수를 두 소수의 합으로 나타내볼 수 있다. 하지만 이처럼 특정 숫자를 직접 계산하는 것은 수학적 증명이 아니라 확인 작업일 뿐이다. 실제 4×1018까지의 짝수에 대해 이런 성질이 성립하는지는 확인했지만, 2보다 큰 ‘모든’ 짝수에
대해서 성립한다는 것을 완벽하게 증명하지는 못했다. 수학의 미해결 문제들은 대부분 문제를 이해하는 것조차 불가능할 정도로 난해하다. 하지만 골드바흐의 추측은 적어도 그 내용은 쉽게 이해할 수 있기 때문에 수학자가 아닌 일반인들도 많은 관심을 가지고 있다.

2보다 큰 짝수를 두 소수의 합으로 나타내는 방법은 하나 이상인 경우가 대부분이다. 이 때 방법의 개수를 ‘골드바흐의 수’라고 한다. 4부터 50까지의 짝수를 어떤 두 소수의 합으로 나타낼 수 있는지와 그에 따른 골드바흐의 수를 알아보면 다음과 같다.






암호 체계의 비밀을 지키는 열쇠, 리만 가설

아무도 증명하지 못한 것으로 유명한 소수 관련 난제가 또 있다. 독일의 수학자 베른하르트 리만이 1859년 발표한 ‘리만 가설’이다. 소수뿐만 아니라 수학 전체에서 가장 어려운 난제라고도 불린다.

수학에서 증명되지 못한 성질은 ‘골드바흐의 추측’, ‘케플러의 추측’과 같이 대개 ‘추측’이라고 한다. 그런데 리만 가설에는 추측이 아닌 ‘가설’이 붙어 있다. 일반적으로 가설은 어떤 이론을 세우는데 필수적인 가정인데, 리만 가설은 수학의 다양한 성질을 추론하는 기반이 되기 때문에 이렇게 부른다. 미국 클레이수학연구소는 이 문제에 100만 달러(약 11억 원)의 상금을 걸었으나 아직 아무도 상금을 받지 못했다.

사실, 리만 가설에 대한 증명은 고사하고 그 자체가 무엇인지를 이해하는 것조차도 쉽지 않다. 리만 가설이 무엇인지 설명하려면 리만제타함수의 정의부터 알아볼 필요가 있다. 리만제타함수란 다음과 같이 표현된다.




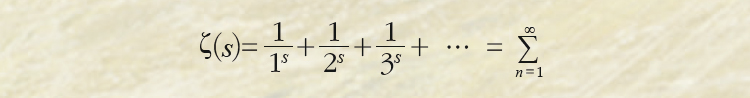
리만 가설은 리만제타함수 ζ(s)의 자명하지 않은 영점의 실수부가 모두 이라는 가설이다. 쉽게 말해서, 소수의 분포는 불규칙적이지만 소수로 표현되는 리만제타함수에는 어떤 규칙성이 있다는 것이다. 이 때문에 리만 가설을 증명할 경우 소수의 비밀이 상당 부분 밝혀질 수도 있다.






리만 가설은 영화 ‘뷰티플 마인드’에도 등장한다. 나중에 노벨경제학상을 받은 영화 주인공인 천재 수학자 존 내쉬(러셀 크로)는 젊은 시절 리만 가설의 증명에 몰두한다. 영화에서 내쉬는 리만 가설이 제기되고 100년째 되던 1959년 리만 가설에 대해 강연을 하게 되는데, 이 장면에서 말을 더듬으면서 비정상적인 모습을 보인다. 실제로 내쉬는 인터뷰에서 그 강연을 기점으로 정신이상이 시작됐다고 회고했다. 난해하기 그지없는 리만 가설은 내쉬를 조현병으로 몰고 간 주요 요인이었다.

소수는 현대의 전자상거래 등에 많이 쓰이는 공개키 암호를 만드는 기반이므로, 암호 보안 체계를 유지하는 열쇠와도 같다. 그런데 리만 가설이 해결되어 소수의 성질이 밝혀지면, 거대 소수의 목록이 공개되면서 암호 체계가 위협 받을 수도 있다. 이런 면에서 리만 가설의 증명은 독이 든 성배를 드는 것이고, 판도라의 상자를 여는 것에 비유되기도 한다.

AT&T나 휴렛패커드 같은 미국의 IT 회사들은 소수와 리만 가설의 연구에 막대한 연구비를 투자하고 있다. 인터넷 암호 체계가 언제 위태로워질지 그 시점을 알고 대비하기 위해서다.

소수는 중학교 1학년이면 배우는 간단한 개념이지만, 여전히 미해결 문제들이 많아서 수학자들의 학문적 호기심을 자극하곤 한다. 이런 호기심이 풍부한 연구로 이어지기 때문에 소수는 수학의 보물상자라고 할 수 있다.







박경미
홍익대 수학교육과에서 중·고등학생을 지도할 예비교사를 키우고 있다.
수학을 매개로 대중들과 소통하는 것이 가장 즐겁고, 그 다음은 테니스 칠 때이다.
베스트셀러 ‘수학비타민’ 작가이며, 교육현실 개선에도 큰 관심을 가지고 있다.
kpark@hongik.ac.kr