다각형 꼭짓점의 개수에서 전체 변의 개수를 빼고 면의 개수를 더한 값이 항상 일정하다는 오일러의 정리.
오일러의 정리는 세상에서 수없이 변하는 과정에도 결코 변치 않는 진리가 있다는 사실을 알려준다.
굴러 떨어지며 깎이고 깎이는 돌에서도 찾을 수 있는 수학의 진리를 만나보자.
당신은 3월 14일 하면 무엇이 떠오르는가? 사랑하는 연인에게 사탕을 선물하는 화이트데이? 아니면 원주율을 기념하는 파이데이? 만약 화이트데이 보다 파이데이를 먼저 떠올렸다면 당신은 수학과 무관한 사람은 아니다. 원주율을 기호 파이(π)로 나타내도록 대중화한 사람은 바로 스위스의 수학자 레온하르트 오일러였다. 파이에 얽힌 이야기는 많이 알려졌으니 이번에는 오일러의 다른 업적, ‘오일러의 정리’에 대해 알아보자.
오일러의 정리가 세상의 많은 현상을 수학적으로 설명한다는 사실을 알고 있는가. 흔하고 대수롭지 않은 자연 현상 속에서도 찾아볼 수 있다.
산 위에 있던 모난 돌덩이가 굴러 떨어지면서 시냇물에 씻기고 흘러 둥그스레한 모습으로 강가에 도달한다. 돌이 깎이고 깎이면서 모난 부분이 둥그렇게 변하는데, 한 곳에 몰린 모난 부분을 몸 전체로 나누는 과정으로 볼 수 있다. 수학적으로는 ‘돌 자신이 갖고 있는 뾰족한 정도의 합을 유지한다’고 표현한다. 쉽게 이해하기 위해 초등 수학으로 돌아가 보자.
모양 변해도 뾰족함의 합은 유지
초등학교나 중학교 때 배웠듯이 모든 다각형에서 외각의 합은 360°다. 삼각형에서 모서리를 잘라내 다른 다각형으로 만들어도 외각의 합은 항상 360°로 유지된다는 사실을 알 수 있다.
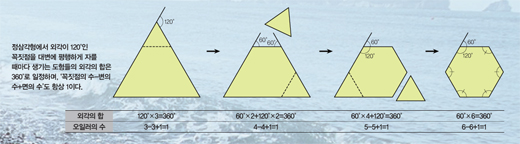
삼각형의 뾰족한 세 부분을 자를 때 어떤 일이 일어날까? 뾰족한 꼭짓점 1개를 잘라내면 덜 뾰족한 꼭짓점 2개가 생긴다. 꼭짓점이 뾰족하다는 것은 외각이 크다는 사실을 뜻한다. 정삼각형에서 외각이 120°인 꼭짓점 하나를 대변에 평행하게 자르면 외각이 각각 60°인 꼭짓점 두 개가 생긴다. 즉 뾰족함의 정도가 120인 부분이 잘리면서 뾰족함의 정도가 60인 부분 두 개로 나뉘었다는 얘기다.
결국 도형은 모양이 변하면서도 뾰족함의 합을 보존한다는 사실을 알 수 있다. 이런 현상은 3차원인 입체도형에서도 성립한다. 돌이 구르면서 모난 부분이 무뎌지는 과정은 한 곳에 몰린 모난 부분을 몸 전체가 나눠 갖는 과정, 즉 뾰족함의 합을 유지하는 과정이다.
이처럼 모든 도형의 외각 합이 360°라는 사실은 당연하면서도 대단히 놀랍다. 수학에서 가장 중요한 사실은 이렇게 ‘변하는 과정에서 결코 변치 않는 진리’를 찾는 일이다. 이것을 수학적 용어로 불변적인 성질, 즉 ‘불변량’(invariant)이라고 부른다.
다각형 꼭짓점의 개수를 v , 전체 변의 개수를 e, 면의 개수를 f 라고 하자 .
하나의 다각형에서 다른 다각형으로 계속 변화를 주는 데도 v -e +f =1의 값은 변하지 않는다. 이렇게 변하지 않는 v -e +f 의 값을 ‘오일러의 수’라 한다. 오일러는 꼭짓점의 개수, 모서리의 개수, 면의 개수 사이에 수학적으로 긴밀한 관계가 있음을 처음으로 밝힌 수학자다. 이것은 수학의 핵심영역 가운데 하나인 위상수학에서 첫 번째로 의미 있는 아이디어다.
정다면체가 5개뿐인 이유
다각형의 모양이 변하는 동안 서로 다른 불변량(외각의 합과 오일러의 수)이 존재하는 것 같지만 사실은 이 두 가지 불변량도 서로 연관돼 있다. 외각의 합과 오일러의 수 사이에는 다음과 같은 관계가 성립한다.
다각형 외각의 합 = (v-e+f)×360°=오일러의 수×360°
이 관계는 입체도형에서도 성립한다.
다면체 외각의 합 = (v-e+f)×360°=오일러의 수×360°
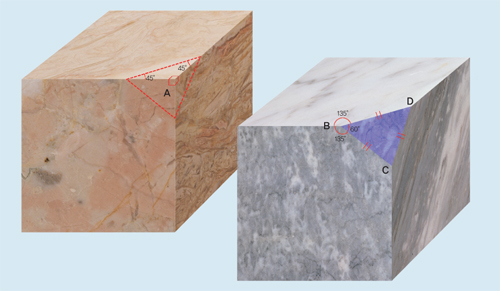
다면체에 있는 꼭짓점의 외각은 ‘360°-그 꼭짓점에 모인 면들의 내각의 합’으로 정의하며 다면체 외각의 합은 각 꼭짓점 외각들의 총합으로 정의한다. 정육면체의 경우 한 꼭짓점에 모인 면은 3개이며 내각은 90°, 외각은 360°-(3×90°), 즉 90°다.
만일 정육면체에서 외각이 90°인 꼭짓점 A가 잘리면 남아 있는 도형에 외각이 각각 30°인 세 개의 꼭짓점 B, C, D가 생긴다. 즉 뾰족함의 정도가 90인 부분이 잘리면서 뾰족함의 정도가 30인 세 부분으로 나뉜 것이다. 다면체도 모양이 변할 때 뾰족함의 합을 유지한다는 사실을 확인할 수 있다. 이때 오일러의 수를 계산하면 정육면체에서 꼭짓점 하나가 잘리기 전후 모두 v -e +f =2다. 실제 다면체의 오일러의 수는 언제나 2다. 또 다면체에서 외각의 합은 항상 2×360°=720°라는 사실을 추측할 수 있다.
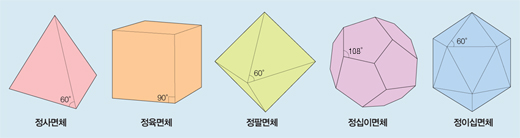
정육면체 이외의 다른 정다면체를 예로 들어보자. 정다면체는 5가지 종류밖에 존재하지 않는다. 먼저 정사면체 꼭짓점의 외각은 360°-3×60°=180°이고 합은 180°(한 꼭짓점의 외각)×4(꼭짓점의 개수)=720°다. 정팔면체(120°×6), 정십이면체(60°×12), 정이십면체(36°×20)도 외각의 합은 720°다. ‘구멍이 없는 모든 다면체’의 오일러의 수는 v -e +f =2, 외각의 합은 2×360°=720°로 일정하며 뾰족함의 합도 언제나 일정하다.
따라서 돌덩이는 산에서 굴러 떨어지는 동안 돌덩이에 구멍이 나지 않는 한 뾰족함의 합을 유지한다. 꼭짓점 개수, 모서리 개수, 면 개수의 관계인 오일러의 수를 유지하기 때문이다. 즉 자연은 수학 법칙에 의존하며 변화한다.
오일러의 수는 세상에 존재하는 정다면체가 왜 5개밖에 없는지에도 답을 준다. 정다면체에서 한 꼭짓점에 모이는 변 개수(P)와 한 면을 이루는 변 개수(Q), 그리고 오일러의 수를 이용하면 쉽게 증명된다. P와 꼭짓점 개수 v 를 곱해 2로 나누거나, Q와 면 개수 f 를 곱해 2로 나누면 전체 변 개수 e가 나온다(e=Pv/2=Qf/2). 여기서 v와 f를 각각 2e/P, 2e/Q로 정리해 오일러의 수 v -e +f =2에 대입하면
1/P + 1/Q = 1/2 + 1/e 로 1/P + 1/A 은 항상 1/2보다 크다는 결과가 나온다. 정다면체의 특성상 P와 Q는 3보다 크기 때문에 이 식을 만족하는 P와 Q는 (3,3) (3,4) (3,5) (4,3) (5,3) 5쌍밖에 없다. 결국 존재하는 정다면체는 각각 정사면체, 정육면체, 정십이면체, 정팔면체, 정이십면체인 5개뿐이다. 자세한 계산과정은 동아사이언스 홈페이지(www.dongaScience.com)에 실었다.
또 정오각형을 정육각형이 둘러싸고, 정육각형을 정오각형과 정육각형이 번갈아 둘러싸면서 만든 다면체가 정육각형 20개와 정오각형 12개로 이뤄진 32면체 축구공 모양인 이유도 오일러의 수가 2기 때문이다. 실제 자연에도 탄소 60개가 축구공 모양을 이룬 물질(C60)이 있는데, 바로 ‘풀러렌’(fullerene)이다.
4차원 도형에서 오일러의 수는?
 여러분은 4차원을 상상할 수 있는가. 4차원에 존재하는 도형의 오일러의 수는 얼마일까.
여러분은 4차원을 상상할 수 있는가. 4차원에 존재하는 도형의 오일러의 수는 얼마일까.
2차원 평면에서 도형을 직선으로 둘러싸려면 직선 3개가 필요하다. 마찬가지로 3차원 공간에서 2차원 평면으로 도형을 둘러싸려면 평면이 4개가 필요한데, 이는 바로 사면체다. 사면체에는 평면 3개가 모이는 꼭짓점이 총 4개가 있다. 모서리의 개수는 4개의 점에서 두 점을 선택하는 조합으로 구해 4C₂=6이고 면의 개수는 4개의 점에서 세 점을 선택하는 조합인 4C₃=4이므로 오일러의 수는 4-6+4=2다.
일반적으로 n차원 공간에 있는 도형에서 꼭짓점의 수를 v, 모서리의 수를 e, 2차원 면의 수를 f2, 3차원 면의 수를 f3, n차원 면의 수를 fn이라 할 때, 오일러의 수는 다음과 같이 정의한다.
이제 4차원 도형의 오일러의 수를 구해 보자. 2차원과 3차원에서 도형을 둘러싸는 원리를 고려해 4차원을 생각해 보면, 4차원 공간에서 도형을 둘러싸려 할 때 3차원 공간 5개가 필요하다는 사실을 유추할 수 있다. 따라서 이 도형은 4개의 3차원 공간이 만나는 교점인 꼭짓점이 5개이고, 모서리 개수는 5개의 점에서 두 점을 선택하는 경우의 수이므로 5C₂ =10이다. 또 면의 개수는 5개의 점에서 세 점을 선택하는 경우의 수이므로 5C₃=10이다. 또 3차원 면의 개수는 5개의 점에서 네 점을 선택하는 경우의 수이므로 5C₄=5이다. 결국 오일러의 수는 5-10+10-5=0이다. 실제로 이 도형처럼 구멍이 없는 모든 4차원 다면체(수학적으로 표현하면 연속적인 변화를 줘 4차원 구가 되는 도형)의 오일러의 수는 0이다.
5차원 도형은 어떠할까? 같은 방법으로 계산하면 오일러의 수는 6C₁-6C₂+6C₃-6C₄+6C4=2다. 6차원 도형은 7C₁-7C₂+7C₃-7C₄+7C5-7C6=0이다. 결국 차원이 높아지더라도 구멍이 없는 모든 n차원 다면체(연속적인 변화를 줘서 n차원의 구가 되는 도형)의 오일러의 수는 2와 0으로 반복된다고 예측할 수 있다.
이렇게 자연 속에 내재된 절대 변치 않는 이데아, 즉 수학이 자연 속에 존재하는 도형을 결정한다. 인간은 현상 속에 내재된 본질인 이데아를 생각할 수 있는 고귀한 존재다.
플라톤이 ‘아카데메이아’(Akademeia)를 개설하고 학교 현관에 “기하학을 모르는 자는 이 문 안에 들어오지 말라”라고 써 붙였다고 한다. 이때 플라톤이 생각한 기하학은 인간의 영혼을 더 높은 곳으로 향하게 하는 ‘이상’이었다. 오늘날 원칙이 사라진 가치관 속에서 살아가는 세대들이 3월 14일 파이데이를 맞아 순수한 본질을 되찾는 계기가 되길 바란다.
정삼각형에서 외각이 120°인 꼭짓점을 대변에 평행하게 자를 때마다 생기는 도형들의 외각의 합은 360°로 일정하며, ‘꼭짓점의 수-변의 수+면의 수’도 항상 1이다.
최영기 교수는 미국 로체스터대에서 위상수학으로 박사학위를 받았다.
현재 서울대 수학교육과 교수로 재직 중이고 서울대 과학영재센터 소장을 맡고 있다. 대수적 위상수학, 수학교육, 영재교육 분야를 연구하고 있다.
오일러의 정리는 세상에서 수없이 변하는 과정에도 결코 변치 않는 진리가 있다는 사실을 알려준다.
굴러 떨어지며 깎이고 깎이는 돌에서도 찾을 수 있는 수학의 진리를 만나보자.
당신은 3월 14일 하면 무엇이 떠오르는가? 사랑하는 연인에게 사탕을 선물하는 화이트데이? 아니면 원주율을 기념하는 파이데이? 만약 화이트데이 보다 파이데이를 먼저 떠올렸다면 당신은 수학과 무관한 사람은 아니다. 원주율을 기호 파이(π)로 나타내도록 대중화한 사람은 바로 스위스의 수학자 레온하르트 오일러였다. 파이에 얽힌 이야기는 많이 알려졌으니 이번에는 오일러의 다른 업적, ‘오일러의 정리’에 대해 알아보자.
오일러의 정리가 세상의 많은 현상을 수학적으로 설명한다는 사실을 알고 있는가. 흔하고 대수롭지 않은 자연 현상 속에서도 찾아볼 수 있다.
산 위에 있던 모난 돌덩이가 굴러 떨어지면서 시냇물에 씻기고 흘러 둥그스레한 모습으로 강가에 도달한다. 돌이 깎이고 깎이면서 모난 부분이 둥그렇게 변하는데, 한 곳에 몰린 모난 부분을 몸 전체로 나누는 과정으로 볼 수 있다. 수학적으로는 ‘돌 자신이 갖고 있는 뾰족한 정도의 합을 유지한다’고 표현한다. 쉽게 이해하기 위해 초등 수학으로 돌아가 보자.
모양 변해도 뾰족함의 합은 유지
초등학교나 중학교 때 배웠듯이 모든 다각형에서 외각의 합은 360°다. 삼각형에서 모서리를 잘라내 다른 다각형으로 만들어도 외각의 합은 항상 360°로 유지된다는 사실을 알 수 있다.
삼각형의 뾰족한 세 부분을 자를 때 어떤 일이 일어날까? 뾰족한 꼭짓점 1개를 잘라내면 덜 뾰족한 꼭짓점 2개가 생긴다. 꼭짓점이 뾰족하다는 것은 외각이 크다는 사실을 뜻한다. 정삼각형에서 외각이 120°인 꼭짓점 하나를 대변에 평행하게 자르면 외각이 각각 60°인 꼭짓점 두 개가 생긴다. 즉 뾰족함의 정도가 120인 부분이 잘리면서 뾰족함의 정도가 60인 부분 두 개로 나뉘었다는 얘기다.
결국 도형은 모양이 변하면서도 뾰족함의 합을 보존한다는 사실을 알 수 있다. 이런 현상은 3차원인 입체도형에서도 성립한다. 돌이 구르면서 모난 부분이 무뎌지는 과정은 한 곳에 몰린 모난 부분을 몸 전체가 나눠 갖는 과정, 즉 뾰족함의 합을 유지하는 과정이다.
이처럼 모든 도형의 외각 합이 360°라는 사실은 당연하면서도 대단히 놀랍다. 수학에서 가장 중요한 사실은 이렇게 ‘변하는 과정에서 결코 변치 않는 진리’를 찾는 일이다. 이것을 수학적 용어로 불변적인 성질, 즉 ‘불변량’(invariant)이라고 부른다.
다각형 꼭짓점의 개수를 v , 전체 변의 개수를 e, 면의 개수를 f 라고 하자 .
하나의 다각형에서 다른 다각형으로 계속 변화를 주는 데도 v -e +f =1의 값은 변하지 않는다. 이렇게 변하지 않는 v -e +f 의 값을 ‘오일러의 수’라 한다. 오일러는 꼭짓점의 개수, 모서리의 개수, 면의 개수 사이에 수학적으로 긴밀한 관계가 있음을 처음으로 밝힌 수학자다. 이것은 수학의 핵심영역 가운데 하나인 위상수학에서 첫 번째로 의미 있는 아이디어다.
정다면체가 5개뿐인 이유

다각형의 모양이 변하는 동안 서로 다른 불변량(외각의 합과 오일러의 수)이 존재하는 것 같지만 사실은 이 두 가지 불변량도 서로 연관돼 있다. 외각의 합과 오일러의 수 사이에는 다음과 같은 관계가 성립한다.
다각형 외각의 합 = (v-e+f)×360°=오일러의 수×360°
이 관계는 입체도형에서도 성립한다.
다면체 외각의 합 = (v-e+f)×360°=오일러의 수×360°
다면체에 있는 꼭짓점의 외각은 ‘360°-그 꼭짓점에 모인 면들의 내각의 합’으로 정의하며 다면체 외각의 합은 각 꼭짓점 외각들의 총합으로 정의한다. 정육면체의 경우 한 꼭짓점에 모인 면은 3개이며 내각은 90°, 외각은 360°-(3×90°), 즉 90°다.
만일 정육면체에서 외각이 90°인 꼭짓점 A가 잘리면 남아 있는 도형에 외각이 각각 30°인 세 개의 꼭짓점 B, C, D가 생긴다. 즉 뾰족함의 정도가 90인 부분이 잘리면서 뾰족함의 정도가 30인 세 부분으로 나뉜 것이다. 다면체도 모양이 변할 때 뾰족함의 합을 유지한다는 사실을 확인할 수 있다. 이때 오일러의 수를 계산하면 정육면체에서 꼭짓점 하나가 잘리기 전후 모두 v -e +f =2다. 실제 다면체의 오일러의 수는 언제나 2다. 또 다면체에서 외각의 합은 항상 2×360°=720°라는 사실을 추측할 수 있다.

정육면체 이외의 다른 정다면체를 예로 들어보자. 정다면체는 5가지 종류밖에 존재하지 않는다. 먼저 정사면체 꼭짓점의 외각은 360°-3×60°=180°이고 합은 180°(한 꼭짓점의 외각)×4(꼭짓점의 개수)=720°다. 정팔면체(120°×6), 정십이면체(60°×12), 정이십면체(36°×20)도 외각의 합은 720°다. ‘구멍이 없는 모든 다면체’의 오일러의 수는 v -e +f =2, 외각의 합은 2×360°=720°로 일정하며 뾰족함의 합도 언제나 일정하다.
따라서 돌덩이는 산에서 굴러 떨어지는 동안 돌덩이에 구멍이 나지 않는 한 뾰족함의 합을 유지한다. 꼭짓점 개수, 모서리 개수, 면 개수의 관계인 오일러의 수를 유지하기 때문이다. 즉 자연은 수학 법칙에 의존하며 변화한다.
오일러의 수는 세상에 존재하는 정다면체가 왜 5개밖에 없는지에도 답을 준다. 정다면체에서 한 꼭짓점에 모이는 변 개수(P)와 한 면을 이루는 변 개수(Q), 그리고 오일러의 수를 이용하면 쉽게 증명된다. P와 꼭짓점 개수 v 를 곱해 2로 나누거나, Q와 면 개수 f 를 곱해 2로 나누면 전체 변 개수 e가 나온다(e=Pv/2=Qf/2). 여기서 v와 f를 각각 2e/P, 2e/Q로 정리해 오일러의 수 v -e +f =2에 대입하면
1/P + 1/Q = 1/2 + 1/e 로 1/P + 1/A 은 항상 1/2보다 크다는 결과가 나온다. 정다면체의 특성상 P와 Q는 3보다 크기 때문에 이 식을 만족하는 P와 Q는 (3,3) (3,4) (3,5) (4,3) (5,3) 5쌍밖에 없다. 결국 존재하는 정다면체는 각각 정사면체, 정육면체, 정십이면체, 정팔면체, 정이십면체인 5개뿐이다. 자세한 계산과정은 동아사이언스 홈페이지(www.dongaScience.com)에 실었다.
또 정오각형을 정육각형이 둘러싸고, 정육각형을 정오각형과 정육각형이 번갈아 둘러싸면서 만든 다면체가 정육각형 20개와 정오각형 12개로 이뤄진 32면체 축구공 모양인 이유도 오일러의 수가 2기 때문이다. 실제 자연에도 탄소 60개가 축구공 모양을 이룬 물질(C60)이 있는데, 바로 ‘풀러렌’(fullerene)이다.
4차원 도형에서 오일러의 수는?
 여러분은 4차원을 상상할 수 있는가. 4차원에 존재하는 도형의 오일러의 수는 얼마일까.
여러분은 4차원을 상상할 수 있는가. 4차원에 존재하는 도형의 오일러의 수는 얼마일까.2차원 평면에서 도형을 직선으로 둘러싸려면 직선 3개가 필요하다. 마찬가지로 3차원 공간에서 2차원 평면으로 도형을 둘러싸려면 평면이 4개가 필요한데, 이는 바로 사면체다. 사면체에는 평면 3개가 모이는 꼭짓점이 총 4개가 있다. 모서리의 개수는 4개의 점에서 두 점을 선택하는 조합으로 구해 4C₂=6이고 면의 개수는 4개의 점에서 세 점을 선택하는 조합인 4C₃=4이므로 오일러의 수는 4-6+4=2다.
일반적으로 n차원 공간에 있는 도형에서 꼭짓점의 수를 v, 모서리의 수를 e, 2차원 면의 수를 f2, 3차원 면의 수를 f3, n차원 면의 수를 fn이라 할 때, 오일러의 수는 다음과 같이 정의한다.
이제 4차원 도형의 오일러의 수를 구해 보자. 2차원과 3차원에서 도형을 둘러싸는 원리를 고려해 4차원을 생각해 보면, 4차원 공간에서 도형을 둘러싸려 할 때 3차원 공간 5개가 필요하다는 사실을 유추할 수 있다. 따라서 이 도형은 4개의 3차원 공간이 만나는 교점인 꼭짓점이 5개이고, 모서리 개수는 5개의 점에서 두 점을 선택하는 경우의 수이므로 5C₂ =10이다. 또 면의 개수는 5개의 점에서 세 점을 선택하는 경우의 수이므로 5C₃=10이다. 또 3차원 면의 개수는 5개의 점에서 네 점을 선택하는 경우의 수이므로 5C₄=5이다. 결국 오일러의 수는 5-10+10-5=0이다. 실제로 이 도형처럼 구멍이 없는 모든 4차원 다면체(수학적으로 표현하면 연속적인 변화를 줘 4차원 구가 되는 도형)의 오일러의 수는 0이다.
5차원 도형은 어떠할까? 같은 방법으로 계산하면 오일러의 수는 6C₁-6C₂+6C₃-6C₄+6C4=2다. 6차원 도형은 7C₁-7C₂+7C₃-7C₄+7C5-7C6=0이다. 결국 차원이 높아지더라도 구멍이 없는 모든 n차원 다면체(연속적인 변화를 줘서 n차원의 구가 되는 도형)의 오일러의 수는 2와 0으로 반복된다고 예측할 수 있다.
이렇게 자연 속에 내재된 절대 변치 않는 이데아, 즉 수학이 자연 속에 존재하는 도형을 결정한다. 인간은 현상 속에 내재된 본질인 이데아를 생각할 수 있는 고귀한 존재다.
플라톤이 ‘아카데메이아’(Akademeia)를 개설하고 학교 현관에 “기하학을 모르는 자는 이 문 안에 들어오지 말라”라고 써 붙였다고 한다. 이때 플라톤이 생각한 기하학은 인간의 영혼을 더 높은 곳으로 향하게 하는 ‘이상’이었다. 오늘날 원칙이 사라진 가치관 속에서 살아가는 세대들이 3월 14일 파이데이를 맞아 순수한 본질을 되찾는 계기가 되길 바란다.
정삼각형에서 외각이 120°인 꼭짓점을 대변에 평행하게 자를 때마다 생기는 도형들의 외각의 합은 360°로 일정하며, ‘꼭짓점의 수-변의 수+면의 수’도 항상 1이다.
최영기 교수는 미국 로체스터대에서 위상수학으로 박사학위를 받았다.
현재 서울대 수학교육과 교수로 재직 중이고 서울대 과학영재센터 소장을 맡고 있다. 대수적 위상수학, 수학교육, 영재교육 분야를 연구하고 있다.