필자는 어렸을 때 시골에서 자랐다. 요즘 같은 겨울철에는 팽이치기, 연날리기, 자치기, 쥐불놀이, 윷놀이, 구슬치기, 깡통차기 같은 놀이를 즐기느라 시간 가는 줄 몰랐다. 그 중에서도 동네 큰 마당에 모여 즐겼던 윷놀이가 특히 기억에 남는다.요즘 학생들은 기나긴 겨울 방학 때 뭘 하며 시간을 보낼까. 밀린 수학공부 하느라 놀 시간 없다고? 아니면 컴퓨터 게임과 인터넷 서핑하느라 밖에서 윷놀이 같은 건 할 시간 없다고? 만약 두 가지 모두 해당된다면 잠깐 짬을 내 가족들과 윷판을 벌여보자.
가족들과 즐거운 시간을 보낼 수 있을 뿐만 아니라 수학의 모든 영역을 한 번에 공부할 수도 있다.
수와 연산
윷놀이의 규칙은 집합과 명제로
어떤 놀이든 제대로 즐기기 위해서는 준비물과 규칙이 필요하다. 윷놀이는 윷가락과 말판과 말, 그리고 윷놀이를 즐길 사람이 있어야 한다. 또 윷을 던져서 나온 패에 맞춰 말을 움직인다거나, 말을 모두 불러들이면 승리한다 같은 규칙이 있다.
수학이라는 놀이도 마찬가지다. 수학의 재료인 수와 기호가 있어야 하며 이들을 갖고 노는 규칙이 필요하다. 수학의 8가지 영역에서 이에 해당하는 영역이 바로 ‘수와 연산’ 단원이다. 윷놀이를 하기 앞서 윷놀이의 준비물과 규칙을 수학적으로 이해해보자.
윷놀이는 여러 명이 두 패로 나눠 하는 놀이다. 예를 들어 여섯 명을 두 패로 나눠 윷놀이를 한다고 하자. 이들 두 패를 각각 갑팀과 을팀이라 하면 윷놀이에 참가하는 인원을 원소로 갖는 집합을 전체집합 U라고 할 수 있고, 전체집합 U안에 두 패로 나뉜 ‘갑 집합’과 ‘을 집합’을 만들 수 있다.
윷놀이에서 반드시 필요한 네 개의 윷가락으로도 다양한 종류의 집합을 생각할 수 있다. 네 개의 윷가락 모임이라고 하면 ‘윷가락의 집합’이 되고, 윷가락을 던졌을 때 나올 수 있는 경우의 집합은 {도, 개, 걸, 윷, 모}다.
준비물이 제대로 갖춰졌으니 규칙을 점검하자. 윷을 던져 패가 도, 개, 걸, 윷, 모가 나오면 말을 각각 1칸에서 5칸까지 움직일 수 있다. 또 상대편 말을 잡으면 한 번 더 윷을 던질 수 있다. 이를 명제로 표시하면 다음과 같다.
예를 들어 윷놀이에서 p1→q1, p2→q2, r1→s 따위는 참인 명제지만, p1→q2나 q1→s는 참이 아니다. 이때 2칸을 움직이면 상대편 말을 잡는 상황이 왔다고 하자. 그러면 q2→r1 이라는 참인 명제가 추가된다. 이 경우 명제들은 삼단논법에 따라, p2→q2 이고, q2→r1이고, r1→s이므로 p2→s는 참이 된다. 즉 개가 나오면 한 번 더 윷을 던진다는 명제가 참이라는 뜻이다.
윷놀이에서 이기기 위해서는 윷을 던져 무엇이 나왔는가도 중요하지만, 말판에서 말들을 어떻게 움직일지 정하는 작전이 더 중요하다. 이런 과정은 명제의 참, 거짓을 판별하거나 참인 명제들을 이용해 새로운 참 명제를 발견하는 일이다.
문자와 식
말을 운용하는 방정식
윷놀이에서 항상 윷이나 모를 던져야 좋은 건 아니다. 경우에 따라서는 1칸 앞에 있는 말을 잡기 위해 도가 나와야 할 때도 있고, 지름길로 가는 방에 들기 위해 개가 나와야 할 때도 있다. 따라서 윷을 던지면 마음먹은 대로 패가 나오는 건 아니므로, 윷놀이에서 이기려면 체계적이며 논리적인 전략을 세워야 한다.예를 들어 갑팀이 먼저 윷가락을 던져 윷이 나왔다고 하자. 윷놀이 규칙에 따라 한 번 더 던질 기회가 주어져 개가 나왔다고 하자. 갑팀은 말 하나를 윷과 개에 해당하는 칸으로 전진시켰다. 그렇다면 을팀은 윷가락을 던져 무엇이 나와야 말판에 있는 상대 말을 잡을 수 있을까?
윷가락이 뒤집어지고 엎어지는 여러 경우 각각에 도, 개, 걸, 윷, 모 같은 이름을 붙이는 일은 수학에서 수 대신 문자를 사용하는 일과 같다. 이 상황을 방정식을 세워 풀어보자.
우선 갑팀의 말은 윷과 개가 나왔으므로 모두 6칸을 전진했다. 따라서 을팀도 6칸을 전진할 수 있어야 한다. 그런데 6칸을 전진하기 위해서는 적어도 2번 이상, 6번 이하를 던져야 한다. 윷가락을 i번째 던졌을 때 말이 전진할 수 있는 칸의 수를 xi라 하고 문자를 사용해 식으로 나타내면 모두 다섯 가지 방법이 있다.
그런데 말판에 을 팀이 잡을 수 있는 갑 팀의 말이 없으므로 을 팀은 반드시 윷이나 모가 한번 이상 나와야 한다. 위의 각 경우에서 윷이나 모가 나오는 경우는 x1+x2=6과 x1+x2+x3=6 두 가지 경우다. 하지만 x1+x2+x3=6의 (도 2번, 윷 1번)은 도를 연속해서 2번 움직일 수 없으므로, 가능한 경우는 x1+x2=6뿐이다.
x1+x2=6을 만족하는 방정식의 해를 순서쌍 (x1, x2)로 나타내면, (4,2), (2,4), (5,1), (1,5)다. 다시 말해 (윷, 개), (개, 윷), (모, 도), (도, 모)다. 이 가운데 윷이나 모가 먼저 나와야 한 번 더 던질 수 있으므로, 가능한 해는 (윷, 개), (모, 도)밖에 없다.
그런데 여기서 조건 하나가 더 붙는다. 모가 먼저 나오면 말판에서 첫 번째 지름길로 가는 방에 도착해 진로가 달라지므로 앞의 말을 잡을 수 없다. 결국 방정식의 해는 (윷, 개) 하나뿐이다.
윷놀이를 할 때 실제로 이런 방정식을 풀어서 말을 운용하는 사람은 없겠지만, 사실 우리 머릿속에서는 이 같은 수학적인 과정이 이뤄지고 있다.
기하
윷가락의 기하학
준비물과 규칙, 그리고 전략을 세웠으니, 이제 윷가락을 던질 차례다. 4개의 윷가락은 한 손에 가지런히 세워 쥔 뒤 멍석 위로 신명나게 던지기… 전에, 잠깐! 윷가락을 자세히 살펴보자.
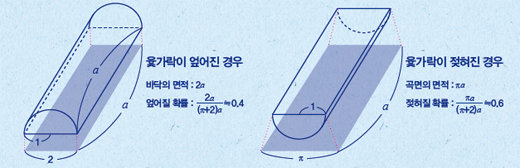
윷가락은 단면이 직사각형이고, 끝 부분이 반원인 반쪽짜리 원기둥이다. 윷가락을 만들 때 무엇보다 중요한 일은 각각의 윷가락이 엎어지거나 젖혀지는 확률이 같아야 한다는 점이다. 그러려면 원기둥의 밑면에 있는 원의 지름을 정확하게 찾아서 원을 이등분해 각각의 윷가락의 겉넓이를 모두 같게 해야 한다.
윷가락 원기둥의 반지름 길이가 1이고, 높이는 a라고 하자. 그러면 윷가락 단면 직사각형의 세로 길이는 2, 가로 길이는 a이므로 넓이는 2a이다. 한편 곡면을 넓게 펴면 세로 길이는 반지름 길이가 1인 반원의 둘레 길이와 같으므로 π이고, 가로의 길이가 a인 직사각형이 된다. 따라서 넓이는 πa다.
윷을 던졌을 때 윷가락이 젖혀지는 경우는 윷가락의 곡면이 바닥에 붙을 경우이고, 엎어지는 경우는 평면이 바닥에 붙는 경우다. 따라서 젖혀지는 경우의 확률은 전체 넓이에 대한 곡면의 넓이이므로 π/π+2≒0.6이고, 엎어지는 경우는 전체 넓이에 대한 평면의 넓이이므로 2/π+2≒0.4다. 이 확률을 이용하면 윷놀이에서 도, 개, 걸, 윷, 모가 나오는 확률을 구할 수 있다.
확률과 통계
도를 복돼지라 부르는 이유
윷놀이에서 각 표가 나오는 확률을 구해보자. 먼저 도가 나오는 경우는 한 개의 윷가락이 젖혀지고 나머지는 엎어지는 경우이므로 4개의 윷가락에서 1개를 선택하는 것과 같다. 즉 4가지가 가능해 도가 나올 확률은 (0.4×0.4×0.4×0.6)×4=0.1536이다.
개가 나오는 경우는 두 개의 윷가락이 엎어지고 두 개의 윷가락이 젖혀지는 경우이므로 4개 중에서 2개를 선택하는 것과 같다. 즉 6가지다. 따라서 개가 나올 확률은 (0.4×0.4×0.6×0.6)×6=0.3456이다. 마찬가지로 걸, 윷, 모가 나올 확률을 각각 구하면 아래와 같다.
걸이 나올 확률 : (0.4×0.6×0.6×0.6)×4=0.3456
윷이 나올 확률 : (0.6×0.6×0.6×0.6)×1=0.1296
모가 나올 확률 : (0.4×0.4×0.4×0.4)×1=0.0256
실제로 윷을 수없이 던지면 도, 개, 걸, 윷, 모가 앞에서 구한 확률과 거의 비슷하게 나온다. 여러 패 가운데 특히 도를 ‘복돼지’라고 부르는데, 도가 나올 확률이 윷이 나올 확률과 거의 같기 때문이다.
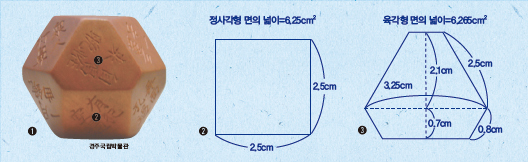
윷놀이 말고도 우리 조상들이 즐기던 목제주령구(木製酒令具)라고 부르는 일종의 주사위가 있다. 목제주령구는 신라시대 귀족들이 술자리에서 던진 뒤 나온 각 면에 쓰여 있는 벌칙을 주는 데 사용했던 놀이기구로, 중국이나 일본 등 동양에서는 물론 서양에서도 유례가 없는 독특한 놀이기구다.
목제주령구는 높이가 4.8㎝로 손에 딱 잡히는 크기인데 여느 주사위와는 달리 모양이 정육면체가 아니라 6개면은 정사각형, 8개면은 육각형인 14면체다.
놀라운 점은 14면체인 이 주사위를 던지면 정다면체가 아님에도 불구하고 각 면이 나올 확률이 거의 같다는 사실이다. 정다면체는 정4면체, 정6면체, 정8면체, 정12면체, 정20면체의 5개만이 수학적으로 가능하다. 정다면체가 불가능한 14면체의 각 면의 넓이를 거의 비슷하게 만들어 각 면이 나올 확률도 비슷하게 만든 것으로 보아 신라인의 수학 수준을 가늠할 수 있다.
함수
‘윷함수’를 말판이라는 좌표평면에 그린다?!
“윷이야~! 모야~!”
기대를 담아 신명나게 던진 윷가락은 허공을 가르며 몇 바퀴를 돌다가 멍석 위에 떨어진다. 윷가락은 멍석 위에서 몇 번 튀어 오르고, 윷가락끼리 부딪치며 구르다가 허연 배를 내놓고 뒤집히거나 볼록 엎드리기도 한다.
윷놀이에서 윷을 던져 나오는 모양과 전진할 수 있는 칸 수의 관계는 함수다. 이 함수를 ‘윷함수’라 하고 f(x)라 정의하면 윷함수 y= f(x)의 정의역은 X={도, 개, 걸, 윷, 모}이고, 공역은 Y={1,2,3,4,5}다. 윷 함수 y= f(x)는 공역과 치역이 일치하므로 일대일 대응함수이며 따라서 역함수도 정의되는, 수학적으로는 쓸모가 많은 함수다.
윷함수를 그래프로 그릴 수도 있을까. 정의역이 X이고, 공역이 Y인 함수 y= f(x)가 주어졌을 때, 정의역의 원소 a와 그것에 대응하는 함수값 f(a) 전체의 집합 G(f)={(a, f(a))|a∈X, f(a) ∈Y}를 함수 f의 그래프라고 한다.
그래프의 정의로부터 이 그래프는 곱집합 X×Y의 부분집합임을 알 수 있는데, 함수의 그래프를 그리는 일은 결국 평면좌표에서 전체 평면에 대한 부분집합을 찾는 문제와 같다.
함수의 그래프를 그리기 위해서 정의역의 한 원소와 그에 해당하는 함수값을 순서쌍 (a, f(a))로 나타낸다. 윷놀이에서는 (나온 윷의 모양, 말을 이동시키는 거리) 같이 순서쌍을 정할 수 있다. 그러면 (도, 1), (개, 2), (걸, 3), (윷, 4), (모, 5) 같은 순서쌍이 만들어진다.
다른 점이 있다면 함수의 그래프는 좌표평면 위에 그리는 것이고, 윷놀이에서는 말판 위에서 말이 이동한 경로를 나타낸다는 점뿐이다. 즉 윷놀이는 윷함수를 말판이라는 좌표평면에 그대로 그리는 수학놀이인 셈이다.
행렬과 그래프
윷놀이 말판을 행렬로!
윷놀이 말판이라는 좌표평면에 그리는 윷함수는 행렬로도 표현할 수 있다. 사실 행렬은 그래프와 표리일체로 모든 그래프는 행렬로 표현할 수 있다. 29개의 방이 있는 윷놀이 말판을 편의상 5개의 꼭지점이 있는 그래프 G라 하고 이를 행렬 A(G)로 나타내보자.
각 꼭지점에 번호를 정하고 행렬의 각 성분은 한 꼭지점에서 다른 꼭지점으로 직접 연결돼있으면 1, 그렇지 않다면 0이라고 하자. 예를 들어 A(G)의 (1,2)의 성분은 꼭지점 1과 2가 직접 연결돼 있으므로 1이고, (1,1)이나 (1, 4)처럼 서로 직접 연결된 선이 없는 경우는 0이다.
이렇게 정의된 행렬식 A(G)로 말이 한 방에서 다른 방으로 갈 수 있는 경로의 수를 구할 수 있다. 예를 들어 1번 방에 있는 말을 두 번 옮겨 갈 수 있는 방은 어느 곳이며, 그 방법은 몇 가지인지 알아보자.
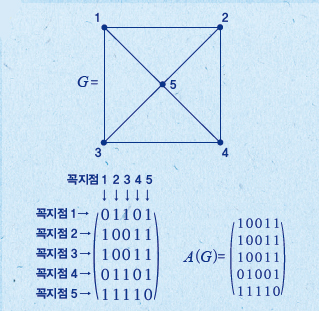
1번 방에 있는 말은 2번 만에 모든 방에 다 갈 수 있다. 이를테면 1번 방에 있는 말은 2번 만에 2번 방으로 갈 수 있고 그 방법은 1→5→2로 1가지다. 또 2번 방에 있는 말은 2번 만에 3번 방으로 갈 수 있고, 그 방법은 2→1→3, 2→5→3, 2→4→3의 3가지다.
이와 같은 문제를 그래프로 해결하기 위해서는 일일이 그래프를 그려 확인해야 한다. 하지만 행렬을 이용하면 매우 간단하게 모든 경우의 수를 찾을 수 있다. 말이 2번 움직여 갈 수 있는 곳을 찾기 위해 앞에서 구한 행렬 A를 2번 곱하면 구할 수 있는데, 이를 계산하면 아래와 같다.
이 행렬을 이용하면 1번 방에 있는 말을 2번 옮겨 다시 1번 방으로 오는 경우의 수(1,1)는 3이다. 또 3번 방에 있는 말을 2번 옮겨 2번 방으로 갈 수 있는 경우의 수(3,2)는 3이다. 같은 원리로 어떤 방에 있는 말이든지 10번 만에 다른 방으로 옮겨갈 수 있는 경우의 수는 행렬 A를 10제곱하면 된다.
이처럼 행렬은 점과 선으로 연결된 인터넷의 네트워크, 지하철이나 버스 같은 대중교통의 노선도를 그리는 데 수학적 방법으로 사용되고 있다.
지수와 로그
모든 경우의 수는 229가지
실제 윷놀이 말판에는 모두 29개의 방이 있다. 말 하나가 말판에 등장한 뒤 가장 짧게는 윷을 단 3번(모, 걸, 윷) 던져 다시 골인 지점으로 돌아올 수도 있고, 도만 계속 던진다면 윷가락을 21번 던질 수도 있다. 과연 하나의 말이 말판에 있는 방을 돌아 나올 수 있는 경우는 몇 가지나 될까?
여기에서는 문제를 간단히 하기 위해 말이 각 방에 들어가는 경우와 들어가지 않는 경우로만 나눠 생각하자. 윷놀이 말판의 29개 방에 말이 놓이거나 지나치게 될 경우의 수를 구하자는 뜻이다. 각 방에는 말이 놓이는 경우와 놓이지 않는 2가지 경우가 있고, 방은 모두 29개이므로 모든 경우의 수는 2를 29번 곱하는 것과 같다.
똑같은 2를 29번씩이나 쓰는 것은 매우 번거롭고 귀찮은 일이므로 이를 간단히 나타내기 위해 거듭제곱을 사용한다. 즉 2를 29번 곱하는 것은 229와 같이 나타낸다. 여기서 2를 밑, 29를 지수라고 한다.
그런데 윷놀이에는 모두 4개의 말이 있다고 했으므로 지수의 성질을 이용해 우리가 생각하는 모든 경우의 수를 구하면 4×229=22×229=231=2147483648이다.
즉 윷놀이에서 모든 말이 말판에 있는 방을 지나서 나올 수 있는 경우의 수는 2147483648가지다. 따라서 윷놀이에서 이기려면 2147483648가지 중에서 가장 좋은 방법을 택해야 한다.
미분과 적분
궁극의 윷놀이 불패 전법?
윷가락을 던지는 뛰어난 손놀림과 말을 운용하는 훌륭한 작전! 윷놀이에서 승리하는 핵심 요소다. 앞에서 다룬 수학의 모든 영역을 총동원해 윷놀이 불패 작전을 만들 수는 없을까. 만약 이런 작전이 존재한다면 꼭 들어가야 할 가장 중요한 수학의 기술이 있다. 바로 미분과 적분이다.
윷놀이에서 윷가락을 던질 때 윷가락은 곡선을 그리며 떨어진다. 따라서 윷가락이 매 순간 어떻게 움직일 것인가를 알고 싶다면 미분을 이용해야 한다. 실제로 윷가락을 던져 바닥에 떨어질 때까지 윷가락의 움직임을 그래프로 그리면 위로 볼록한 포물선이 된다. 이 포물선에 미분을 적용하면 윷가락을 던졌을 때 최대 높이나 윷가락이 바닥에 떨어질 때까지 걸린 시간도 구할 수 있다. 예를 들어 윷가락이 그리는 포물선은 이차함수로 표현된다. 이차함수와 미분을 이용하면 윷가락의 진로도 예상할 수 있다.
만약 윷을 던지는 힘과 각도를 함수로 표현하고 이를 계산할 수 있는 슈퍼컴퓨터가 내장된 로봇이 있다면, 아마 이 로봇은 미분과 적분을 이용해 윷가락을 어느 높이로 얼마만큼의 힘으로 던지면 원하는 패가 나올 수 있을 것인가를 계산한 뒤 정확하게 힘과 각도를 조절해 던질 것이다. 이뿐만 아니라 로봇은 바닥의 재질이나 탄성 등과 같은 물리적인 성질도 조사해 윷이 어떻게 튀는지도 예측할 것이다.
앞으로 이런 SF소설 같은 일이 실제로 일어날 수 있을지 장담할 수 없지만, 이와 비슷한 일이 실제로 일어나고 있다. 이를테면 지구 주위를 도는 인공위성이나 비행하는 물체를 추적하는 유도 미사일의 궤적은 미적분을 이용해 계산한다.
이광연 교수는 성균관대 수학과를 졸업하고 동대학원에서 석사와 박사학위를 받았다. 그뒤 미국 와이오밍주립대에서 박사후연구원을, 아이오와대에서 방문교수를 지냈다. 현재 한서대 수학과 교수로 재직 중이며, ‘웃기는 수학이지 뭐야’ ‘신화 속 수학이야기’ 같은 책을 펴냈다.
