d라이브러리

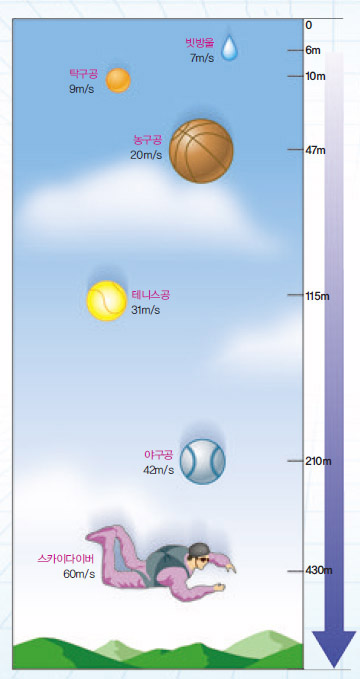
이 번 여름에는 소나기가 유난히 잦았다. 소나기는 약 5km 높이의 구름에서 떨어진다. 만약 소나기가 진공 속에서 떨어진다면 땅에 닿을 때 빗방울의 속도가 초속 200m를 넘을 것이다. 이 정도면 비를 맞으며 낭만을 찾기는커녕 목숨을 걸고 총알 같은 빗속을 뚫고 지나가야 한다. 하지만 실제로는 그렇지 않다. 비를 맞 으면 옷이 젖어 귀찮을 뿐 위험하지는 않다. 왜 그럴까.


소나기 맞아도 안죽는 이유

고양이는 높은 곳에서 떨어져도 잘 다치지 않는다. 스키선수는 비탈을 내려올 때 달걀 모양으로 몸을 한껏 움츠려서 속도를 높인다. 이는 모두 공기라는 유체속에서 물체가 유체와 다른 속도로 움직일 때 일어나는 현상이다.

유선형이 아닌 물체가 공기 중에서 빠른 속도로 움직이면 물체의 뒷부분에 소용돌이 모양의 공기 흐름이 생긴다. 이에 따라 물체에는 물체의 운동을 방해하는 방향으로‘끌림힘’(drag force)이 생긴다. 소나기와 높은 곳에서 떨어지는 고양이의 속도, 스키선수가 몸 을 움츠리는 이유는 끌림힘으로 설명할 수 있다.

끌림힘은 실험으로 얻은 결과에 따라 $D = \frac{1}{2}{C}_{ρ}A{v}^{2}$로 표현한다. 여기서 $ρ$는 공기의 밀도를, $A$는 속도에 수직인 방향의 단면적을, $v$는 물체의 속도를 나타낸다. $C$는 끌림계수라고 부르며 차원이 없는 양이다. 물체에 따라 다르지만 이 값은 보통 0.4~1.0이다.

빗방울은 떨어지는 동안 계속해서 중력을 받는데, 처음에 정지해있다가 떨어지면서 속도가 빨라질수록 중력과 반대방향으로 작용하는 끌림힘이 점점 커진다. 따라서 빗방울이 어느 정도 떨어지다 보면 빗방울에 작용하는 중력과 끌림힘의 크기가 같아지는 순간에 도달한다. 그러면 이때부터 빗방울은 일정한 속도로 떨어 진다. 이 속도를‘최종속도’라고 한다.

빗방울의 질량을 $m$, 중력가속도를 $g$라고 하면 빗방울이 최종속도에 도달했을 때 $\frac{1}{2}{C}_{ρ}A{{v}_{f}}^{2} = mg$이므로 최종속도 ${v}_{f} = \sqrt{\frac{2mg}{{C}_{ρ}A}}$ 다. 빗방울의 경우 약 6m 떨어지면 최종속도인 7m/s에 다다르고, 땅에 떨어질 때까지 계속 이 속도로 떨어진다. 결국 사람이 소나기를 맞아도 위험하지 않은 이유는 끌림힘으로 빗방울의 속도가 줄어들기 때문이다.

목숨 구한 독수리 자세

최종속도의 식을 보면 물체의 질량과 넓이, 끌림계수에 따라 최종속도가 달라진다는 사실을 알 수 있다. 물체가 무거울수록 최종속도는 커진다. 최종속도에 도달할 때까지 움직인 거리도 늘어난다. 예를 들어 농구공은 47m를 떨어져야 최종속도인 20m/s가 되고, 스카이다이버는 430m를 낙하해야 최종속도인 60m/s가 된다.

이런 식으로 계산하면 고양이는 6층 이상의 높이(약20m)에서 떨어져야 최종속도를 얻을 수 있다. 최종속도에 이르기 전까지는 끌림힘보다 중력이 크므로 아래로 가속된다. 우리 몸은 가속도(속도의 변화)는 잘 느끼지만 속도는 느끼지 못한다. 예를 들어 엘리베이터가 움직이기 시작할 때와 정지할 때만 엘리베이터가 움직인다고 느끼고, 그 사이 엘리베이터가 일정한 속도로 움
직일 때는 엘리베이터가 움직이는지 모른다.

고양이도 사람과 마찬가지다. 고양이가 높은 곳에서 떨어지기 시작할 때는 가속도를 느껴서 겁을 먹고 몸을 움츠리게 된다. 이는 넓이 A가 작아지는 것이므로 고양이의 최종속도는 더 커져서 이대로 떨어지면 다칠것이다. 하지만 최종속도에 도달하면 고양이는 마음이 편해져서 몸을 쭉 펴고 이로 인해 넓이가 커지므로 최종속도가 줄어든다. 그리고 땅에 가까이 오면 착지할 준비를 하고 땅에 안전하게 발을 디딘다.

스카이다이버들이 서로 손을 잡고 원을 그리며 내려올 때 팔과 다리를 쭉 편 자세로 있는 것도 같은 이유다. 다른 사람의 손을 잡아야하는데 상대방이 빨리 내려오고 있으면 손을 잡기가 어렵다. 따라서 되도록 속도를 늦춰야 한다.

그렇게 할 수 있는 유일한 방법은 공기와 부딪치는 면적을 가능한 넓혀 끌림힘을 최대한 크게 만드는 것이다. 그래서 팔과 다리를 쭉 편다. 이 자세는 마치 독수리가 날개를 펴고 있는 모양과 같다.

실제로 1987년 4월 스카이다이버인 그레고리 로버슨 씨는 끌림힘을 이용해 동료의 목숨을 구하기도 했다. 당시 로버슨 씨는 동료 스카이다이버가 다른 사람과 충돌해 정신을 잃고 떨어지는 장면을 목격했다. 로버슨 씨는 의식을 잃은 동료보다 훨씬 위에 있었고, 아직 낙하산을 펴지 않은 상태였다. 그는 머리를 아래로해서 공기와 부딪치는 단면적을 줄여서 속도를 높였다.

최종속도가 약 320km/h가 됐을 때 그는 동료가 있는 지점에 도달했고, 이후 독수리 자세를 취하고 속도를 줄여 동료를 붙잡았다. 그리고 동료의 낙하산을 펼친 뒤 자신은 바닥과 충돌하기 10초 전에 낙하산을 펼쳤다. 의식을 잃었던 동료는 땅에 닿기 직전 몸을 조절할 수 없었기 때문에 심하게 다쳤지만 다행히 목숨은 건질 수 있었다.

스키선수는 스카이다이버와 반대다. 되도록 끌림힘을 줄여야 재빨리 비탈을 내려올 수 있다. 끌림힘을 덜받으려면 공기와 부딪치는 단면적을 줄이면 된다. 그래서 고안된 자세가 달걀모양이다. 스키선수의 달걀모양은 결코 멋있게 보이려는 것이 아니라 과학적인 이유가 있는 것이다.
 

차원분석 아시나요

그렇다면 최종속도가 $\frac{1}{2}{C}_{ρ}A{v}^{2}$으로 표현되는 이유가 뭘까. 물체가 공기 속에서 움직이면 공기 분자들이계속 물체에 부딪친다. 그러면 물체는 공기분자로부터 운동량을 전달받는다. 따라서 단위시간당 공기분자가 전달하는 운동량이 바로 물체가 받는 끌림힘이 된다. 공기분자와 많이 충돌할수록 물체의 끌림힘은 커지므로 단위부피당 공기분자가 많을수록(즉 밀도가 클수록), 공기가 물체에 부딪치는 면적이 넓을수록 그리고 물체가 빠를수록 끌림힘은 커진다.

그런데 왜 하필이면 끌림힘은 밀도와 넓이에는 단순비례하고 속도는 그 제곱에 비례하는 것일까? 밀도의 제곱에 비례하고 속도에 비례하면 안되는 것일까?

차원분석을 이용하면 이를 쉽게 설명할 수 있다. 끌림힘에 영향을 주는 요소는 밀도, 넓이, 속도다. 끌림힘을 $D = {{C}_{ρ}}^{x}{A}^{y}{v}^{z}$의 일반적인 형태로 놓자. 여기서 $C$는 차원이 없는 상수이고, $x$, $y$, $z$는 우리가 결정해야 할 지수다.

차원이란 물체의 위치를 표시하는 독립적인 좌표의 개수를 말하기도 하지만(예를 들어 우리는 3차원 공간에서 살고 있다), 물리학에서는 물리량을 길이($L$), 질량($M$), 시간($T$)의 기본단위의 멱수로 표시하고, 이를 이 물리량의 차원이라고 하며 괄호 안에 넣어 표시한다.

예를 들어 밀도는 단위부피당 질량이므로 밀도의 차원 $[ρ] = M{L}^{-3}$ 이다. 넓이 $[A] = {L}^{2}$이될것이다. 속도는 단위시간당 움직인 거리이므로 속도의 차원 $[v] = L{T}^{-1}$이다. 차원이 없는 숫자란 $[c] = {L}^{0}{M}^{0}{T}^{0}$인경우를 말한다.

힘은 질량과 가속도의 곱이므로 힘의 차원은 $[D] = ML{T}^{-2}$이다. $D = {{C}_{ρ}}^{x}{A}^{y}{v}^{z}$에서 $ML{T}^{-2} = {(M{L}^{-3})}^{x}{({L}^{2})}^{y}{(L{T}^{-1})}^{z}$을 만족해야 한다. 여기서 양변의 $M$, $L$, $T$의 지수가 같다고 놓으면, $1=x$, $1=-3x+2y+z$, $-2=-z$이므로 $x=1$, $y=1$, $z=2$가 나온다. 따라서 끌림힘 $\frac{1}{2}{C}_{ρ}A{v}^{2}$이된다. 단 차원이 없는 계수 $c$는 $\frac{1}{2}C$로 놓았다.

차원분석은 매우 편리한 방법이어서 물리량을 구할때 많이 사용한다. 하지만 차원이 없는 계수에 대한 정보는 전혀 알 수 없다는 흠이 있다. 이 계수는 실제로 물리적인 운동방정식을 풀어야 구할 수 있다. 차원분석을 하고나니 머리는 복잡해졌겠지만 마음은 편해졌을 것이다.